このページでは、高校数学程度の行列の知識のうち、特定の種類の行列の呼び名について説明します。
数学で言う行列の定義と行列の演算(足し算、引き算、掛け算)については別途にまとめています。
行列は、行と列の数がそろっているものに限りませんが、多くの行列の用語は行と列の数が等しい正方行列に対してのものが多いです。そのため、このページで扱う行列の多くは正方行列になります。
$$例:3次の正方行列\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) $$
★ 正方行列の行の数(=列の数)をnとする時、その正方行列をn次の正方行列と呼ぶ事があります。例えば3×3行列は、3次の正方行列です。
★ 行列の中の各数値等を成分と言い、m行n列目の箇所にある成分を(m,n)成分などと言ったりします。
単位行列・零行列・対角行列
ここでは、行列は正方行列とします。
まずは簡単なものから見ていきましょう。
■ 単位行列 ■ 零行列(ゼロ行列) ■ 対角行列
■ 参考:虚数単位の行列表現

単位行列
まず、これは簡単です。ある行列Aに掛け算をした時に、掛け算の結果がAそのものになる行列を単位行列と言います。通常の掛け算で言う1に相当します。
★ 多くの場合、単位行列はIかEで表します。
行列の掛け算を行えるとき、A×I=I×A=Aが成立します。
一応ちょっとした注意点として、「行列の掛け算の定義」を何かてきとうに考えた時に、そのような「単位行列」の存在は必ずしも自明とは言えません。そのような行列が存在する事を示しておく必要があります。
もっとも、そのような単位行列は確かに存在し、次のようなものです。
$$例:3次の単位行列 I=\left(\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right) $$
このように、正方行列の「対角線」に相当するところ(これを対角成分と言います)が全て1であり、残りの成分は全て0である行列が単位行列です。何次の正方行列であっても、単位行列は「対角成分が全て1で、残りの成分は全て0」である行列として表せます。
簡単な計算例を見てみましょう。
$$\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) \left(\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right) $$
$$= \left(\begin{array}{ccc}
a_{11} \cdot 1+ a_{12} \cdot 0 + a_{13} \cdot 0& a_{11} \cdot 0+ a_{12} \cdot 1 + a_{13} \cdot 0 & a_{11} \cdot 0+ a_{12} \cdot 0 + a_{13} \cdot 1 \\
a_{21} \cdot 1+ a_{22} \cdot 0 + a_{23} \cdot 0 & a_{21} \cdot 0+ a_{22} \cdot 1 + a_{23} \cdot 0 & a_{21} \cdot 0+ a_{22} \cdot 0 + a_{23} \cdot 1 \\ a_{31} \cdot 1+ a_{32} \cdot 0 + a_{33} \cdot 0 & a_{31} \cdot 0+ a_{32} \cdot 1 + a_{33} \cdot 0 & a_{31} \cdot 0+ a_{32} \cdot 0 + a_{33} \cdot 1 \end{array}\right) $$
$$= \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) $$
掛け算の順番を入れ替えてI×Aを計算しても同様の結果になります。
一般の行列の掛け算では、A×Bは、ものによってB×Aに等しくなる事もあるし、等しくない事もあります。
零行列(ゼロ行列)
零行列とは、行列の全ての要素が0である行列です。これは正方行列でなくてもそのような行列は当然あり得ますが、通常は正方行列を考えます。
★ 零行列の記号は、O(アルファベットの「オー」)で表す事が多いです。
例えば3次の零行列は、次の通りです。
$$例:3次の零行列 O=\left(\begin{array}{ccc}
0 & 0 & 0\\
0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right) $$
零行列については、行列の演算の方法さえ知っていればすぐに分かるかとは思いますが、
A+O=A、A-O=A、A×O=O×A=Oが成立します。
少し気を付ける必要があるのは、行列の場合は仮に2つの行列の掛け算の結果が零行列だったとしても、もとの行列のいずれも零行列だとは限らないという事です。
$$AB=O\hspace{5pt}であったとしても、\hspace{5pt}A\neq O\hspace{2pt}かつ\hspace{2pt}B\neq O\hspace{5pt}の場合がある$$
簡単な例として2次の正方行列で、零行列でない2つの行列の掛け算が零行列になる場合を挙げておきます。
$$ \left(\begin{array}{cc}
1& 0 \\
0& 0 \end{array}\right) \left(\begin{array}{cc}
0& 0 \\
0 & 1 \end{array}\right)= \left(\begin{array}{cc}
1\cdot 0+0 \cdot 0& 1 \cdot 0+0 \cdot 1 \\
0 \cdot 0+0 \cdot 0 & 0 \cdot 0+0 \cdot 1 \end{array}\right)=O $$
通常の実数などであれば、ab = 0 ⇒ a = 0 または b = 0 が成立します。
行列の場合にはこの関係が成立しないという事です。
対角行列
単位行列のように対角成分以外の成分は全て0で、対角成分に何らかの数(全て1とか全て0の場合を除く)があるものを対角行列と言います。
これは、具体的には様々なものがあり、総称として対角行列と呼びます。
$$3次の対角行列の例: \left(\begin{array}{ccc}
2 & 0 & 0\\
0 & -1 & 0 \\ 0 & 0 & 4\end{array}\right) $$
この形の行列は、もちろん通常の行列よりも計算が簡単になります。
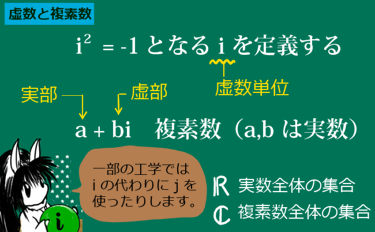
参考:虚数単位の行列表現
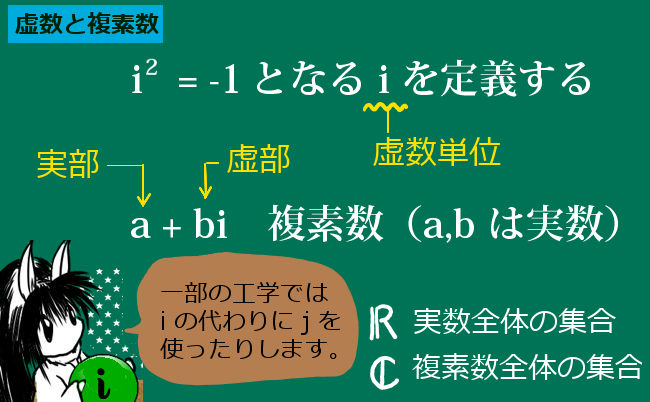
それほど重要ではないので参考程度に述べますが、虚数単位 i に相当する行列も存在します。これを、虚数単位の行列表現と呼ぶ事があります。どういうものかというと、2乗すると単位行列の「-1」倍になる行列という意味です。
$$虚数単位の行列表現:A×A=A^2=-1 を満たすA$$
具体的にはどういうものかというと、2次の正方行列では次のようなものです。
$$A= \left(\begin{array}{cc}
0& 1 \\
-1 & 0 \end{array}\right) $$
試しに2乗を計算してみると、次のようになります。
$$ \left(\begin{array}{cc}
0& 1 \\
-1 & 0 \end{array}\right) \left(\begin{array}{cc}
0& 1 \\
-1 & 0 \end{array}\right) = \left(\begin{array}{cc}
0\cdot 0+ 1\cdot -1 & 0\cdot 1+ 1\cdot 0 \\
-1\cdot 0+ 0\cdot -1 & -1\cdot 1+ 0\cdot 0 \end{array}\right) = \left(\begin{array}{cc}
-1&0 \\
0 & -1 \end{array}\right) =- I $$
関連する事項としては「回転行列」というものがあります。2次の正方行列の要素に三角関数を上手に配置するとうまい具合に加法定理の形になり、「回転」を表せる事に関係します。複素数を極形式で表すと虚数単位 i は複素平面上で「90°回転」を表せるわけですが、その対応として上記の虚数単位に対応する2次の正方行列も回転行列としては90°回転を表すものです。
$$回転行列: \left(\begin{array}{cc}
\cos \theta&\sin \theta \\
-\sin \theta & \cos \theta \end{array}\right) $$
この回転行列で角度部分が90°の時を考えて2乗すれば加法定理によりうまい具合に180°になり、行列としては – I になります。
転置行列・対称行列
続いて、色々な種類の行列を見ていきましょう。
分かりにくい時には具体的な数値を入れてみた行列を考えるとよいと思います。

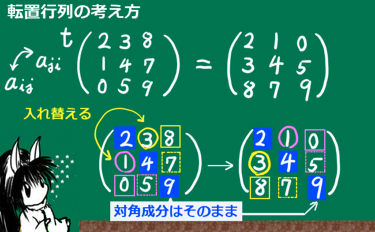
転置行列
ある正方行列の(m,n)成分と、(n, m)成分を全て入れ替えた行列を転置行列(transposed matrix)と言います。ある行列と、その行列の対角成分は全て同じです。
★記号は、行列の左肩にtの文字を書いて表される事が多いです。
3次の場合の例を記すと、次のようになります。
$$A=\left (\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right),\hspace{10pt} ^tA = \left(\begin{array}{ccc}
a_{11} & a_{21} & a_{31}\\
a _{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33}\end{array}\right) $$
$$B=\left(\begin{array}{ccc}
1 & 0& 3\\
2& 4 & -1\\ -2 & 0 & 1\end{array}\right) ,\hspace{10pt} ^tB = \left(\begin{array}{ccc}
1 & 2 & -2\\
0 & 4 & 0 \\ 3 & -1 & 1\end{array}\right) $$
この転置行列は行列の理論の中の計算上、よく出てくるので名称と記号を設定してあります。
転置行列に関して、少し間違えやすくてしかも重要な公式として、掛け算の形の行列の転置行列を考えた時に次の公式が成立します。
$$^t(AB)=(^tB)(^tA)$$
ABはA×Bの事です。
行列の積の転置を考えるときには個々の行列の転置行列を掛け算すればよいという事ですが、掛け算する順番がひっくり返る事に注意が必要です。
対称行列
ある正方行列の(m,n)成分と(n, m)成分が同じである行列を対称行列と言います。
例えば次の形の行列です。
$$\left(\begin{array}{ccc}
a_{11} & a & b\\
a & a_{22} & c \\ b & c & a_{33}\end{array}\right)$$
この形の行列も対角行列などと同じく計算が簡単になるので、理論で好んで使われます。
対称行列は、転置行列がもとの行列に等しいものとしても表せます。
$$対称行列の別の表し方:^tA=A を満たす行列$$
交代行列と直交行列
交代行列とは、転置行列がもとの行列の-1倍になる行列です。この行列も、そのような性質を満たす色々な行列の総称ですが、対角成分は全て0になるという特徴があります。
$$交代行列の定義:^tA=-Aを満たす行列$$
同じく転置行列を使って定義される行列として、直交行列があります。これは、もとの行列と転置行列を掛け算すると単位行列になるというものです。これに関しては、掛け算の順序を入れ替えても同じく単位行列になるという条件がつきます。
$$直交行列の定義:(^tA)A=A(^tA)=Iを満たす行列$$
複素行列
行列の成分として複素数も許容するものを複素行列と言い、なおかつ正方行列の場合は複素正方行列などと呼ばれたりします。
これは、高校の範囲では問題として問われたとしても単なる計算問題なのでさほど重要でないと思いますが、物理の量子力学では行列と複素数の両方を考える都合上、このタイプの行列を一応理論上扱う事になります。そのため、物理を学ぶのであれば後々のために知っておいたほうがよいものです。
いくつか重要な用語としての行列の名称を挙げておきます。
■ 複素共役行列 ■ 随伴行列 ■ エルミート行列・ユニタリ行列・正規行列
複素共役行列
ある複素行列に対して、成分を全て共役複素数にしたものを複素共役行列と呼びます。
記号は、通常の複素数の共役と同様に、文字の上にバーを添えます。
$$A= \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) \hspace{10pt}\overline{A}= \left(\begin{array}{ccc}
\overline {a_{11}} & \overline {a_{12}} & \overline {a_{13}}\\
\overline {a _{21}} & \overline {a_{22}} & \overline {a_{23}} \\ \overline {a_{31}} & \overline {a_{32}} & \overline {a_{33}}\end{array}\right) $$
手でノートに書くといちいち面倒ですが、意味は難しくないと思います。
随伴行列
複素正方行列に対して、共役と転置を両方考えたものを随伴行列と言います。これは、全て要素を共役にして、(m,n)成分を(n,m)成分と入れ替えるという事です。
随伴行列を表す記号は、行列の右肩にアスタリスク*を添えて表す事が多いです。
$$複素正方行列Aの随伴行列:A^*=^t(\overline{A})$$
エルミート行列・ユニタリ行列・正規行列
随伴行列を使って、いくつかの行列の名称が定義されます。
$$エルミート行列: A^*= Aを満たす行列$$
$$歪エルミート行列: A^*= -Aを満たす行列$$
$$ユニタリ行列: A \hspace{3pt}A ^* = A ^* \hspace{2pt} A= Iを満たす行列$$
$$正規行列: A \hspace{3pt}A ^* = A ^* \hspace{2pt} A を満たす行列$$
定義から、ユニタリ行列は全て正規行列です。
エルミート行列は、エルミット行列などと書かれる事もあり、日本語表記だと多少幅があります。
これらの行列の名称は、量子力学などで使う事があります。
逆行列と可逆行列
正方行列Aに掛け算すると単位行列になる行列を逆行列と言います。この逆行列は、必ず存在するわけではなく、存在しない場合もあります。この逆行列が存在する行列を可逆行列と言います。
記号は、行列を「-1乗」した形として表します。ただし、「割り算」とは言わいません。あくまで、行列の積の逆演算という意味合いです。
$$正方行列A の逆行列A^{-1}:AA^{-1}=A^{-1}A=Iをみたす$$
この他に、1つの正方行列に対して決まる数値(実数や複素数)で重要なものもあります。
例えば、次の3つは数学の理論上も、物理等への応用でも重要になります。
- 行列式(デターミナント、determinant):行列式が0でなければ正方行列は可逆行列になる
(※一般のn次の正方行列の行列式の定義は少し面倒) - 跡(トレース、trace):正方行列の対角成分を全て合計した値。行列を群としてみなした場合の理論で使ったりする。応用だと量子化学の理論で使う事もある。
- 固有値:正方行列Aと、列の数が1だけの行列 x(列ベクトルと言います)を使って、Ax = cx を満たす値(実数、複素数)c が存在する時、この c を A の固有値と言う。量子力学でこのタイプの関係式を扱う事があります。