幾何級数（等比級数）

等比数列の和を無限個で考えたものを、「等比級数」または「幾何級数」と言います。
【有限の項数の和のものを同じ名称で呼ぶ事もありますが、ここでは無限級数の場合を扱います。】

収束・発散の条件と計算の仕方

等比数列の和を考え、項数を無限大にしたものはどのようになるかをまとめると次のようになります。

この「等比数列の和のｎ→無限大の極限をとったもの」を「等比級数」と言い、
「幾何級数（geometric series）」という呼び方をする時もあります。
【高校ではこの幾何級数という呼び名はあまり使わないのですが、物理などでは使用する場合もあります。】

具体的に、ａ_ｎ＝(１／２)^ｎ－１で表されるような等比数列の和はｎ→∞の時に収束し、
ｂ_ｎ＝３^ｎで表される等比数列の和はｎ→∞の時に無限大に発散します。

$$\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^{n-1}=\frac{1}{1-\large{\frac{1}{2}}}=2$$

$$\sum_{n=1}^{\infty}3^n=+\infty$$

この時に指数の部分がｎ－１ではなくｎで表されている場合には注意が必要で、例えばｃ_ｎ＝(１／３)^ｎなどと表されている時には計算にｎ＝１の時の「初項」が必要ですので、ｃ_ｎ＝(１／３)・(１／３)^ｎ－１のように考える必要があります。（あるいは、初項ｃ_１＝１／３である事をきちんと把握して計算します。）

$$\sum_{n=1}^{\infty}\left(\frac{1}{3}\right)^{n}=\frac{\large{\frac{1}{3}}}{1-\large{\frac{1}{3}}}=\frac{1}{3-1}=\frac{1}{2}$$

公比が負の数である場合にも、公比の絶対値が１未満であれば同じ公式を使えます。
例えば公比が－１／２などの場合にも和を無限大にとったものは収束します。各項はプラスとマイナスが次々と入れ替わりますが、全体の和は一定値に近づいていくという事です。この場合、上記公式の公比の部分にマイナス符号の公比をそのまま代入します。

$$\sum_{n=1}^{\infty}\left(-\frac{1}{2}\right)^{n-1}=\frac{1}{1+\large{\frac{1}{2}}}=\frac{1}{\large{\frac{3}{2}}}=\frac{2}{3}$$

ところで、これらの無限級数を「幾何級数」とも呼ぶと上述しましたが、「幾何」に何か関係あるのかという話になります。一応、式に平面幾何的な意味を持たせる事は可能です。

適当な図形・・例えば長方形を考えた時に、図形の面積の１／２倍、そのさらに１／２倍、
そしてそのさらに１／２倍、・・の図形を加えていくと、全体の面積は無限には大きくならずに一定の範囲内で収まる事を確認できます。

ａ_ｎ＝(１／２)^ｎ－１の各項はａ_１＝１，ａ_２＝１／２，ａ_３＝１／４，ａ_４＝１／８，ａ_５＝１／１６，・・
のようになりますが、これらの項の和は平面図形で言うと、１つの長方形などの面積に対しておおもとの面積の１倍、１／２倍、１／４倍、１／８倍、１／１６倍、・・を加え合わせていく事に対応します。
この時、項数を増やしても全体の面積は必ず「２未満」におさまり、無限個に増やした場合は収束値である「２」に限りなく近づく事になります。

他方、ａ’_ｎ＝(１／２)^ｎに対する幾何級数を考えた時は収束値は１になる事は上述しましたが、これは平面図形ではａ_ｎ＝(１／２)^ｎ－１に対する幾何級数の収束値２から１を引いた場合に等しく、平面図形では図形の面積の１倍を除いた部分に相当します。

無限小数の級数としての扱い

循環小数を和で表すと？

１÷９＝０.１１１１１１１１１・・・や、１÷３＝０.３３３３３３３３・・・などの
無限循環小数は、幾何級数により表す事ができます。

０.１とは１／１０の事であり、０.０１とは１／１００の事、
そして０.１１とは０.１＋０.０１である事を考えると分かりやすいと思います。

無限循環小数には、０.１２３１２３１２３１２３・・・のように、「１２３」のような複数の番号の組み合わせが繰り返されるものも含まれるわけですが、このようなものも同様に考える事ができます。

０.１２３１２３１２３＝０.１２３＋０.１２３×０.００１＋０.１２３×(０.００１)^ｎ
のようになるので、この場合は公比を０.００１と考えればよいわけです。このようにして、小数が循環する限りは、無限小数は幾何級数とみなす事が可能です。

無理数のように循環しない無限小数は、小数点ごとに項を分けて無限級数で表す事は可能ですが幾何級数として表す事はできません。

0.999999・・・は、「１に等しい」？

「無限級数展開」が意外と身近にある例として、ちょっとしたクイズを考えてみます。

クイズ：「無限小数０.９９９９９９９９・・・・は『１に等しい』ですか？」

もしかすると、意見が割れるかも・・しれませんね。結論を先に言いますと、答えは「１に等しい」、です。

・・すると、「いや、１ではないやろ！？？？」と、怒られるかもしれません。
では、同じ質問を、表現だけ変えてみます：

$$「無限級数 0.9+0.09+0.009+0.0009+・・・=\sum_{n=1}^{\infty}\left\{(0.9)\cdot\left(\frac{1}{10}\right)^{n-1}\right\}は『１に等しい』ですか」 $$

これだと、幾何級数ですね。
これは、明確に答えは「１」なのです。

どういう事かというと、「１に『収束する』」「『極限値と』して１に等しい」という意味において等しくなるという事です。０.９９９９９９９９・・・は、１に限りなく近づくという意味です。

０.９９９９９９９９・・・が１に等しいか・等しくないかで意見が割れてしまうのは、小学校でも教わる無限小数が数学的にはどのような意味を持つかが曖昧な形で教えられている事によります。
前述のように無限小数は正確には無限級数であり、無限循環小数であれば公比の絶対値が１未満の幾何級数になるので１つの値に収束する事になります。

ところで、では例えば１／３＝１÷３＝０.３３３３３３・・・・について、この左辺の分数・割り算の形は本当に幾何級数の公式を使って出てくるでしょうか？試してみると次のようになります。

$$\sum_{n=1}^{\infty}\left\{(0.3)\cdot\left(\frac{1}{10}\right)^{n-1}\right\}=\frac{0.3}{1-\large{\frac{1}{10}}}=\frac{3}{10-1}=\frac{3}{9}=\frac{1}{3}$$

このように、無事に１／３（＝１÷３）に収束する結果となります。

１÷９＝０.１１１１１１１・・・についてもやってみると次のようになります。

$$\sum_{n=1}^{\infty}\left\{(0.1)\cdot\left(\frac{1}{10}\right)^{n-1}\right\}=\frac{0.1}{1-\large{\frac{1}{10}}}=\frac{1}{10-1}=\frac{1}{9}$$

無限級数展開としての位置付け

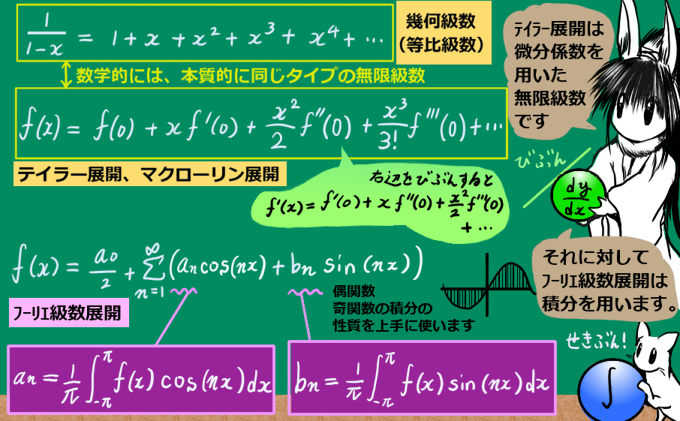
幾何級数は、数学的には１／(ｘ－１)という関数のマクローリン展開と、本質的に同じ無限級数です。
（|x|＜１の範囲でのみ収束するという点まで、本質的に同じです。）

|x|＜１の公比、初項が１の幾何級数を考えると、

$$\lim_{n\to\infty}(1+x+x^2+x^3+\cdots+x^n)=\frac{1}{1-x}$$

これを逆手にとるというか、逆に１／(１－ｘ)という関数を|x|＜１の範囲に限定するという条件付きで無限級数として表すのが、「幾何級数展開」です。本質的には幾何級数の計算と全く同じもので、使い方による名称の違いです。

$$\frac{1}{1-x}=\lim_{n\to\infty}(1+x+x^2+x^3+\cdots+x^n)$$

$$無限大まで和をとる事を前提に、\frac{1}{1-x}=1+x+x^2+x^3+\cdotsと書く事も多いです。$$

これは無限級数展開の中では非常に簡単に理解できるものの１つです。にもかかわらず、大学範囲の数学や物理でも要所で使用します。知っておくと、学習がスムーズになり便利です。

幾何級数展開は、数学の複素関数論で用いられたり、物理では黒体放射の理論で「エネルギーが離散的な値をとること」（つまり量子的である事）の根拠のひとつとして用いられたりもします。他にも、使われ方は色々あります。割と重要なところで突然出てくるのが特徴かもしれません。

ただしそれらは教科書等の中では「幾何級数」「等比級数」である事の説明なしに、唐突に「１／(１－ｘ)＝１＋ｘ＋ｘ^２＋ｘ^３＋ｘ^４＋・・・と『展開』すると・・」などと書かれる事が結構多くあるので、その点だけ注意しましょう。