虚数単位と複素数というものについての定義と基本計算を説明します。
複素数は、微分方程式の解法に使う事ができ、また平面図形的に捉える事も可能である事から物理学の一般の力学や流体力学、電磁気学、電気回路論などで使用される事があります。また、量子力学の波動関数(あるいは「状態」)は、本質的に複素数の関数(実関数も含めて)であると考えられています。

定義と基本用語
まず数学的な定義です。
「2乗してマイナス1になる数」を定義してみるところから始めます。
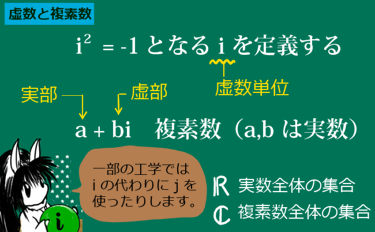
$$i^2=-1$$を満たす「数」を虚数単位(imaginary unit)と言い、
実数 a,b を使って
実数と虚数単位が掛け算や足し算で結びついたような量を考えて、
$$a+bi$$で表される数を複素数)(complex number)と呼びます。
※虚数単位iに対して、定数倍する時には3i,7i といった順番で書く事が多く、
文字式がある場合には同じくbiと書く方法と、意図的にibと書く場合の両方があります。
ibと書いてもbiと書いても、意味はどちらも同じです。
三角関数が虚部にある場合には「i sinΘ」のような順番で書くことが普通です。
◆実数の計算では、
プラス×プラスはプラス、
プラス×マイナスおよびマイナス×プラスはマイナス、
マイナス×マイナスはプラスですので、
これらをどう組み合わせても「2乗してマイナスになる」という場合があり得ないわけです。
複素数を表す文字は何でもいいのですが、z, u , w などが優先して使われる傾向があります。
「複素数 z = a + bi を考えるとき・・・」という具合に使うわけです。
(区別のために実数はa,b,c,・・・で表し、複素数はアルファベットの終わりのz付近のものを使うという単純な理由だと思います。)
複素数の実数だけの部分を実部と言い、虚数単位 i が掛け算されている部分を虚部と呼びます。
複素数zに対して、その実部を Re z と書き、
虚部の虚数単位に掛けられている実数を Im z と書く場合があります。
Re とは real , Im とはimaginary の略です。
$$例えば、z=2+3iに対して \mathrm{Re}\hspace{2pt}z = 2, \mathrm{Im}\hspace{2pt} z = 3 です。$$
また、単に「虚数」と言う場合には、
虚数単位を0以外の実数倍したものだけで構成させるbiという形のものを指す事があり、
これを特に純虚数と呼ぶ事もあります。
これは、複素数a+biにおいてa=0かつb≠0の場合を指しているという見方もできます。
あるいは、「実部が0で、かつ虚部が0でない形で単独で存在する場合を純虚数と呼ぶ事がある」とも言えます。
$$純虚数とは:b\neq 0 として、bi という虚部だけの形で表される複素数$$
虚数、あるいは純虚数という(同じものを指す)呼び方は英名の場合も同じで、
それぞれ imaginary number, purely imaginary number のように言ったりします。
複素数を変数とする関数は複素関数と呼ばれる事があり、その場合の変数となる複素数をzとする時には、そのzを構成する実部と虚部も変数である事からz=x+yiのように書く事もあります。 xとyという2つの実数の変数で決まる関数なので、複素関数は多変数の関数の1つです。
複素数を使う場合には虚数単位を j で表す事があります。
a + bi において b= 0 の時には複素数は通常の実数 a になるので、数学では「実数全体」という集合が「複素数全体」という集合に含まれている、と考えます。
集合の記号で書くとき、
実数全体の集合を \(\mathbb{R}\) 、複素数全体の集合を \(\mathbb{C}\) と書きます。
(これらの記号はそれぞれ、real と complex に由来します。)
複素数全体は実数全体を含みますので、次のような包含関係があります。
$$\mathbb{R}\subset\mathbb{C}$$
◆補足として、
有理数全体の集合 \(\mathbb{Q}\) と整数全体の集合\(\mathbb{Z}\)、自然数全体の集合\(\mathbb{N}\)も含めて包含関係を書くと次のようになります。
$$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$$
共役複素数と複素数の絶対値
複素数 a+bi に対して、 a-bi を共役(「きょうやく」)な複素数、あるいは共役複素数と呼びます。
$$z=a+bi に対する「共役複素数」\bar{z}=a-bi$$ 文字の上に横線を引きます。
この「共役」という用語は、一般的には複素数に限定されたものではなく、
代数学においてより広い意味を持ちます。
また、a+bi に対して、次の量をその複素数の絶対値と言います。
記号では、実数の絶対値記号と同じものを使います。
$$z=a+biの「絶対値」:|z|=|a+bi|=\sqrt{a^2+b^2}$$これは必ず正の実数です。
複素数の絶対値は r などの文字で表す事もあります。
複素数と共役複素数の積は、その複素数の絶対値の2乗に等しくなります。
複素数の絶対値は必ず実数ですから、2つの複素数から実数を確実に作る方法の1つになります。
この性質は結構重要で、式で書くと次のようになります。
$$任意の複素数 z に対して、z\bar{z}=|z|^2$$
この式の証明は、後述する複素数の計算規則を使いますが簡単に行えます。
$$(証明)z=a+biとして、z\bar{z}=(a+bi)(a-bi)=a^2-abi+abi-bi^2=a^2+b^2=|z|^2$$
この簡易的な証明を見ても分かる通り、\(z\bar{z}=|z|^2\) という関係式は、複素数が実数である場合や純虚数である場合にも成立します。
複素数の絶対値の考え方は、複素平面というものを考えるとじつは見やすくて、「実部を底辺、虚部を高さとする直角三角形」の斜辺の長さ、あるいは2点間の距離として捉えらる事ができるのです。
つまり、複素数の絶対値の定義式の「2乗して加えたものの平方根」とは一体何なのかというと、イメージとしては三平方の定理なのです。これは偶然似ているというだけではなくて、割と本質的なものであり理論的にも重要です。
尚、虚部が0の時には複素数は実数になるわけですが、
その時の「複素数の絶対値記号」は実数の絶対値記号としてもきちんと機能するのです。そのために同じ「絶対値」という用語を使い、記号も同じであると考えてもよいでしょう。
複素数の計算方法
2つの複素数 u と w は、
実部同士が等しく、かつ虚部の実数同士が等しい時に限って、
2つの複素数は等しいと呼んで u = w であると書きます。
$$u=a+bi, \hspace{5pt}w=c+di\hspace{5pt}のとき、a=cかつb=dの時、u=w \hspace{5pt} です。$$
★「2つの複素数が等しい」ためにの条件は、じつは定義としなくても計算で「導出」する事が可能です。後述します。
複素数は、実数と同様に加減乗除の計算の中に組み込む事ができて、
式の展開や因数分解などもできます。
複素数の計算をする時には、次の事を踏まえたうえで実数の時と同じように計算します。
- 足し算と引き算の計算では、実部同士だけ、虚部同士だけで必ず行う。
(混ぜ合わせないようにします。) - 掛け算と割り算の計算では、虚数単位 i は実数にくっついた係数であるようにして扱う。
- 計算の際に i の2乗が現れたらそこは -1 に置き換える。 (それによって、計算途中で実部と虚部が入れ替わる事もあります。)
いくつか簡単な計算の具体例を記すと、次のような感じです。
$$加算(足し算):(1+i)+(2+3i)=3+4i$$
$$減算(引き算):(1+i)-(2-3i)=1-2+i(1+3)=-1+4i$$
$$乗算(掛け算):(1+i)(2+3i)=2+3i+2i+3i^2=2+3i+2i-3=-1+5i$$
$$除算(割り算):\frac{2+3i}{1+i}=\frac{(2+3i)(1-i)}{(1+i)(1-i)}=\frac{2-2i+3i-3i^2}{1-i^2}=\frac{2-2i+3i+3}{1+1}=\frac{5+i}{2}$$
4番目の割り算のところはうまく分母と分子に (1-i) を掛けて、分母を実数だけにしています。「複素数と共役複素数の積はその複素数の絶対値の2乗に等しい」という性質を使って、数式上「分母の虚数単位iを消す」という事をしています。この手法は、複素数の微積分を論じる時などにもよく使われます。
ところで、これらの計算を使って、
「2つの複素数が等しいための条件は『実部同士が等しく、かつ虚部同士も等しい』事である」
という命題の「証明」を、次のように行う事ができます。
$$a+bi=c+di$$
であるとすると、
$$a-c=i(d-b)$$
両辺を2乗すると、
$$(a-c)^2=-(d-b)^2\Leftrightarrow(a-c)^2+(d-b)^2=0$$
これを満たすためには a = c かつ b = d という事になります。