慣性の法則とは、古典力学で考えられている運動の3法則の1つです。
一般的には第1番目の前提条件となる法則として挙げられています。
運動の3法則の第1法則
物体に力が働いていない場合、次のいずれかになる:
- 物体は静止し続ける
- 等速『直線』運動をする
この事が成立する座標系が存在する事を「慣性の法則」と呼びます。
慣性とは例えば氷の上を滑るような時は、何か「力」が働いて動いているというよりは惰性で動いていると捉えようという意味です。そして、何かの「力」が働いている事とそうでない事の区別は定量的に「『速度の変化』があるかないか」で考えようというのが力学の理論で、その事は特に運動方程式で表現されています。「速度の変化がない」場合とは物体が止まっている場合も含みますし、滑る場合のように惰性で動いてる場合も両方含んでいます。
慣性の法則は3法則の2番目の運動方程式が成立する「前提条件」となります。
力学では、慣性の法則が成立していなければ運動方程式も成立しないという考え方をします。
運動方程式とは正確にはベクトルを使用した式ですが、
1直線上の運動(1次元の運動)を考える時は次の1式で表されます。$$F=m\frac{d^2x(t)}{dt^2}$$
その前提のもとで、運動方程式からも慣性の法則についての記述を得る事もできます。
※「慣性の法則」自体が運動方程式から証明されるわけではなく、運動方程式によっても慣性の法則の内容が「矛盾なく表現できる」という事であり、理論としての一貫性を持つという事です。
物体が静止または等速運動する事の表現
運動方程式で力がゼロという場合を考えてみましょう。
そうであれば、「加速度もゼロ」という事になります。この時 m は1kgや2kgといった物体の質量で、これは特別な条件を課さない限りは一定値です。
それを踏まえて、微分方程式を所定の計算で解きます。
$$0=m\frac{d^2x(t)}{dt^2}\Leftrightarrow \frac{d^2x(t)}{dt^2}=0\Leftrightarrow \frac{d}{dt}\left(\frac{dx}{dt}\right)=0から、$$
$$\frac{dx}{dt}=C【定数】$$
これは1階微分=0という形の微分方程式で、考え方自体はじつに単純です。一直線上でも物体の速さは、確かに「力が働いていない」時には一定であるという結果になっています。必ずしも速さがゼロ(静止している場合)だけでなく、等速で動いている場合もあり得るという事が数学的な微分方程式の解ともきちんと対応しているので理論としての一貫性を持つという事です。
上記のように定量的な立場で考えてみる時は、氷の上かそうでないかというよりは「速度の変化があるかないか」が重要な要素という事になります。普通の地面や床の上では物を押してもすぐ止まってしまいますが、これも速度の変化と捉えて「摩擦力」を定量的な意味で導入し考察します。
これは物体が接する表面の状態に大きさが依存する力で、氷の場合には摩擦力がごく少ない値でしか発生しないと考えます。
「力が働いていない」という時には、本当に何も力が存在してないと場合と、逆方向に働く力がつり合っている(正確には力ベクトルの補合計がゼロベクトルになる)場合の両方を含みます。もっとも、物理学では何か物体の質量が存在すれば微小であっても力が働くと考えますから、物体の速度が変化しないという場合は厳密にはほとんどの場合後者という事になります。しかしどちらの場合でも、運動方程式上では力が働いていないという事は共通してゼロベクトルで表せます。
直線運動をする事の表現
さて「1階微分=0」という微分方程式として運動方程式を考えた場合、確かに「等速」になるという事の表現はできたわけですが、「軌道の形」についてはまだ何も表していません。
「直線運動」であるかという事については「2階微分=0」のタイプの微分方程式を解く必要があります。

式自体は先ほどと同じです。しかし先ほどは、速さを表すdx/dt=Cという形のままで計算を止めていました。これをさらにx=x(t)で表す事で時間ごとの位置を知る事ができ、物体の「軌跡」を計算できます。
$$0=m\frac{d^2x(t)}{dt^2}\Leftrightarrow \frac{dx}{dt}=Cから、$$
$$x=Ct+B$$
ここでCとBというのは何らかの定数です。この具体的な値を知るには、ある時刻での物体の具体的な位置と速度を知る必要があります(多くの場合t=0の時を考えるのでそれらを「初期値条件」とも言います。)
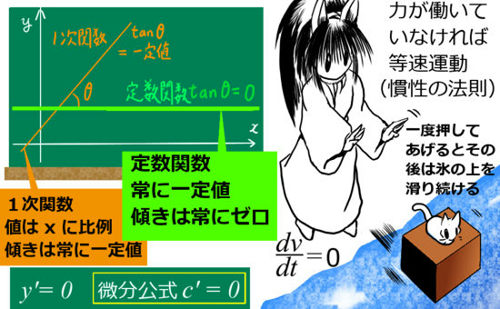
尚、定数関数も何回微分してもゼロになるので解ですが、これは1次関数で C = 0 の場合と見なせるので、定数 C の値に制限を設けなければ定数関数の場合も1次関数に含める事ができます。
1次関数が得られたのでいかにも「直線」っぽいですが、この段階ではそもそも一次元の「直線上」の運動しか考えていないので、これではまだ示した事にはなりません。
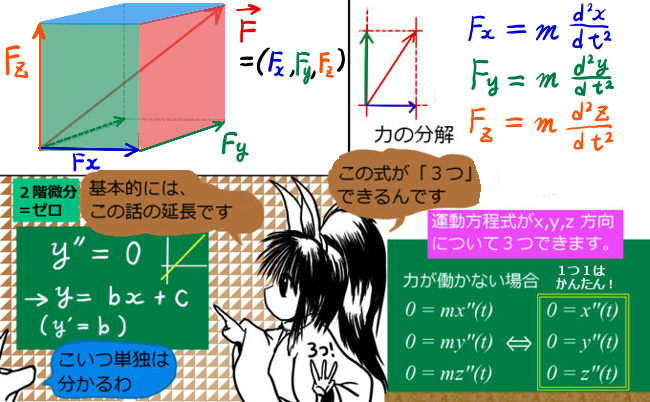
そこでどうするかというと、少なくとも平面上の運動として考えて、微分方程式をx軸方向とy軸方向の2方向について立てる必要があります。空間内の運動なら3方向です。このとき、xやyという直交座標成分は x(t) と y(t)という時間についての関数になります。
$$F_{\Large{x}}=m\frac{d^2x(t)}{dt^2}\hspace{10pt}F_{\Large{y}}=m\frac{d^2y(t)}{dt^2}\hspace{10pt}F_{\Large{z}}=m\frac{d^2z(t)}{dt^2}$$
3つも微分方程式があるといかにも面倒そうですが(実際、一般論としては厄介です)、
ここでは「力が働いていない」場合を考えるだけなので3式とも力の部分に0を入れるだけです。
つまり次のように、3つの「2階微分=0」という式を考えるだけで済みます。
しかもこれら3式は全く同じ形で文字を変えてるだけなのでまとめて解く事ができるわけです。
$$0=m\frac{d^2x(t)}{dt^2}\hspace{10pt}0=m\frac{d^2y(t)}{dt^2}\hspace{10pt}0=m\frac{d^2z(t)}{dt^2}$$
$$ \Leftrightarrow \hspace{10pt} 0=\frac{d^2x(t)}{dt^2}\hspace{10pt}0=\frac{d^2y(t)}{dt^2}\hspace{10pt}0=\frac{d^2z(t)}{dt^2}$$
これらを(まとめて)解く事で、次の3つの通常の連立方程式を得ます。
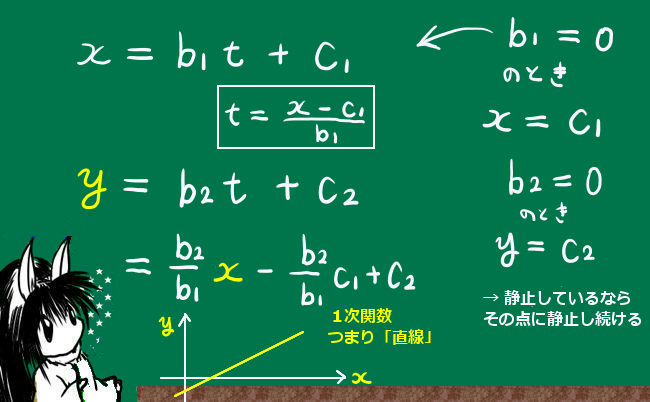
$$x(t) = b_1t+c_1,\hspace{10pt} y(t) = b_2t+c_2 ,\hspace{10pt} z(t) = b_3t+c_3 $$
3式ともtに関する1次式ですから、通常の連立1次方程式と同じく
「tを消去するか、あるいは代入する」方法で、座標成分同士の関係式を作れます。
例えば x と y の関係式は、b1≠0の条件のもとで次のようになります。$$b_2x-b_1y=c_1b_2-c_2b_1\Leftrightarrow y=\frac{b_2}{b_1}x+\frac{c_2b_1-c_1b_2}{b_1}$$
もっとも、あまり具体的な関係式を出す事よりも、ここでは y = Ax + B のような
「1次関数(グラフで言うと直線)」の関係になっているかを見ればじゅうぶんです。
ここではまず、xy平面で物体の軌道は確かに「直線」になる事が示された事になります。
すると全く同じ要領で考えて、
x と z 、y と z の関係も同様にお互いに1次関数の関係にある事が分かります。
また、z = Ax + By + C の形の「3次元での直線」を表す関係式も成立する事も分かります。
(※例えば x + y を考えたうえで t を x, y で表し z の式の t に代入。)
いずれにしても、x, y, z 同士の関係を直交座標(=現実の空間のモデル)上のグラフに描けば直線という事になり、「軌道は直線である」事を意味します。
逆に、もし物体の運動の軌道が曲がっているとすれば、軌道を直線からそらすような何らかの力が働いているという事も意味するという理屈になります。
※物体が「静止」している場合、もちろん軌道は直線にはなりませんが、これは微分方程式の解から考察すると、例えば x 座標成分について x = bt + c で b = 0 の場合、x = c となり、任意の時刻でその位置という事ですから、少なくとも x 軸方向には一切動いていない事を示しています。
y と z についても同様に時間に対して定数であるとすると、結局物体の位置座標は任意の時刻で必ず1点にある=「静止している」という事になります。そのような場合を除くと、物体の位置座標同士の間で必ず1次式の関係を作る事ができ、直線軌道ができるという事です。
つまり、物体に力が働いていなければ物体は静止したままか、「等速」で「直線」運動するという事が運動方程式からも確かに式で表せるという事になります。
運動方程式を「2階」の微分方程式として扱える事から始まり、結論を得る流れを見ましょう。
- 「速度の(1階の)時間微分=加速度」$$\frac{d}{dt}v(t)=a(t)【加速度】$$
- 「位置の(1階の)時間微分=速度」(※位置とはx 座標、y 座標等の事)$$\frac{d}{dt}x(t)=v(t)【速度】$$
- これら2つを合わせると: 「位置の時間による2階微分=加速度」$$\frac{d^2}{dt^2}x(t)=a(t)$$
- 一次元運動の場合、(1直線上の)座標を x(t) とすると
「物体に働く力は、物体の質量と加速度に比例する」という運動方程式は、
$$F=ma(t)\hspace{5pt}\Leftrightarrow \hspace{5pt}F=m\frac{d^2x(t)}{dt^2} と書ける$$ - 平面運動の場合は x(t)、y(t) ごとに、
空間運動の場合、同じく直交座標成分 x(t)、y(t)、z(t) ごとに運動方程式を立てます。
座標成分ごとに3つ作ります。$$F_{\Large{x}}=m\frac{d^2x(t)}{dt^2}\hspace{10pt}F_{\Large{y}}=m\frac{d^2y(t)}{dt^2}\hspace{10pt}F_{\Large{z}}=m\frac{d^2z(t)}{dt^2}$$ - 力が働いていない場合は、力の各成分に0を代入する:
$$0=m\frac{d^2x(t)}{dt^2}\hspace{10pt}0=m\frac{d^2y(t)}{dt^2}\hspace{10pt}0=m\frac{d^2z(t)}{dt^2}$$ 質量mは、両辺で割る事により消去できます。(解に影響を与えないという事です。)
- という事は、「『2階微分=0』という式が3つできる」
→ 時間変数の1次関数が解になる式が3つできる
式で書くなら:\(x(t) = b_1t+c_1,\hspace{10pt} y(t) = b_2t+c_2 ,\hspace{10pt} z(t) = b_3t+c_3\)
t を変数とする1次関数が3つできます - 連立方程式を解く要領で「t を消去」して「x と y」「x と z」「z と x と y」などの関係式を作る。
→すると、x, y, z のそれぞれ同士の関係も「1次関数」になる。
※ y = Ax + B, z = Ax + By + C のような形になります。これらは「直線」の関係です。
(簡単な計算作業で示せます。) - すると結局次の事が癒えます。
→ 「力が働いていない(ゼロ)」という条件のもとで運動方程式を解き、
物体の位置座標(x, y, z)を空間に描くと、その軌道は「直線になる」
→「静止してない物体に力が働かない時、物体は等速の『直線』運動をする」
という慣性の法則の内容がこの段階で、確かに表現される。- 「等速である」事については、加速度を「速度の1階微分」と考えて「1階微分=0」の微分方程式の解から出せます。それを各成分について考えても同じ事で、空間の中の軌道を等速で運動している事になります。
- 等速の「直線運動」とは逆に、軌道が少しでも「曲がっていたら」、それは何らかの力が働いている事も意味します。
力は、多くの場合は物体の速さを変えますが、中には「速さはそのままで『軌道を、直線形からそらす』」というものもあるのです(等速円運動の中心力など)。
このように運動方程式からも「慣性の法則」の内容がきちんと表現できるわけです。
「1階微分=0」「2階微分=0」という微分方程式は数学的にはとても簡単な微分方程式に属するのは間違いありませんが、物理で使う場合に物理的な意味を考えると、考察する事が意外と多くあります。(逆のパターンもあります。物理的に重要ではないけれど、数学的に考察する余地が多くある場合です。)