円周率はなぜ3.14なのか、なぜ「3」ではいけないかの易しい説明です。円や球に対しては「円周率」が常につきまといますが、それについての話をしましょう。
■ そもそも円周率の定義は? ■ 正確な証明の話
そもそも「円周率」の定義は?
円周率とは、「円の直径と円周の長さの比」の事であり、値は約3.14です。
直径が1メートルの車輪の円周の長さは、円周率を用いて
1×3.14=約3.14メートルと計算できます。
円周率の正確な値は3.14159265・・・という、循環しない無限小数であり、「無理数」です。
【無理数である事は、背理法で示します。円周率に限らず、特定の数が無理数である事を示す方法は基本的には背理法です。】
- 「円周の長さ」÷「直径」の値の事を円周率と呼ぶ
- 任意の円において値は一定であり、3.141592・・・・
- 循環しない無限小数であり、無理数である
円周率を使って円の面積も計算できますが、元々は「円周」と直径の比です。
記号は、ギリシャ文字の「パイ」\(\pi\) を使います。
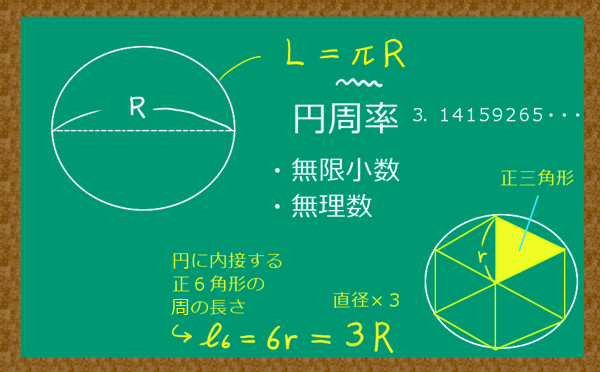
この「約3.14」という半端な数はどこから出てくるのでしょう?
円に内接する正6角形を考えてみてください。
じつは、簡単な計算により、「円の直径×3」は、ちょうど「円に内接する正6角形の周の長さ」なのです。
この事実が、円周率を「約3」と教える事が、数学的に見て決して良いと言えない理由の一つです。
【多角形の円に対する内接・外接の考え方は別途にまとめています。】
★本当に大雑把な計算(例えば100くらいになるのか、1000くらいになるのかといった)であれば円周の長さを「大体3」の計算でやってもよいと思いますが、正確な計算にはならない事は踏まえておく必要があるという事です。実際の値よりも小さくなってしまうからです。
次に、円に内接する正12角形の周の長さを計算してみると、おおよそ、円の直径×3.1058になります。
この「円周率に相当するような定数」は、円に内接する正24角形の場合は約3.1326、
正48角形の場合は約3.1393です。正96角形まで考えると、3.14が出てきます。
じつは、角をもっと増やしていくと、その値は正確な「円周率」の値に限りなく近づくのです。
正確な証明の話
☆ここから先の内容は高校数学、さらに詳しくは大学数学の範囲です。
極限値として円周率が確かに存在する事の証明は少し面倒ですが、平面幾何と極限の基礎知識さえ知っていれば証明は可能です。
円に内接する正n角形と、円に外接する正n角形を考えます。
その中で、2つの頂点と円の中心で作られる三角形に注目します。
ここでじつは少し工夫が必要で、nに対してn+1ではなく、2nを考えます。
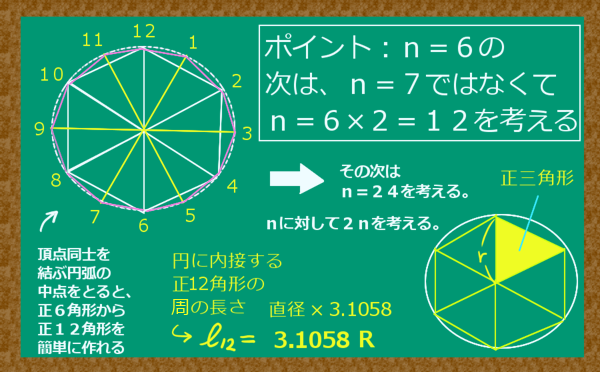
それによって、考察はかなり簡単になるのです。
すると、内接する正2n角形の周の長さは
「内接する正n角形の周の長さより必ず大きい事」と、
「外接する正n角形の周の長さよりは必ず小さい事」が、比較的容易に示せるのです。
これは、内接する正n角形の周の長さを数列として見た時、「単調増加で上に有界」である数列になっている事を示しています。
そして、そのような数列は必ず極限値を持つという定理があるので、
円に内接する正n角形の周の長さは「nを無限大にした時に極限値を持つ」事が示されます。
同様に、円に外接する正n角形の周の長さも極限値を持つ事が示せます。
ここで、証明の中で導出している関係式の一つを用いると、2つの極限値は
一致する事を示せます。その値が、円周率と呼ばれる定数です。
円周の長さが直径と円周率の積で表されるという事実は、三角関数の微分公式が成立する根拠でもあるので、理論上、かなり重要な位置にあると言えます。
★三角関数の微分公式の導出には sin x < x < tan x という不等式を用います。
これは実質的には、「内接正n角形の周の長さ<円周の長さ【極限値】<外接正n角形の周の長さ」という関係式と同等です。
円周や円弧の長さは極限値なので、解析学(微積分学)的には本来は多少詳しい考察や証明が必要になるというわけです。
- 円の接線と内接・外接(図形問題)
- 円と扇形の面積問題(図形問題)
- 正弦定理(図形問題・円と三角形)
- 球の表面積・体積(公式・円と球の関係)
- 円周率の存在証明(証明・図形・極限)
