シグマ記号の使い方（和を表す記号）

和（足し算）を表すのに使うシグマ記号について説明します。

$$英：\sum_{j=1}^n \hspace{10pt}\mathrm{summation\hspace{3pt}notation}$$

記号の意味と使い方

数学で、いくつかの項の和（足し算、合計）を表す時に次の記号を使う事があります。

$$\Large{\Sigma}$$

これはギリシャ文字の「シグマ」の大文字で、英語のアルファベットのＳに相当します。
【ギリシャ語だと実際に「ｓ」の発音らしいです。】
和を表す語（英語だと sum）の頭文字として使っていると言われます。

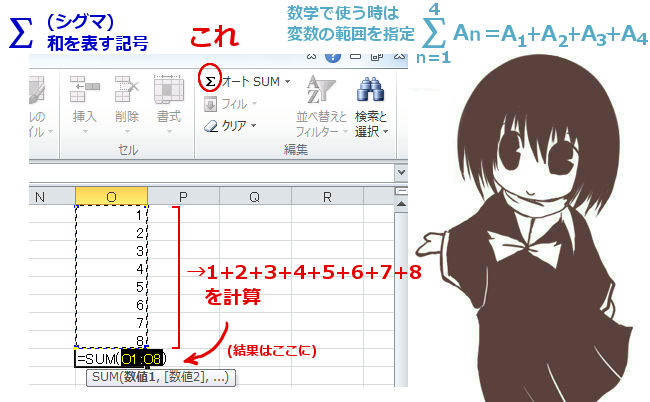
シグマ記号というものは、数学の教科書や本の中でも使われますが、
表計算ソフトの Excel で見た事がある人もいるかもしれません。
使い方はまさしく指定した範囲の数の「合計」の値を計算するというものです。

数学でこの記号を使う時には、もう少しごちゃごちゃと書いてある事が多いです。

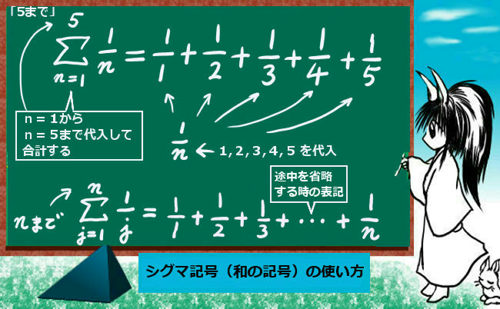
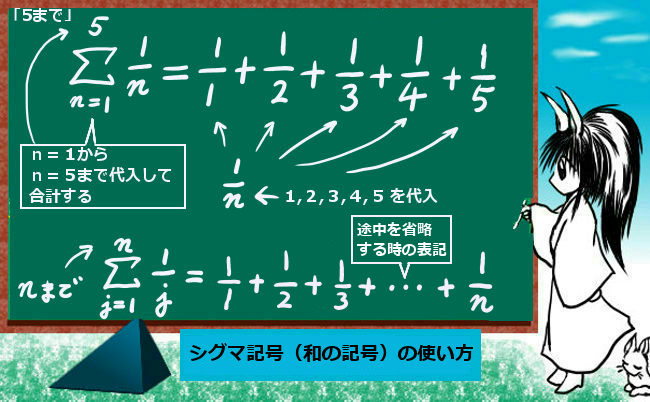
$$\sum_{\large{n=1}}^5\frac{1}{n}$$

これは、記号の次に書かれた１／ｎに「ｎ＝１,２,３,４,５を代入して全部足しますよ」という意味です。
各項の和を具体的に書き下すと次のようになります。

$$\sum_{\large{n=1}}^5\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}$$

変数部分はｎの代わりにｉ、ｊ、ｋなどのてきとうな別の文字を使っても表記できます。
（ｉを使う場合、虚数という事では無くてあくまで変数の番号を表します。）

数列の和を表したり、何かの数のべき乗の和を表したり、様々な和を表すのに使えます。

$$\sum_{\large{i=1}}^7\large{a_i}=\large{a_1+a_2+a_3+ a_4+a_5+a_6+a_7}$$

$$\sum_{\large{j=1}}^7\large{{e^j}}=\large{e+e^2+e^3+ e^4+e^5+e^6+e^7}$$

$$\sum_{\large{m=1}}^5\frac{1}{m^2}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}=1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}$$

「１から始まってｎまで」の和を表す時には、シグマ記号の上のところの番号のところにｎと書きます。

$$\sum_{\large{i=1}}^n\large{A_i}=\large{A_1+A_2+A_3+\cdots +A_{n-2}+A_{n-1}+A_n}$$

$$\sum_{\large{j=1}}^n\large{{e^j}}=\large{e+e^2+e^3+ \cdots +e^{n-2}+e^{n-1}+e^n}$$

略記号的な書き方で、ｎなどのてきとうなところで区切る事を前提としてシグマ記号の上のところを略して書く場合もあります。表記が煩雑なときなどに使われます。どの番号までの和なのか明示したい場合には省略せずに上の番号も書きます。

$$\sum_jF_j(x)\hspace{10pt}\left(\sum_{j=1}^nF_j(x)の略記\right)$$

【※この略記法は一般の教科書などでよく使われますが、試験や入試では使わないほうがいいと思います。】

無限級数を考える場合にはシグマ記号の上のところに無限大の記号（∞）を書きますが、これはより正確に言えばまずてきとうな番号ｎまで和に対して、ｎ→∞の極限を考えたものです。

$$\sum_{\large{n=1}}^{\infty}\frac{1}{n}=\lim_{n\to \infty}\frac{1}{n}=\lim_{n\to \infty}\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots +\frac{1}{1-n}+\frac{1}{n}\right)$$

（なお、この無限級数は収束せず無限大に発散します。）

他に、最初の番号が１ではなくて、別の番号から始める事も表記できます。
その場合は、シグマ記号の下の部分で「ｎ＝１」ではなくて例えば「ｎ＝２」と書けばｎ＝２,３,４,・・について項を加えるという意味になります。

$$\sum_{\large{n=2}}^5\frac{1}{n}=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}$$

$$\sum_{\large{n=3}}^7\frac{1}{n}=\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}$$

普通は番号として自然数（正の整数）を使いますが、０も含めた負の数も含めた整数の範囲にする事もあります。その場合は、例えば－２,－１,０,１,２,・・・を順番に対象の関数などに代入して加えていきます。
（数列の場合は、ａ_ｎといった一般的な形の場合にはｎとして自然数と０を使うのが普通なので、ｎ^２のようなｎ＝・・を直接代入できる形の時に負の整数も代入する表記を使えます。また、１／ｎのように０を代入できないものについては番号として０を含むシグマ記号は使えません。）

$$\sum_{\large{n=0}}^5\frac{1}{n+2}=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}$$

また、高校ではあまり使わないと思いますが、整数を要素とする集合の番号を足し上げるという表記も使われる事があります。例えば、説明のためのごく簡単な例としてＡ＝｛２,３,７,８,１０｝のとき、この番号にわたって和をとる事は次のように書く場合があります。

$$\sum_{\large{n\in A}}^5\frac{1}{n}=\frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{8}+\frac{1}{10}$$

代入する番号は整数であるという前提で、不等式で範囲を指定する表記法も一部あります。

$$\sum_{\large{1≦ i≦ 7}}\large{a_i}=\sum_{\large{ i=1}}^7\large{a_i}=\large{a_1+a_2+a_3+ a_4+a_5+a_6+a_7}$$

変数が複数ある時

やや複雑な例として、変数を２つ含む和を考える事もあります。

$$\sum_{\large{n,m=1}}^3\frac{m}{n}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{2}{1}+\frac{2}{2}+\frac{2}{3}+\frac{3}{1}+\frac{3}{2}+\frac{3}{3}$$

これは、ｎ＝１,２,３とｍ＝１,２,３の「組」にわたって和をとるという意味になります。
つまり、(ｎ,ｍ)＝(１,１), (１,２), (１,３), (２,１), (２,２), (２,３), (３,１), (３,２), (３,３) の９通りについて、
９項の足し算を考えるという時です。

この時に、ｎ＝ｍとなる場合を除いた(ｎ,ｍ)＝(１,２), (１,３), (２,１), (２,３), (３,１), (３,２)の６通りだけの和を考えたいという場合には、シグマ記号の下のところにｎ≠ｍといった表記をして表現する事があります。

$$\sum_{\large{n\neq m\hspace{3pt}n,m=1}}^3\frac{m}{n}=\frac{1}{2}+\frac{1}{3}+\frac{2}{1}+\frac{2}{3}+\frac{3}{1}+\frac{3}{2}$$