タグ: 図形問題

正弦定理は、三角形の辺の長さおよび外接円の半径（あるいは直径）と、三角比の正弦の間に成立する関係式です。（英：sine rule）

三角比を使うという事で高校で教えられる事が多いですが、内容としてはどちらかというと平面の図形問題の色彩が濃く、中学校で教わる平面幾何の内容に近いかもしれません。

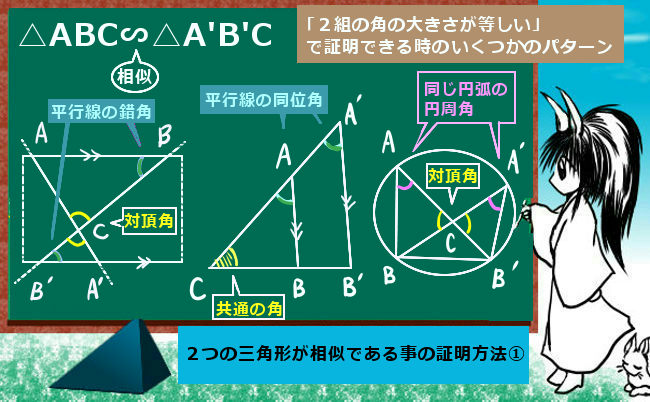
定理の内容

定理の内容は次の通りです。

このように１つの式で表されていますが、２つのグループに分かれていると考える事もできます。１つは辺の長さと正弦の関係、もう１つは辺の長さと正弦と外接円の半径の関係です。（後者については証明を見ると分かるように図形上の意味として肝心なのは「直径」との関係です。）

ここでは２つの部分に分けますが、２つ目のほうを使って最初から全て証明する事も可能です。

証明①：三角形の辺と正弦に関する部分

まず、１つ目の辺の長さと正弦の関係です。
定理の中で言うと、とりあえず外接円の部分は無視した次の部分になります。

$$まずこれを証明します：\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$

２つの等号に関して一度に示す事はできないので、１つずつ証明して最後に全部を結ぶという形になります。

これは、一言で言うと、三角形ＡＢＣの「面積」を３通りの方法で表してみると成立する事が分かる関係式です。本来の「面積」の形の等号関係は次のようになります。

$$\frac{bc\sin A}{2}=\frac{ac\sin B}{2}=\frac{ab\sin C}{2}$$

発想はじつに単純で、三角形の面積「底辺×高さ÷２」において、底辺を辺ＡＢ、ＢＣ、ＡＣのそれぞれとした場合に面積の計算をしてみようという、それだけのものです。

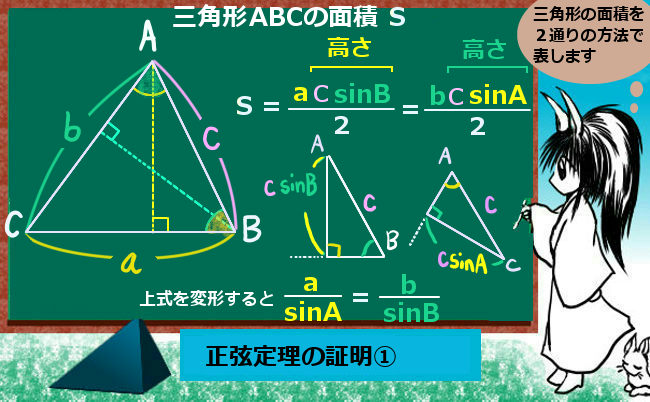
まず。底辺をＡＣ＝ａとした時です。面積を出すには高さが必要ですが、これを三角比の関係を使って表します。ＡＢ＝ｃの斜辺と∠ＡＢＣ＝Ｂの正弦によって、高さはｃsinＢになります。これで、面積の１つが表されるわけです。

$$S=\frac{ac\sin B}{2}$$

底辺をＡＣ＝ｂの部分とみなす場合には、高さがｃsinＡになります。これで面積の２つ目の表し方です。

$$S=\frac{bc\sin A}{2}$$

ここで、いったん２つの式を等号で結びます。
もちろん、同じ面積Ｓを表すので等号で結べます。

$$\frac{ac\sin B}{2}=\frac{bc\sin A}{2}$$

この式で、両辺でｃと１／２は共通しているので掛け算割り算で「消せる」事になり、さらに正弦の部分を両辺で割ると正弦定理の関係式の１つになります。

$$\frac{ac\sin B}{2}=\frac{bc\sin A}{2}\Leftrightarrow a\sin B=b\sin A$$

$$\Leftrightarrow\frac{a}{\sin A}=\frac{b}{\sin B}$$

ここでもう１つ関係式がほしいわけですが、∠ＡＣＢ＝Ｃに関する正弦が足りないので、再びＢＣ＝ａを底辺とする場合に戻って、高さを今度はｂsinＣと考えます。

$$するとS=\frac{ab\sin C}{2}とも表せる事により、\frac{ab\sin C}{2}=\frac{bc\sin A}{2}$$

$$\Leftrightarrow\frac{a}{\sin A}=\frac{c}{\sin C}$$

これで２つの等号関係を結べます。

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}【証明終り】$$

理解の仕方としては、図を見てもっと単純に直観的にという事でもよいと思います。

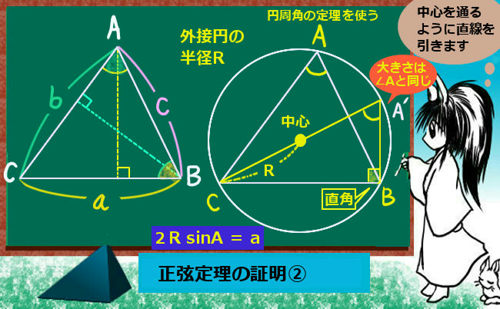
証明②：外接円に関わる部分

次に、正弦定理の内容のうち、外接円の半径を含むほうの部分です。

一体どこから円が関係するのかと思われるかもしれませんが、じつはこの後半部分のほうが、図形的な特徴に気付くと直ちに証明されるので簡単なのです。

この場合には面積を考える必要はなく、三角比の関係だけを使います。

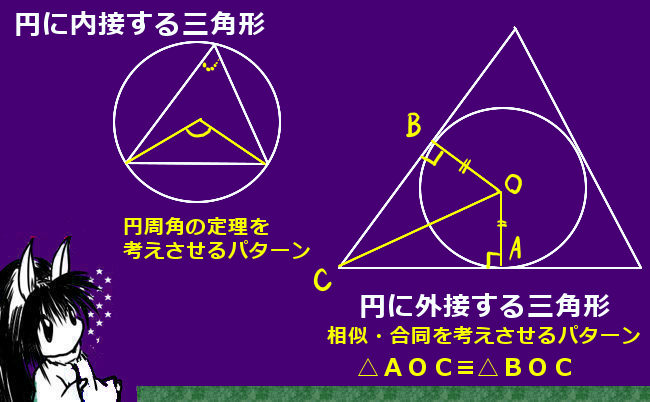
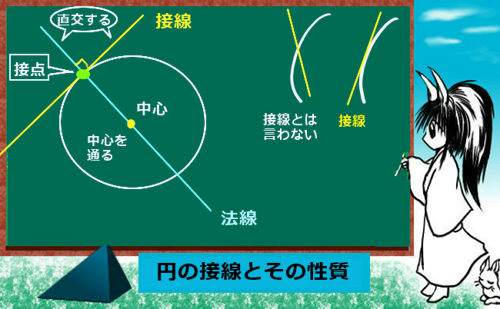
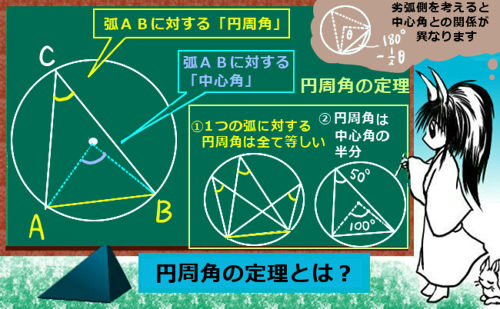
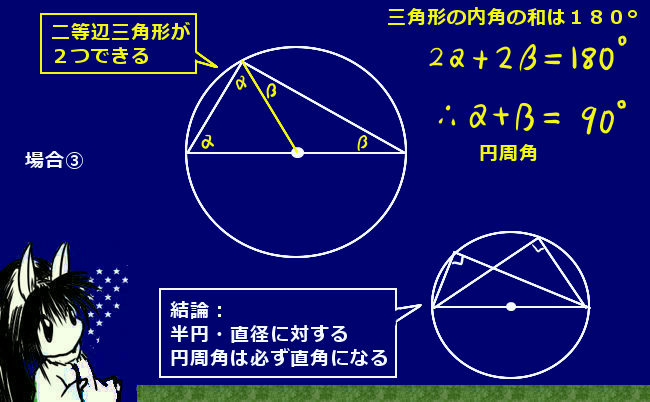
まず外接円を考えるのですが、この時に三角形の１つの頂点から「円の中心を通るように」直線を引きます。それが円周の向かい側とぶつかる点に注目します。

図では、点Ｃから中心に向かって直線を引き、円周との交点をＡ’ としています。

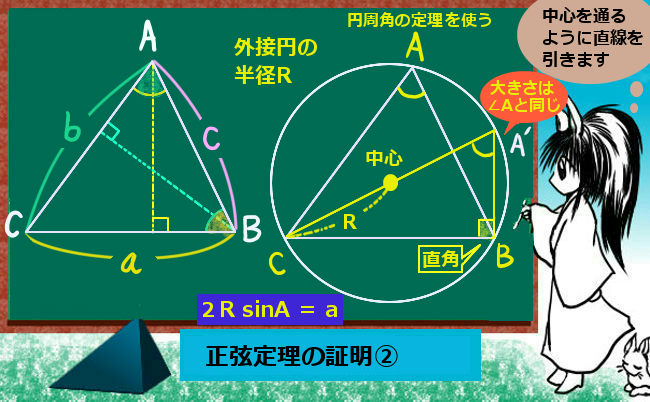
すると、まず円周角の定理により、新しくできた図の∠ＣＡ’Ｂの大きさは∠ＣＡＢ＝Ａと同じ大きさです。（弧ＣＢの円周角なので。）よって∠ＣＡ’Ｂ＝Ａです。

また、図のＣＡ’ は円の直径ですから、その円周角について∠Ａ’ＢＣ＝９０° となります。（これも本質的には円周角の定理によるものです。）

という事は、Ａという大きさの角を含む直角三角形を考える事ができます。斜辺は円の直径（２Ｒ）で、辺ＢＣの長さがａですから両者を三角比の関係で結べます。じつは、これで１つの関係の証明が終りです。

$$三角比の関係により、2R\sin A=a\Leftrightarrow \frac{a}{\sin A}=2R$$

同様にして、頂点Ａや頂点Ｂからも補助線を中心に向かって引く事で残り２つの関係式も得られますが、ａ／(sinＡ)＝ｂ／(sinＢ)＝Ｃ／(sinＣ)を既に証明しているので、これで正弦定理の証明完了としても可です。

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}と合わせて、\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R【証明終り】$$

★こちらのほうの定理の後半の内容について最初に証明する事で前半部分も一度に証明する事もできます。
その場合には頂点と中心を通る補助線を３パターン全て作って、
ａ／(sinＡ)＝２Ｒかつｂ／(sinＢ)＝２ＲかつＣ／(sinＣ)＝２Ｒよりａ／(sinＡ)＝ｂ／(sinＢ)＝Ｃ／(sinＣ)であるとして、定理の前半部分もまとめて証明できます。
手間としては、どちらの方法でもあまり変わらないと思います。

この記事では証明を詳しく記しましたが、理解としてはもっと直感的でよいと思います。

さてこの「正弦定理」、別途に「余弦定理」というものがあるので対として教科書の中で教えられる事も多いのですが、大学入試での出題の可能性を除くと重要度はやや低いものがあるかもしれません。

証明の方法から見ても分かる通り、正弦定理とは本質的には三角形の面積に関する平面幾何の基本事項や、円周角の定理から直結する関係式です。そのためこの定理は直接的というよりは、三角形に関わる多くの事項と間接的に関わっているものと言えるかもしれません。

２つの三角形が合同であるとは、形も大きさも全く同じである事を言います。
形も大きさも同じという事は、面積も等しくなります。

合同な三角形であっても、向きなどが別々の方向を向いていて「見た目」が異なってる場合もあります。２つの三角形が合同であるかを調べるには次の３つの条件を満たしているかを調べます：

合同である三角形は、この３つの条件全てを満たします。つまり、１つの条件を満たせば他の２つの条件も同時に満たされるという事です。合同である事を証明するには１つの条件が満たされている事を示せば十分という事になります。

合同の関係と似ているものとして、相似の関係があります。相似とは「形だけが同じで大きさは違う」というものです。

形も大きさも同じである場合が合同の関係であり、２つの三角形が合同である場合は相似である条件も満たしています。つまり、合同と相似は無関係なものではなくて、形も大きさも等しくなるためのやや厳しい条件が課されるのが合同で、形だけが等しい緩い条件だけが課されているのが相似というわけです。

一見すると合同にはみえないけれどよく見ると合同であるという例は、例えば三平方の定理の証明の１つで見られます。この例では形も大きさも全く同じ三角形が存在するのですが、向いている方向が全く異なるうえに他の様々な線が入り乱れているので気付きにくいのです。

しかし、丁寧に辺の長さや角度を調べると確かに合同である事を示せます。この場合では「２辺とその挟む角が等しい」という条件を使っています。

図の３つの四角形は「正方形」であるという条件があるので、
ＡＣ＝ＡＣ’　ＡＢ＝ＡＢ’　という長さの関係がまずあります。
次に、∠ＢＡＣ＝∠ＣＡＢ＋∠ＣＡＣ’＝∠ＣＡＢ＋９０°ですが、
他方で∠Ｂ’ＡＣ’＝∠ＣＡＢ＋∠Ｂ’ＡＢ＝∠ＣＡＢ＋９０°なので
∠ＢＡＣ＝∠Ｂ’ＡＣ’になります。
ゆえに、△ＡＢＣ≡△ＡＢ’Ｃ’　である、と証明されます。

こういう具合に、合同である事を示すわけです。
尚、この例の場合では、「合同ゆえに面積も等しい」と話が続いていきます。

このように「見ただけでは分かりにくい」場合であっても、辺の長さや角度を調べて合同である事を確かに示せる場合があるわけです。数学的に論証するという事を学ぶ１つの意味がここにあります。単に論理的な思考をするというだけでなくて、事実関係の検証をする１つのツールとしての意味があるという事です。

３辺が全て等しいという条件を使う場合も、たまにあります。例えば、円に外接する三角形の頂点と円の中心で構成される２つの三角形です。

上図において、△ＡＯＣと△ＢＯＣに注目します。
まず、同じ円の半径なのでＯＡ＝ＯＢです。
また、辺ＯＣは共有されているのでもちろん長さは２つの三角形で等しいのです。
さらにここで、∠ＯＡＣ＝∠ＯＢＣ＝９０°なので、三平方の定理によりＡＣ＝ＢＣになります。
よって２つの三角形の３つの辺の長さはそれぞれ等しく、確かに△ＡＯＣ≡△ＢＯＣというわけです。

逆に、見た感じ同じ形・大きさに見えるけれどもきちんと調べるとじつは合同ではないというパターンもあり得ます。描かれた図ではいかにもそれらしく見えるけれども、条件を整理すると合同の３条件のいずれにも当てはまらず「じつは形も大きさも違う」という事が判明する場合もあります。

ここでは、あくまで図形問題に限定してという話ではありますが、「見た目」で判断するのではなく論拠を備えて検証するという事が三角形の合同条件や相似条件の学習において重要なポイントの１つです。これは試験問題を解くという話の中でも重要なので、おさえておきたいところです。

三角形の相似条件は高校入試を始めとして中学数学では重要事項の１つです。

図形問題を解くために必要という事でもありますが、三平方の定理などの重要な定理が成立するための根拠の１つになっている事なども重要と言えるでしょう。

平面において２つの三角形が「相似【そうじ】」であるとは、
ごく簡単に言うと「大きさは違うが形は同じ」であるという事です。

もっとも、単に見た目が似ているというだけでは相似であるとは言わず、きちんと数学的な条件があります。

相似条件と証明での使い方

次の３つの条件の「いずれか」を満たす２つの三角形は互いに相似であると言います。「いずれか」という事は、「１つでも当てはまればよい」という事です。

三角形同士が相似である事がひとたび判明すれば、これら３つの条件は全て成立します。つまり、例えば２組の角度が等しいという条件が成立すれば、３組の辺の長さの比もそれぞれ等しいという事です。

ただし、相似である事を証明するためにはどれか１つだけ判明していればよいという事です。

★比較する２つの三角形が直角三角形であれば、その時点で「対応する１つの角がそれぞれ等しい（９０°で等しい）」事は言えているので、もう１つだけ等しい角度を見つければよいといった作業になります。

繰り返しますが合同条件と似ていますが違うもの（相似条件のほうが制約が緩い）なので注意しましょう。
例えば、辺の長さが分からないけれど角度だけで比較できるのは相似条件のほうであって、合同条件にはそのような条件はないのです。（暗記するのではなく意味を考えてみると分かりやすいと思います。角度だけが分かっている場合、形は同じであっても辺の長さは伸び縮み可能なのです。）

２つの三角形が相似である事を正確に見るには、「証明」が必要です。これは、見た感じ「同じ形」に見えるけれど実際は違う（辺の比が一定にならない、角度が異なる）という事があるからです。

高校入試の出題として多いのは「２組の角の大きさがそれぞれ等しい」事を使うパターンです。これは、同じ大きさの角度である部分が２つ見つかればよいという事です。
より具体的には、対頂角の関係、平行線の同位角・錯角の関係、円周角の定理などを使って「角度の大きさが等しい」事を示します。また、共有する角がある場合にはもちろんその角度は２つの三角形で等しいのです。

残りの２条件は証明の時に使う事もありますが、むしろ相似である事が証明された後に辺の比や面積比を計算させる問いで使われる事が多いように思います。

相似な三角形の面積比

三角形の相似比（辺の長さの比）が１：ｎの場合、面積比は１：ｎ^２になります。
これは、例えば１つの三角についての底辺がｎ倍、高さについてもｎ倍になるためです。

高校入試ではよく問われる事項です。

例えば底辺が２、高さが３の三角形の面積は２×３÷２＝３ですが、
各辺の長さが２倍になったとすると、高さも２倍になる事に注意して
面積は（２×２）×（３×２）÷２＝１２
つまり２×２＝４倍になるという事です。

これは公式として関係式を暗記するのではなく、図に描いてイメージしながら練習してみたほうがよいと思います。

辺の長さの比が１：３ではなく２：３のような場合は面積比は２^２：３^２＝４：９です。

$$辺の長さの比が2:3であれば大きい三角形の面積は小さい三角形の\left(\frac{3}{2}\right)^2=\frac{9}{4}倍$$

辺の比に関する補足説明

相似な三角形の辺の比に関して、補足的な説明をします。

三角形同士が相似である場合に「対応する辺同士の比」は等しくこれを相似比と言うのは前述の通りです。

他方で「同じ三角形の中の辺同士の比」も、相似な２つの三角形で等しくなるのです。これは１つの三角形の中で３通りの比がありますからもちろん一定ではなく、一般的に相似比とも異なる値になります。

しかし、例えば△ＡＢＣでＡＢ：ＢＣ＝１：３であったとすると、それに相似な三角形△ＤＥＦがあったときにＤＥ：ＥＦ＝１：３という事も同じく言えるという意味です。
この時、ＡＣ：ＡＢ＝２：５であれば同様にＤＦ：ＤＥ＝２：５という事です。
（※この場合、この条件だけから具体的な相似比は分からない事には注意。互いの対応する辺の長さの比に関して、相似比という一定の比がある事だけ分かります。）

式で書くと、△ＡＢＣ∽△ＤＥＦであれば、
ＡＢ／ＤＥ＝ＡＣ／ＤＦという比の関係（この一定の比が相似比）に加えて
ＡＢ／ＡＣ＝ＤＥ／ＤＦ　という関係も成り立つという事です。

これは、じつは結構単純な話です。
ＡＢ／ＤＥ＝ＡＣ／ＤＦ　の両辺をＡＣで割り、両辺にＤＥをかける事で得られます。
式変形をしなくても相似関係にあるという事は同じ形で大きさだけが異なると意味を考えれば分かりやすいかと思います。

証明問題も含めて、図形問題が得意になるコツはあまり難しく考えない事です。
意味を考えながら図を描いてみましょう。

他に図形問題として関連が深いのは角の二等分線と三角形の辺の比の関係などで、これは三角形の相似を根拠として成立します。三角形の相似についてじゅうぶん理解していれば、関係式を暗記せずにその場で導出する事も可能なのです。

「形」さえ同じであれば、三角形の中の２辺の「比」が一定であるという事は、三角比の考え方の基礎となっています。これは、直角三角形に限定して、特定の角度に対しては２つの辺の長さは一定になる事を利用して決められるものです。高校数学で教えられるものですが、考え方としては三角形の相似の考え方が分かっていれば理解できる内容になります。

図形問題としての円に対する接線の考え方と、それとセットになる内接・外接の考え方を説明します。

学校で教わる内容としては中学数学・高校入試の範囲ですが、一部はそれ以降の話にもつながる重要事項も含んでいます。なぜかというと微積分での微分係数は関数をグラフ上で図形的に見た場合の「接線」の傾きだからです。また、高校数学では直線を一次関数とみなして種々の考察をして問題を解かせる場合も多いので、円と関わりを持たせた接線の話は中学校以降でも出てくるのです。

円に対する接線の性質

まず「接線」とは何かと言いますと、
「ぴったりくっつくように１点のみで交点を持つ直線」の事を言います。

また、そのよう形で図形同士が交わる時に「接する」という言葉を使います。「直線 L は円Oに接する、接している」といった具合です。（「接線」は必ず直線を指しますが、「接する」という言葉は曲線同士に対しても使います。例えば円と円が「接する」場合というのもあり得ます。）

図形同士が接する点を、「接点」と言います。

同じ１点で交わる場合でも、突き抜けるように交わる直線は接線とは言わないのです。その場合は単純に、１点で交わる交点です。

「接する」という事は数学的に厳密にはどのような条件を要請する事なのか？という事についてはここで触れないで置きますが、図で見れば分かると思います。中学校の範囲では、見て分かるという程度でじゅうぶんです。それで図形問題は解けるからです。

円に対する接線の重要な性質の１つとして、「接点と中心を通る直線は接線と垂直になる」というものがあります。接点を通り接線に垂直な線を法線と言うので「円に対する法線は中心を必ず通る」とも言えます。

どういう理由で１つの接点を通る法線は中心を通るのかというと、図形的には次の通りです。

まず、円周上の２点Ａ、Ｂと円の中心Oからなる三角形は二等辺三角形なので∠AOBが直角になる事はあり得ても、残りの２角は直角にはなり得ません。（三角形の内角の和は１８０°、つまり２直角であるため。）

すると、点Ａに直線が接するには、その直線と線分AOは直角でなければなりません。もし直角でなかったら、その直線上で点Ａ以外にＯまでの距離が等しい点、つまり円周上の点が存在する事になり接線ではなくなってしまいます。

という事は、接線に垂直で接点を通る法線は、接点と中心の両方を通る事になるので題意は示されます。

簡単に言うと、円周上のある点を通る直線は、その点と中心を通る線分に対して垂直である場合に限りその１点のみで交わり、垂直以外の角度の場合には別の円周上の点と必ず交わってしまう（そのような円周上の点が必ず存在する）という事です。

内接と外接

また、図形問題でよく取り上げられますが、円に内接する図形、外接する図形というものがあります。ここで、「外接」の場合は特定の図形が必ず円に「接している」事が要求されますが、「内接」の場合は必ずしも接していなくてもよくて頂点などが全て円を突き抜けない形で触れていれば要請を満たします。

図で見ると分かりやすいでしょう。例えば内接三角形と外接三角形の違いを見てみましょう。

円以外の図形側から見た時、言葉の使い方として内接と外接は逆になります。

つまり、円に内接する三角形側から見れば「円は外接」しています。

三角形に対して円が内接していると言う場合は、円に対しては三角形は外接しているのです。

これらの内接・外接の関係は、図形問題として出題される場合には別の事項と組み合わされる事がほとんどです。例えば、円に内接する三角形・四角形は円周角の定理と組み合わせて問われる事が多いです。円に外接する三角形を考える場合には、中心から接点に向けての線分が接線と直角になる事実を使わせる事が多いです。

ひねったパターンだと、角の二等分線の事項も絡めて三角形の面積比などを問う出題もあります。

複雑にしようと思えばいくらでも問題をひねれるのが内接・外接に関する図形問題の厄介なところですが、必要な定理や数学的事実は限られているという事を押さえる事が重要です。前述した事の中で言えば、「円に対する接線がある時、法線は中心を必ず通る」といった事項です。

そういった、限られた数の基礎事項を確実に押さえたうえで、いろいろなパターンの問題を解いてみる事が中学校でのこの分野を攻略する鍵と言えるでしょう。複雑な定理や人があまり知らないような定理を暗記する必要はないのです。

円周の長さが直径と円周率の積で表されるという事実は、三角関数の微分公式が成立する根拠でもあるので、理論上、かなり重要な位置にあると言えます。

★三角関数の微分公式の導出には sin x ＜ x ＜ tan x という不等式を用います。
これは実質的には、「内接正ｎ角形の周の長さ＜円周の長さ【極限値】＜外接正ｎ角形の周の長さ」という関係式と同等です。
円周や円弧の長さは極限値なので、解析学（微積分学）的には本来は多少詳しい考察や証明が必要になるというわけです。

円周角の定理とは、円の１つの弧に対する円周角の大きさは必ず等しく、しかも中心角の半分の大きさであるというものです。言葉よりも図で見ると分かりやすいでしょう。

この定理は、高校入試（特に公立）では非常に出題頻度が高いものです。しかし逆に高校数学では重要度が減り、大学数学や物理学では基本的には使わないと言ってもよいほどその重要度が下がります。

これは、高校数学以降の話では「円に内接する三角形」よりも「円その物」のほうが対象とする図形として重要である事が大きく関わっていると思います。そのため、円周角の定理とは中学数学というか「円に内接する三角形」という話に限定する範囲においては重要な定理である、という位置付けで理解するとよいかもしれません。

定理の内容と意味

まず、「円周角」とは、円に内接する三角形の１つの角の事で、「その対辺を弦とする円弧のうち長い方（優弧）」に着目して呼ばれるものです。例えば「円弧ＡＢに対する円周角」のように使われます。図で見ましょう。一目で分かると思います。

また、「中心角」とは、ある円弧の弦の両端の点のそれぞれと円の中心を結ぶ線分によって構成される角の事です。これも、図を見ましょう。

円周角の定理の内容は、１つの円弧が固定されている時、その円弧に対する任意の円周角の大きさは等しく、しかもその円弧に対する中心角の大きさの半分であるというものです。

尚、円弧のうち短い方（劣弧）側の弦と結んでできる角も、大きさは互いに必ず等しくなります。ただし中心角との大きさの関係は２：１にはなりません。（中心角の半分を１８０°から引いた大きさになります。）

高校入試を含めて中学数学では、円周角に関する問いは三角形の相似・合同・面積比に関する事項と組み合わされる事が圧倒的に多いです。

また、円周角が直角になる場合とその条件に関しても好まれて出題がなされる傾向があるようです。

「円周角の大きさは必ず中心角の大きさの半分である」という事が定理の主張の１つですが、これを円弧が半円の場合・弦が直径の場合に適用すると円周角は必ず直角であるという事です。

これは、半円の弧の両端を直線で結ぶと必ず円の中心を通るので中心角＝１８０°とみなせる事によります。すると、その円周角はその半分の大きさで９０°つまり直角になるというわけです。後述するように証明する時にはこの事項自体を場合分けで示す必要がありますが、理屈はじつに簡単です。）

証明

円に内接する三角形が内部に中心を含むかそうでないかで場合分けします。

①内接三角形が内部に円の中心を含む場合

円に対する内接三角形が内部に円の中心を含む時、まず最初に分かるのがじつは「円周角は中心角の半分」というほうの事実です。

これは、内接三角形の１つの辺の両端と円の中心で構成される三角形が、必ず二等辺三角形になる事によるのです。

そして、１つの円弧を固定する時、もう１つの円周上の点を動かしても中心角は同じである事に注意します。これは、この条件のもとで１つの円弧に対する任意の円周角は必ず等しい事を意味し、円周角の定理の主張そのものです。

下図で言うと、次のようになります：

$$(180°-2\alpha)+(180°-2\beta)+(180°-2\gamma)=360°\Leftrightarrow 180°-2\alpha=2\beta+2\gamma$$

$$\Leftrightarrow 180°-2\alpha=2(\beta+\gamma)$$

最後の式は「中心角＝円周角の２倍」を表しています。これはこの条件下で点ＡとＢを固定しておけば、点Ｃが移動しても \(\alpha\) の値は変わらないので円周角の定理の内容が成立するのです。

②内接三角形が内部に円の中心を含む場合

次に、内接三角形が内部に円の中心を含まない場合です。この時も、中心角を構成する二等辺三角形をもとにして証明をします。この場合においても二等辺三角形を３つ作ります。

じつは相似関係などを使う必要は特になく、
「三角形の内角の和は１８０°」「四角形の内角の和は３６０°」という、より初歩的な事実関係だけでじゅうぶんなのです。

図で言うと、中心角は \(180°-2\alpha\) で、そこと隣り合う二等辺三角形の中心角に相当する角は \(180°-2\beta\) です。これらを合わせると、\(360°-2\alpha-2\beta\) となります。

しかし、その角度はよく見ると \(180°-2\gamma\) に等しいのです。よって、次の関係が成立しています。

$$180°-2\gamma=360°-2\alpha-2\beta\Leftrightarrow 2(\beta -\gamma)=180°-2\alpha$$

ここで、式に出てくる \(\beta -\gamma\) は何かというと、これはじつは図の円弧ＡＢの円周角です。つまり、この場合でも「中心角＝円周角の２倍」が成立します。

そして、上記２つの場合において点ＡとＢは固定したままでよいという事に注意しましょう。移動するのは、円周角をなす点Ｃだけなのです。中心角は変化しません。という事は、上記２つの場合の円周角は、いずれも中心角の大きさの半分であり、ともに一致するのです。

ゆえに、内接三角形が円の中心を内部に含むかどうかは気にしなくてよい（その事が示された）という事です。

③内接三角形の１辺上に円の中心がある場合

さて、このように場合分けすると、「だったら三角形の１つの辺が『中心を通る場合』も考えなければだめではないか？」という話になります。実際その通りです。

ただし、この第３の場合が、じつは最も簡単なのです。

円周角をつくる頂点から中心に向かって線分を引きます。すると、二等辺三角形が２つできます。ここで、円周角をなす頂点と直径からなる三角形は、２つの二等辺三角形の角だけから構成されるのです。

すると、三角形の内角の和が１８０°である事から、この場合の円周角の大きさは９０°である事が分かるという計算です。

それゆえ、このような場合でも定理の内容は成立しているので、上記２つの場合と合わせてまとめてよいという事になります。

関連事項：円に内接する四角形

同じく中学数学と高校入試で問われる内容として、
「円に内接する四角形の対角線上で向かい合う角の和は１８０°である」というものがあります。

この理由については、円周角の定理を使うとすぐに分かります。

図のように、補助線として対角線を引きます。この時、内接四角形の１つの角が２つの部分から構成されていると考えます。図で言うと ｘとｙで表しています。

$$\alpha=x+yとおきます。$$

それらｘとｙについて、それぞれ異なる円周角であるとみなす事ができるので、それぞれについて定理を適用します。すると、対角線上で向かい合う内接四角形の角の大きさは、１８０°－（ｘ＋ｙ）という事になります。（「三角形の内角の和は１８０°」を使用。）

しかし \(\alpha=x+y\) でしたから、\(\alpha+180°-(x+y)=\alpha+180°-\alpha =180°\) です。これで題意は示された事になります。

円周角の定理は、高校数学での正弦定理を証明するために使われたりもします。