3次元ベクトルに対しては、「外積」と呼ばれるベクトルが定義されます。
「ベクトル積」「クロス積」とも呼ばれます。
◆「微分形式」という数学分野の演算でも「外積代数」という用語を使います。その3次元版では確かに「外積ベクトル」との共通性がありますが、一般には区別されており、微分形式の外積代数で使う記号【∧】による演算を「ウェッジ積」と呼び、
3次元ベクトルに対して外積ベクトルを作る時の記号【×】による演算は「クロス積」もしくは「べクトル積」と呼ぶ事もあります。
(英語の場合、3次元ベクトルの外積ベクトルを指す語としては、「べクトル積」に該当する vector product という表現を使う事が多いです。)
高校では数学でも物理でも外積を直接計算する事はほとんどないと思いますが、力と磁場と電流の向きの関係などで間接的に関わっています。そういった関係を、数学的にもう少し詳しく定式化したものが外積ベクトルになります。
定義と考え方
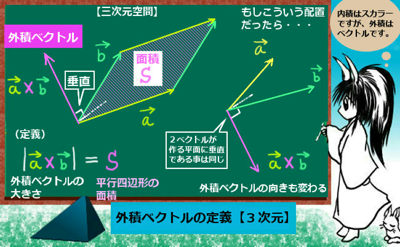
外積ベクトルは、3次元空間内の2つのベクトルから作られる別のもう1つのベクトルの事で、次のような定義のもとで使用します。
3次元の空間ベクトル \(\overrightarrow{a}と\overrightarrow{b}\) とから作られる外積ベクトル(あるいは単に「外積」)は、次のように$$\overrightarrow{a}×\overrightarrow{b}$$と書き、向きと大きさを次のように定義します:
- 大きさ:\(\overrightarrow{a}と\overrightarrow{b}\) が作る平行四辺形の面積に等しいとする
- 向き:\(\overrightarrow{a}と\overrightarrow{b}\) が作る平面に対して垂直
【\(\overrightarrow{a}から\overrightarrow{b}\)に向けてより小さい角度で「右ねじ」を締める時のネジ回しの先端の方向】
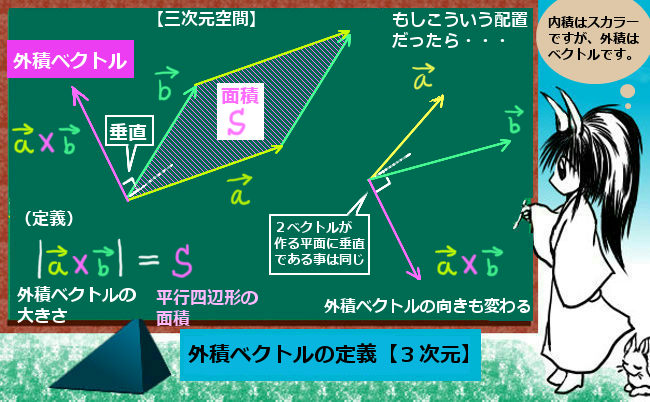
通常のスカラー値やスカラー関数の場合、掛け算の記号はA×B、A・B、ABのいずれでも同じ計算を表すと約束しますが、ベクトルの場合には、「\(\overrightarrow{a}\cdot\overrightarrow{b}\)は必ず内積」「\(\overrightarrow{a}×\overrightarrow{b}\)は必ず外積」を表すものと定義します。
外積ベクトルの大きさに関しては、2つのベクトルが作る平行四辺形の面積ですから、ベクトルの成分さえ分かれば一応計算できる事になります。
外積ベクトルの「向き」については、2ベクトルが作る平面(平行四辺形も含めて)に「垂直」という定義ですが、この時に表側の方向への垂直なのか、裏側の方向への垂直なのか2パターン存在します。
そのどちらかに必ず1つに決めるための基準が「右ネジを回す方向」というわけです。(これは少し直感的な説明の仕方ではあるのですが、物理学でもよくなされます。)
ネジを締める時に、時計回りにネジ回しを回せば締まっていくタイプのネジを考えます。
(反時計回りに回すと締まる「逆ネジ」も存在しますが、それは考えない。)
普通は上から見下ろしてネジを回しますが、仮に天井に向けてネジを回して締める時には「下から見れば時計回り」ですが、「上から見ると反時計回り」に見える事に注意します。
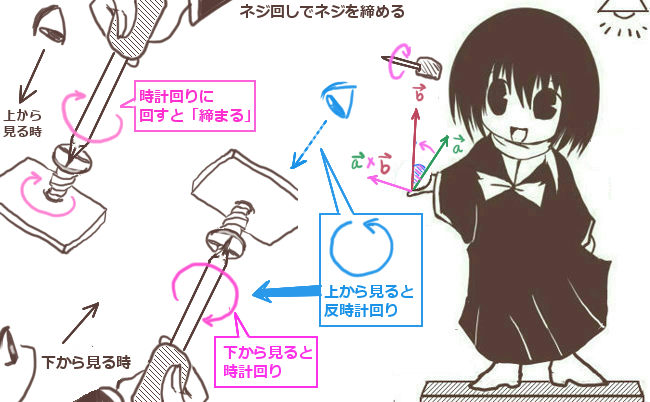
外積ベクトル\(\overrightarrow{a}×\overrightarrow{b}\)の始めに書かれているほう(ここでは\(\overrightarrow{a}\)のほう)から、「時計回りに回せば『より小さい角度で』もう1つのベクトルに辿り着く」視線の方向を考えます。2つベクトルが作る平面の「表」から見るか、「裏」から見るかという事です。z軸のプラスマイナスを基準として上側(プラス方向)から見るか、下側(マイナス方向)から見るかの違いとも言えます。
z軸を基準にした時に上から見た時に、\(\overrightarrow{a}\)から時計回りに(ネジを締める方向に)回して「より小さい角度」で\(\overrightarrow{b}\)に至る状況だったとしましょう。この時は、外積ベクトル\(\overrightarrow{a}×\overrightarrow{b}\)の向きは、斜めになりながらもz軸の上から下に向かう方向に向いています。(実際、外積ベクトルのz成分の符号はマイナスになります。)
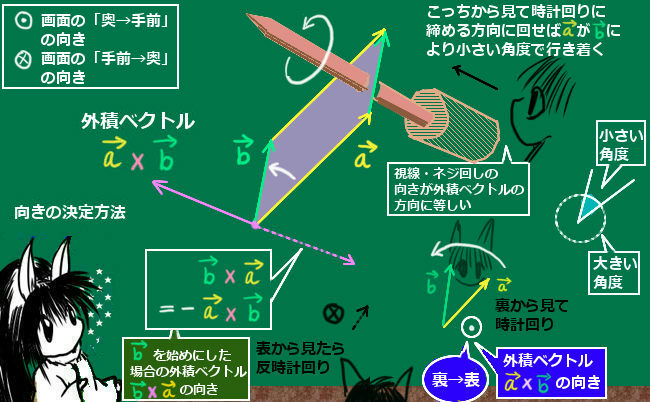
弓矢の「矢」の矢先が眼前に飛んでくるイメージで「丸に点・」の記号で「奥→手前」を表し、
矢の後部についている「羽」が後ろから見えているイメージで「丸にバツ×」の記号で「手前→奥」の向きを表します。
演算と基本公式
外積ベクトルに関しては、幾つかの簡単な公式が成立します。
- \(\overrightarrow{a}×\overrightarrow{a}=0\) 【一応「ゼロベクトル」。平行四辺形が潰れてしまうので】
- 2つのベクトルが平行であれば\(\overrightarrow{a}×\overrightarrow{b}=0\)
- 2つのベクトルが直角であれば \(|\overrightarrow{a}×\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|\) 【平行四辺形が長方形となるためです。】
- k を実数として、\((k\overrightarrow{a})×\overrightarrow{b}=\overrightarrow{a}×(k\overrightarrow{b})=k(\overrightarrow{a}×\overrightarrow{b})\) 【ベクトルの定数倍に対する扱い】
- \(\overrightarrow{a}×(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}×\overrightarrow{b}+\overrightarrow{a}×\overrightarrow{c}\) 【分配則】
- \(\overrightarrow{a}×\overrightarrow{b}=-\overrightarrow{b}×\overrightarrow{a}\) 【交代性。可換でない(交換則が成立しない)事に注意】
これらのうちの交代性と分配則については、もう少し詳しく述べます。
外積ベクトルの交代性
外積ベクトル\(\overrightarrow{a}×\overrightarrow{b}\) に対して、外積を構成するベクトルの配置は全く同じで式の中の順番だけ入れ替えた\(\overrightarrow{b}×\overrightarrow{a}\) という外積を考えると考えるとどうなるでしょうか?
この場合は、下から見て時計回りにネジを締めようとする事で条件を満たすので、向きは\(\overrightarrow{a}×\overrightarrow{b}\)と同一直線にあって「逆向き」になります。
言い換えると、ベクトルの外積は、演算に使う2つのベクトルの順番を変えると符号が逆転します。【内積は2つのベクトルの順序はどちらでもよい事に注意。】
$$\overrightarrow{a}×\overrightarrow{b}=-\overrightarrow{b}×\overrightarrow{a}$$
この時に外積ベクトルの成分も各々符号が反転します。
例えば簡単な例で言うと、\(\overrightarrow{a}×\overrightarrow{b}\)=(1,-2,5)であったとしたら、
\(\overrightarrow{b}×\overrightarrow{a}\)=-\(\overrightarrow{a}×\overrightarrow{b}\)=(-1,2,-5)になるという事です。
外積ベクトルの分配則【証明】
分配則については、一見「当たり前」のようですが、外積ベクトルの定義が多少込み入ったものである事や、可換性については成立していない(代わりに交代性が成立)事から、実はそれほど自明な事ではないとも言えます。
証明は、空間の幾何を考える方法があります。
まず、\(\overrightarrow{b}と\overrightarrow{c}と(\overrightarrow{b}+\overrightarrow{c})\) の3つのベクトルで作られる三角形を考えます。そして、その三角形の各点から\(\overrightarrow{a}\) が伸びているような図を考えます。
次に、\(\overrightarrow{b}の始点から伸びる\overrightarrow{a}\)に対して\(\overrightarrow{b}\) の終点から垂線を引き、その足となる点をHBとします。
同様に、\(\overrightarrow{c}の終点から伸びる\overrightarrow{a}\)に対して\(\overrightarrow{b}\) の終点(\(\overrightarrow{c}\) の始点)から垂線を引き、
その足となる点をHCとします。
また、\(\overrightarrow{b}\) の終点であり\(\overrightarrow{c}\) の始点でもある点をAと置きます。
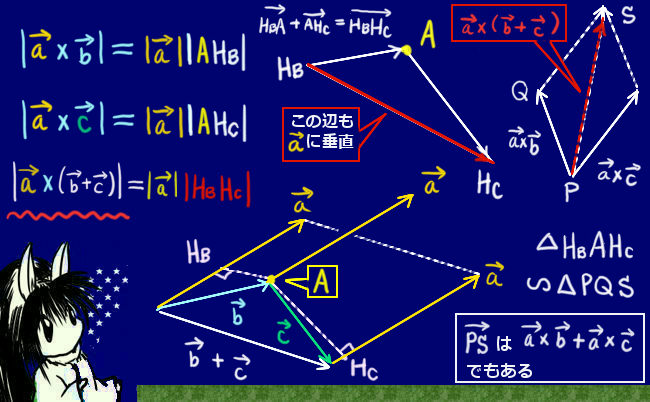
この時、AHB、AHC、HBHCはそれぞれ平行四辺形の高さになっています。
HBHCは\((\overrightarrow{b}+\overrightarrow{c})と\overrightarrow{a}\)が作る平行四辺形の高さです。
(\(\overrightarrow{AH_B}と\overrightarrow{AH_C}がともに\overrightarrow{a}\)に垂直なので辺HBHCも\(\overrightarrow{a}\)に垂直です。内積を考えると少し分かりやすい。)
そこで、3つの外積ベクトルの「大きさ」をそれらの辺の長さで表す事ができます。
(単純に「平行四辺形の面積=底辺×高さ」で計算します。)
- \(|\overrightarrow{a}×\overrightarrow{b}|=|\overrightarrow{a}||AH_B|\)
- \(|\overrightarrow{a}×\overrightarrow{c}|=|\overrightarrow{a}||AH_C|\)
- \(|\overrightarrow{a}×(\overrightarrow{b}+\overrightarrow{c})|=|\overrightarrow{a}||H_BH_C|\)
ここで、これら3つの外積ベクトルがぴったり「三角形」を作れるかが実は自明ではありません。
しかしこの計算結果から、3つの外積ベクトルの大きさの比は、三角形AHBHCの辺の比に全く等しい事になります。つまりそれらは互いに相似な三角形になっている事を意味し、従って3つの外積ベクトルはきちんと「三角形」を形成する事になります。
さらに、\(\overrightarrow{a}×\overrightarrow{b}\)と\(\overrightarrow{a}×\overrightarrow{c}\)の2つのベクトルに対する斜辺は\(\overrightarrow{a}×\overrightarrow{b}+\overrightarrow{a}×\overrightarrow{c}\)と(常に)表せるので、\(\overrightarrow{a}×(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}×\overrightarrow{b}+\overrightarrow{a}×\overrightarrow{c}\) という事になります。【証明終り】
成分表示の方法(外積ベクトルの成分と射影面積の関係)
外積ベクトルはベクトルですので【内積はスカラー】、通常のベクトルと同様にx、y、z座標の成分を持ちます。そして2つの空間ベクトル\(\overrightarrow{a}と\overrightarrow{b}\) の成分が分かっていれば、外積ベクトル\(\overrightarrow{a}×\overrightarrow{b}\)の成分も一意的に決定します。
まず結論は、次のようになります。
$$\overrightarrow{a}=(a_1,a_2,a_3),\hspace{10pt}\overrightarrow{b}=(b_1,b_2,b_3)である時$$
$$\overrightarrow{a}×\overrightarrow{b}=(a_2b_3-b_2a_3,\hspace{5pt}a_3b_1-a_1b_3,\hspace{5pt}a_1b_2-b_1a_2)$$
ここで、
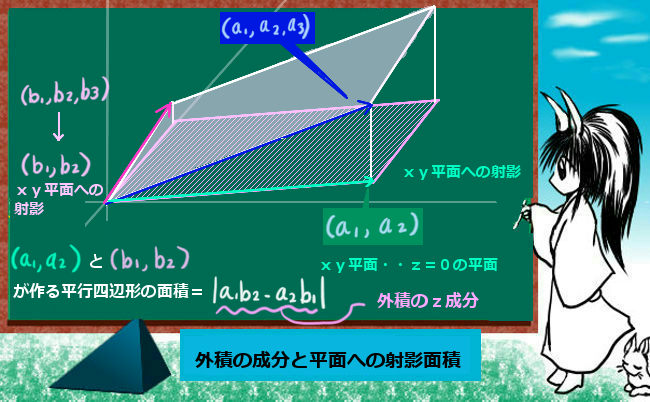
第1成分の絶対値は平行四辺形のyz平面への射影面積、
第2成分の絶対値は平行四辺形のxz平面への射影面積、
第3成分の絶対値は平行四辺形のxy平面への射影面積になります。
(※絶対値が「面積」に必ず等しいという事であり、外積ベクトルの各成分の符号はプラスの場合もマイナスの場合もある事には注意。各成分の符号が外積ベクトルの向きも決定します。)
外積ベクトルの成分と射影面積の関係について、空間上の平行四辺形の各平面への射影もまた「平行四辺形」になっている事は、ベクトルによる平行四辺形の面積公式の形から分かります。
例えば外積ベクトルのz成分 a1b2-a2b1は、xy平面上の平面ベクトルが作る平行四辺形の面積公式の形そのものです。
外積ベクトルの交代制から、外積を構成するベクトルの順序を入れ替えると(ベクトルの配置自体は同じ)、次のような差の順番が入れ替わったような形の成分表示になります。$$\overrightarrow{b}×\overrightarrow{a}=(b_2a_3-a_2b_3,a_1b_3-a_3b_1,a_2b_1-b_2a_1)$$
成分表示についての証明
このように成分表示できる事の証明は、単位ベクトルによるベクトル表記と分配則を使うと意外と簡単に済みます。
$$\overrightarrow{e_1}=(1,0,0),\hspace{5pt}\overrightarrow{e_2}=(0,1,0),\hspace{5pt}\overrightarrow{e_3}=(0,0,1)\hspace{5pt}のもとで$$
$$\overrightarrow{a}=a_1\overrightarrow{e_1}+a_2\overrightarrow{e_2}+a_3\overrightarrow{e_3},\hspace{10pt}\overrightarrow{b}=b_1\overrightarrow{e_1}+b_2\overrightarrow{e_2}+b_3\overrightarrow{e_3}\hspace{10pt}と書けます。$$
このような表された形のもとで外積の公式を使いながら計算して整理すると、外積ベクトルの成分表示が確かに得られます。
使う公式と性質は次の通りです。
- 「分配則」を使って、通常の展開式のように計算していきます。
添え字の順番を変えると外積の符号が変わってしまうので注意。 - 「同じベクトル同士の外積は0」つまり\(\overrightarrow{e_1}×\overrightarrow{e_1}=0\) のようになる事を使うと幾つかの項が0になって消えます。
- 分配則に従って展開した後で、「交代性」\(\overrightarrow{a}×\overrightarrow{b}=-\overrightarrow{b}×\overrightarrow{a}\)も使用して式を整理します。
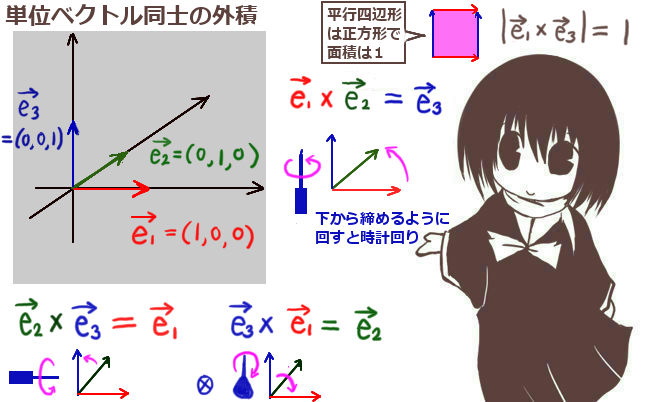
- 異なる単位ベクトル同士は、成す角度が直角であり、作る平行四辺形は正方形であって大きさは1です。さらに単位ベクトル同士の位置関係にも注意して、
\(\overrightarrow{e_1}×\overrightarrow{e_2}=\overrightarrow{e_3}\)
\(\overrightarrow{e_2}×\overrightarrow{e_3}=\overrightarrow{e_1}\)
\(\overrightarrow{e_3}×\overrightarrow{e_1}=\overrightarrow{e_1}\hspace{5pt}\) となる事を最後に使います。
$$\overrightarrow{a}×\overrightarrow{b}=(a_1\overrightarrow{e_1}+a_2\overrightarrow{e_2}+a_3\overrightarrow{e_3})×\overrightarrow{b}=b_1\overrightarrow{e_1}+b_2\overrightarrow{e_2}+b_3\overrightarrow{e_3}$$
$$=a_1b_2(\overrightarrow{e_1}×\overrightarrow{e_2})+a_1b_3(\overrightarrow{e_1}×\overrightarrow{e_3})+a_2b_1(\overrightarrow{e_2}×\overrightarrow{e_1})+a_2b_3(\overrightarrow{e_2}×\overrightarrow{e_3})+a_3b_1(\overrightarrow{e_3}×\overrightarrow{e_1})+a_3b_2(\overrightarrow{e_3}×\overrightarrow{e_2})$$
$$=(a_2b_3-a_3b_2)(\overrightarrow{e_2}×\overrightarrow{e_3})+(a_3b_1-a_1b_3)(\overrightarrow{e_3}×\overrightarrow{e_1})+(a_1b_2-a_2b_1)(\overrightarrow{e_1}×\overrightarrow{e_2})$$
$$=(a_2b_3-a_3b_2)\overrightarrow{e_1}+(a_3b_1-a_1b_3)\overrightarrow{e_2}+(a_1b_2-a_2b_1)\overrightarrow{e_3}$$
$$=
(a_2b_3-b_2a_3,\hspace{5pt}a_3b_1-a_1b_3,\hspace{5pt}a_1b_2-b_1a_2)【証明終り】$$
外積ベクトルの成分表示は、次のように証明する事もできます。
外積ベクトルの成分を(X,Y,Z)とおいて計算してみます。これらの未知数を算出する計算になります。
まず、次のように置いておきます。$$a_2b_3-a_3b_2=S_1,\hspace{5pt}a_3b_1-a_1b_3=S_2,\hspace{5pt}a_1b_2-a_2b_1=S_3$$
外積ベクトルの定義から、構成する2つのベクトルとの直交性(内積の値が0)と、3次元の場合の平行四辺形の面積公式の3式を書きます。
$$①\overrightarrow{a}との直交性:a_1X+a_2Y+a_3Z=0$$
$$②\overrightarrow{b}との直交性:b_1X+b_2Y+b_3Z=0$$
$$③面積【2乗を計算】:X^2+Y^2+Z^2=(a_2b_3-b_2a_3)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2$$
$$\Leftrightarrow X^2+Y^2+Z^2=S_1\hspace{1pt}^2+S_2\hspace{1pt}^2+S_3\hspace{1pt}^2$$
①式に\(b_1\)、②式に\(b_1\) を掛けて2つの式を引き算すると、
\((a_1b_2-a_2b_1)Y=(a_3b_1-a_1b_3)Z \Leftrightarrow S_3Y=S_2Z\) となります。
同じ手順で1つの変数を消去する方法を使うと、
\(S_1Y=S_2X\)および\(S_3X=S_1Z\) となります。
ここで、面積のほうの式③の両辺に\(S_1\hspace{1pt}^2\) を掛けると、次のようになります。
$$S_1\hspace{1pt}^2X^2+S_1\hspace{1pt}^2Y^2+S_1\hspace{1pt}^2Z^2=S_1\hspace{1pt}^2(S_1\hspace{1pt}^2+S_2\hspace{1pt}^2+S_3\hspace{1pt}^2)$$
$$\Leftrightarrow S_1\hspace{1pt}^2X^2+S_2\hspace{1pt}^2X^2+S_3\hspace{1pt}^2X^2=S_1\hspace{1pt}^2(S_1\hspace{1pt}^2+S_2\hspace{1pt}^2+S_3\hspace{1pt}^2)$$
$$\Leftrightarrow (S_1\hspace{1pt}^2+S_2\hspace{1pt}^2+S_3\hspace{1pt}^2)X^2=S_1\hspace{1pt}^2(S_1\hspace{1pt}^2+S_2\hspace{1pt}^2+S_3\hspace{1pt}^2)\Leftrightarrow X^2=S_1\hspace{1pt}^2$$
同様に計算すると、\(Y^2=S_2\hspace{1pt}^2およびZ^2=S_3\hspace{1pt}^2\)となります。
X、Y、Zの値としてそれぞれプラスとマイナスの2つ候補が出てきますが、既に得られているX、Y、Zの関係式と、外積ベクトルの向きの定義に合う組み合わせから、ここでの計算の場合では「全てプラス符号」です。(具体的な値を代入して試してみると分かりやすいです。)
それにより、\(X=S_1=a_2b_3-b_2a_3,\hspace{5pt}Y=S_2=a_3b_1-a_1b_3,\hspace{5pt}Z=S_3=a_1b_2-a_2b_1\) となります。
ベクトル三重積
外積はベクトルなので、
「あるベクトルと、別の外積ベクトルとの『外積』」というのも計算としてはあり得ます。
つまり、\(\overrightarrow{A}\)×(\(\overrightarrow{B}\)×\(\overrightarrow{C}\)) のような計算も可能であるわけです。
このタイプの計算を「ベクトル三重積」と呼ぶ事があります。次の形の計算が可能です。
$$\overrightarrow{A}×(\overrightarrow{B}×\overrightarrow{C})=(\overrightarrow{A}\cdot\overrightarrow{C})\overrightarrow{B}-(\overrightarrow{A}\cdot\overrightarrow{B})\overrightarrow{C}$$ また、外積ベクトルを作る順番を変えると計算結果も変わり、次式になります。 $$(\overrightarrow{A}×\overrightarrow{B})×\overrightarrow{C}=-(\overrightarrow{B}\cdot\overrightarrow{C})\overrightarrow{A}+(\overrightarrow{A}\cdot\overrightarrow{C})\overrightarrow{B}$$
この公式中で、内積はスカラーなので、\((\overrightarrow{A}\cdot\overrightarrow{C})\overrightarrow{B}\) などは例えば\(3\overrightarrow{B}\) のようなベクトルの定数倍のようなものを表します。(スカラー関数倍という場合もあり得ます。)
◆ベクトルの「内積」の場合は、ベクトルとベクトルからスカラーを作る演算なので、3つ以上のベクトルに対する内積の演算は存在しないわけです。
ベクトル三重積の公式を証明するには、外積ベクトルの成分表示を使うと比較的簡単です。(少しの計算は必要ですが。)
まず、\(\overrightarrow{A}\)×(\(\overrightarrow{B}\)×\(\overrightarrow{C}\)) のx成分から計算すると次のようになります。
$$x成分:a_2(b_1c_2-c_1b_2)-a_3(b_3c_1-c_3b_1)=b_1(a_2c_2+a_3c_3)-c_1(a_2b_2+a_3b_3)$$
$$=b_1(a_1c_1+a_2c_2+a_3c_3)-c_1(a_1b_1+a_2b_2+a_3b_3)=(\overrightarrow{A}\cdot\overrightarrow{C})b_1-(\overrightarrow{A}\cdot\overrightarrow{B})c_1$$
途中の計算で、a1b1c1-a1b1c1(=0)を式に加えています。
同様の計算で、y成分とz成分は次のようになります。
$$y成分:(\overrightarrow{A}\cdot\overrightarrow{C})b_2-(\overrightarrow{A}\cdot\overrightarrow{B})c_2\hspace{10pt}z成分:(\overrightarrow{A}\cdot\overrightarrow{C})b_3-(\overrightarrow{A}\cdot\overrightarrow{B})c_3$$
よって、全て合わせると公式の形になるわけです。
ベクトル三重積の括弧の順番を変えたものは、前述の交代性の性質により証明できます。まず、括弧の部分と次の部分を入れ替えてしまいます。すると、既に得られている結果を使えます。
$$(\overrightarrow{A}×\overrightarrow{B})×\overrightarrow{C}=-\overrightarrow{C}×(\overrightarrow{A}×\overrightarrow{B})=-\{(\overrightarrow{C}\cdot\overrightarrow{B})\overrightarrow{A}-(\overrightarrow{C}\cdot\overrightarrow{A})\overrightarrow{B}\}$$
$$=-(\overrightarrow{B}\cdot\overrightarrow{C})\overrightarrow{A}+(\overrightarrow{A}\cdot\overrightarrow{C})\overrightarrow{B}$$
ここで、内積の順序に関しては可換なので、書く文字の順番の入れ替えをしただけです。外積の順序の入れ替えをする時には符号が入れ替わります。
外積ベクトルに対する微分
外積ベクトルを微分すると、通常のスカラー関数の積に対する微分公式と似た形の式が成立します。この微分操作は、物理学などでの「時間微分」として使われる事があります。
$$\frac{d}{dt}(\overrightarrow{A}×\overrightarrow{B})=\frac{d\overrightarrow{A}}{dt}×\overrightarrow{B}+\overrightarrow{A}×\frac{d\overrightarrow{B}}{dt}$$
外積ベクトルの部分の順番に注意。逆にすると符号が変わってしまいます。
足し算の部分は逆にしても大丈夫。
この式は自明ではないので(スカラー関数の積の微分公式を知っていたとしても)、証明が必要になります。
この公式も、外積ベクトルの成分表示を使う事で示すことができます。ベクトルの微分は、各々の成分に対する微分として定義されます。ここでは、ベクトルの成分は全てスカラー関数であるとします。計算としては通常の積の微分公式を使用します。
$$x成分の微分:\frac{d}{dt}(a_2b_3-a_3b_2)=\left(\frac{da_2}{dt}b_3+\frac{db_3}{dt}a_2\right)-\left(\frac{da_3}{dt}b_2+\frac{db_2}{dt}a_3\right)$$
$$=\left(\frac{da_2}{dt}b_3-\frac{da_3}{dt}b_2\right)+\left(\frac{db_3}{dt}a_2-\frac{db_2}{dt}a_3\right)=\left(\frac{da_2}{dt}b_3-\frac{da_3}{dt}b_2\right)+\left(a_2\frac{db_3}{dt}-a_3\frac{db_2}{dt}\right)$$
これは確かに公式の外積ベクトルの和の形になっています。最後の変形は、外積ベクトルの成分となる事を明確にするために積の部分の順番を入れ替えただけです。(この式中に出てくるのは全てスカラー量なので、積の順序に関して可換です。)
同様にして、y成分とz成分についても示せます。
$$y成分の微分:\frac{d}{dt}(a_3b_1-a_1b_3)=\left(\frac{da_3}{dt}b_1-\frac{da_1}{dt}b_3\right)+\left(a_3\frac{db_1}{dt}-a_1\frac{db_3}{dt}\right)$$
$$z成分の微分:\frac{d}{dt}(a_1b_2-a_2b_1)=\left(\frac{da_1}{dt}b_2-\frac{da_2}{dt}b_1\right)+\left(a_1\frac{db_2}{dt}-a_2\frac{db_1}{dt}\right)$$
このようにして証明ができるわけです。