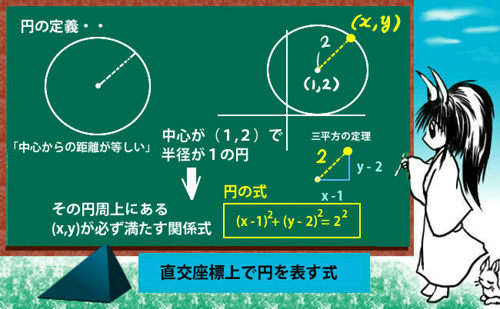
直交座標上で円を表す式について説明します。
基本となるのは図形としての円の定義と、三平方の定理(2点の距離)です。
1点からの距離が等しい点の集合:円
y=2xなどの1次関数は直交座標上で「直線」になり、y=x2などの2次関数は「放物線」になります。
では具体的に他の特定の図形、
例えば「円」の形になるように直交座標上での式を考えるとしたらどのようになるでしょうか。
結論を言うと次のようにします:
点(a,b)を中心とする半径rの円は、
(x-a)2+(y-b)2=r2 で表される。
これは何を言ってるのかというと「点(a,b)から点(x,y)までの距離がrですよ」という事です。これを満たす点(x,y)は点(a,b)を中心とする半径rの「円周上」に必ずありますよ、という意味です。
平面幾何での円の定義を思い出してみると、円とは「1点からの距離が等しい点の集まりで構成される図形」でしたから、これは適切という事になります。
そして2点間の距離は三平方の定理を使って出せばよいので、上記のような2乗を含んだ式になるわけです。特に原点を中心とする場合はx2+y2=r2という形になります。
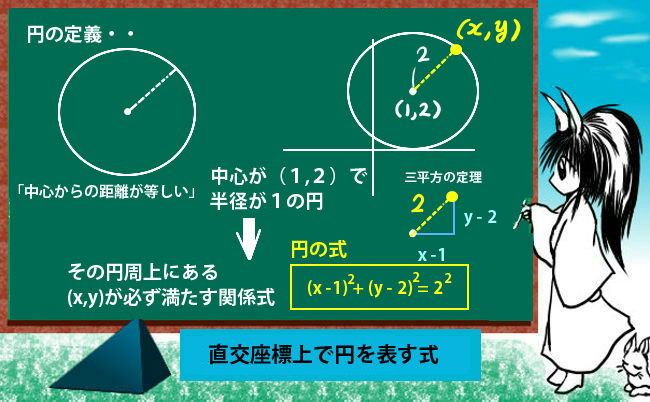
この時、(x-1)2+(y-2)2=4のような形で、右辺が2乗の形として明示しなくても円の式を表します。この場合には4=22のように書けるので、(1,2)を中心とする半径「2」の円という事です。
理屈自体は以上で終わりで、意味さえ理解すれば難しいものではないと思います。
そのうえで、高校数学でさらに問われる内容をいくつか挙げます。
まず1つは、関数y=f(x)の形で円を表すとどうなるかという事です。
上記のx2+y2=r2のような形も、一応関数の仲間ですがこのようなF(x,y)=0の形の式を「陰関数表現」と言ったり、その中のyを「陰関数」と言ったりします。逆にy=f(x)の形になっている事は「陽」に表わされていると言う事があります。
円の式の場合は、式を変形してy=f(x)の形にする事は比較的容易です。次のようになります。
$$原点中心の場合:x^2+y^2=r^2\Leftrightarrow y=\pm \sqrt{r^2-x^2}$$
$$一般の場合:(x-a)^2+(y-b)^2=r^2\Leftrightarrow y-b=\pm \sqrt{r^2-(x-a)^2}\Leftrightarrow y=\pm \sqrt{r^2-(x-a)^2}+b$$
プラスマイナスの符号は、原点中心の円であればx軸を境にした円の上側か下側かであるかを言っています。積分で円の面積を計算する場合などは、この形の式を使います。
ただし、図形同士の交点を調べる場合などは、無理にy=・・の形にしないで2乗の形のままで計算したほうが楽である場合も多いです。

円と図形との交点問題
円x2+y2=22と直線y=x+1の交点の数を調べる場合、円の式のyに直接y=x+1を代入して2次方程式の形にして実数解がいくつあるか調べるといった形になります。
グラフを描くと「明らか」である場合もありますが、式で示すなら次のようになります。
x2+y2=22にy=x+1を代入して、
x2+(x+1)2=4
⇔2x2+2x-3=0
ここで2次関数2x2+2x-3はx軸と2交点を持つので(x=0で負の値なので)2次方程式の解は実解が2つあり、円と直線の交点は2つというわけです。もし2次方程式が重解を持てば円と直線は「接する」という事になります。この計算をよく見ると、計算方法自体は放物線の時とほぼ同じという事も分かります。
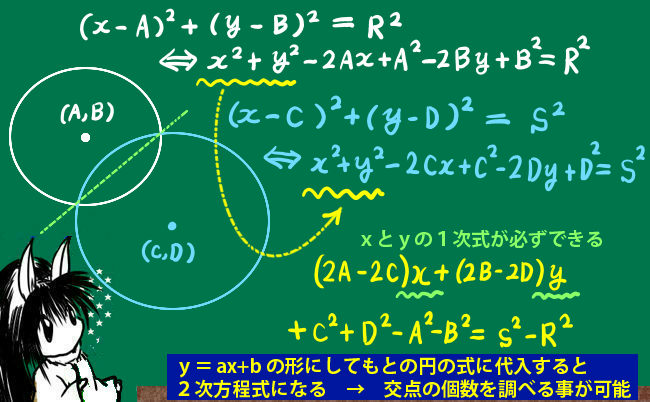
さて、では円同士の交点の場合はどうなるでしょうか。
この場合、直線と放物線との関係の場合と異なり、y=・・の形を代入しようとするとかなり面倒です。そのため、結論を言うと2乗を含んだままの形でまず処理し、1次式の形にする工夫をします。
具体例で見てみましょう。
■問い:2つの円(x+1)2+(y-1)2=3と(xー1)2+(y+1)2=7があるという。
これら2つの円の交点はいくつありますか。
この場合、どちらの式にもx2、y2の項とx、yの項がともにあります。
これらをどう処理すればよいかという話です。
まず、片方の円の式からx2+y2=・・の形にします。
(x+1)2+(y-1)2=3
⇔ x2+2x+1+y2-2y+1=3
⇔ x2+y2=2y-2x+1
これを、もう片方の式に代入します。
まず2乗部分を計算して、x2+y2の部分にまとめて代入するという事です。
(x-1)2+(y+1)2=7
⇔ x2+y2-2x+1+2y+1=7
これにx2+y2=2y-2x+1を代入して、
(2y-2x+1)-2x+1+2y+1=7
⇔ 4y-4x+3=7
⇔ y=x+1
ここで得られたyとxの1次式の関係は何を意味するかというと、特に「2交点を持つ場合」にはその2点を通る直線になります。このy=xの関係を、2つの円のどちらにでもいいので代入します。ここでは最初のほうの円に代入します。
(x+1)2+(y-1)2=3にy=x+1を代入して、
(x+1)2+x2=3
⇔ 2x2+2x-2=0 ⇔ x2+x-1=0
この2次方程式は異なる2実解を持つので、
2つの円は異なる2つの交点を持ちます。【解答】
尚、ここでもし交点を持たない(最後の2次方程式の形で実解を持たない)場合には、途中で得られる1次式の関係はもちろん2交点を結ぶという意味は持ちません。
また2交点を持つと分かった時の具体的な座標は、xが分かった時点でy=xの1次式のほうにxを代入すればyが分かるのですが、xをもしも円のほうに代入してyを出そうとするとさらに2つの解が出てくる場合があります。これは、直交座標上の円には端っこの2点を除いて、1つのx座標に対応する点が必ず2つ存在するからです。その時には片方の点だけが2交点の1つになります(2交点を結ぶ直線がx軸に垂直の場合を除きます。)
特定の点を通る円
少し面倒くさいタイプの高校数学の問題として、「ある1点を通る円」「ある2点を通る円」などが扱われる場合があります。
特定の点(A,B)を通る半径Rの円の場合、
中心の座標を(rx,ry)とすると (rx-A)2+(ry-B)2=R2という関係式ができますから、中心の座標を動かせるとすれば「軌跡は (A,B)を中心とした『半径R』の円」という事が言えます。
では「ある2点を通る円」ではどうなるかというと、半径が一定であれば図を描くとおそらく「2パターン」しかあり得ない事が予想できますが、実際そうなるのです。
(A,B)と(C,D)の2点を通り、半径がR、中心の座標を(rx,ry)とすると
(rx-A)2+(ry-B)2=R2 および
(rx-C)2+(ry-D)2=R2の2式ができます。
そこから先の計算は、まずrx2+ry2=・・の形の式に変形して、もう片方に代入します。すると、rxとryの1次式の関係を作れます。これは、(A,B)と(C,D)の2点を通る直線の式です。要するに、円同士の交点を調べる時の計算と同じです。
さらにry=・・の形を円のどちらか片方の式に代入すれば2次方程式になりますから、半径一定のもとで実数解は多くても2つ、つまり中心の座標は2パターンだけで他はあり得ないという事が式でも示されます。
(ここで、半径が小さすぎてそもそも所定の2点を通りようがない場合には実解がない結果になります。また、重解になる場合は2点のちょうど中点に円の中心が来る場合です。)
この場合に途中の計算で出てくるxとyの1次式は、(A,B)と(C,D)を結ぶ線分に垂直で、線分の中点を通る直線になります。
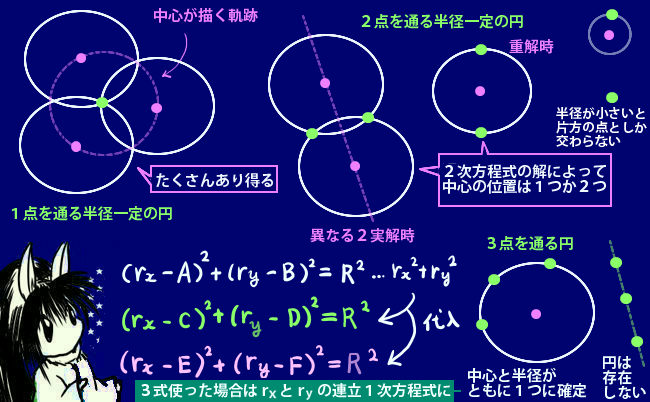
では、「3点を通る場合」はどうでしょう?この場合、中心と3点の関係を表す式が3つできます。いずれも、中心を動かせるとすると「円の式」の形になります。この時、まず1つを使ってrx2+ry2を残り2式のそれぞれに代入し、2乗を消して1次式の関係にします。
ところが、この場合は1次式の関係が2つできて「連立一次方程式」になってしまいますから、
rxとryが満たす解があるとすれば1つという事になります。
この時、異なる2点を通る場合と違うのは、rxとryの値を計算する時に円の半径は必要ないという事です。異なる2点を通る場合には、最後の2次方程式に半径が必要です。
それに対して異なる3点を通る場合には半径が「消えた」状態でrxとryの連立一次方程式が出てきます。
式で書くと、まず(rx,ry)と3点までの距離が等しいという3式を考えます。
(rx-A)2+(ry-B)2=R2
(rx-C)2+(ry-D)2=R2
(rx-E)2+(ry-F)2=R2
第1式から
rx2+ry2=2Arx-A2+2Bry-B2+R2 であり、
これを第2式と第3式の両方に代入します。
すると、
2(A-C)rx-A2+C2+2(B-D)ry-B2+D2=0
2(A-E)rx-A2+E2+2(B-F)ry-B2+F2=0
という2つの式になりますが、この時点でRは消えているわけです。
これは最初の3式でともに「等しい距離R」を使ったためです。
(一見ごちゃごちゃした式ですが、rxとryに関して見れば1次式です。)
そこで連立1次方程式からrxとryを確定させると、もとの式に代入すると半径であるRもそれによって決まらないとおかしい話になります。つまりこの場合は、中心座標が1つに決まる事に加え、半径も1つに決まるという事です。
ここでじつはもう1つ細かい注意点があって、
それは連立1次方程式は「解を持たない」場合があるという事です。
「そんな場合ありましたっけ。」と思われるかもしれませんが、単純な話で、
x+y=2 かつ
x+y=3
のような場合の事です。
これは、ここでは異なる3点が「同一直線上」にある場合に発生します。ですので、その場合に限っては最後の連立1次方程式の解がないので、3式を満たすrxとryは「存在しない」という事になります。
まとめると、「『同一直線上にない』異なる3点」を通る円はただ1つしかなく、しかも半径も1つに確定するという事になります。また、同一直線上にある異なる3点を通る円は存在しないという事にもなります。