逆三角関数とは「三角関数の逆関数」で、正弦、余弦、正接のそれぞれに対して存在し、
それぞれ「逆正弦関数」「逆余弦関数」「逆正接関数」と呼んで Arcsinx,Arccosx,Arctanx
もしくは sin-1x,cos-1x,tan-1x のように書きます。
あるいは arcsinx,arccosxのように書く事もできますが、
それらは記述法によっては Arcsinx等と区別して意味を持たせる事もあります。
逆三角関数が使われる事が比較的多いのは微積分においてです。そのため、この記事の後半では微積分的な内容がやや多くなります。また、どちらかというと数学的な内容が中心になりますが逆三角関数のいくつかの使用例についても説明します。
※三角関数のベキ乗は、習慣的に(sinx)2=sin2xのように書かれます。
しかし、一般的にはsin-1xは逆正弦関数(=正弦関数の逆関数)であって、
1/(sinx)を意味しない事が多いです。
一般的に、三角関数の逆数に関しては1/(sinx)=(sinx)-1(=cosecx)
と書き、
負のベキ乗(あるいは逆数のベキ乗)に関しては
{1/(sinx)}2=1/(sin2x)=(sinx)-2(=cosec2x)などのように書きます。
一般的に、f(x)の逆関数はf-1(x)と記します。
表記体系としては一応 sin-1xを1/sinxと勘違いしないようにはなっていますが、
当サイトでは基本的に逆三角関数は Arcsinxや Arccosxの表記を使用しています。
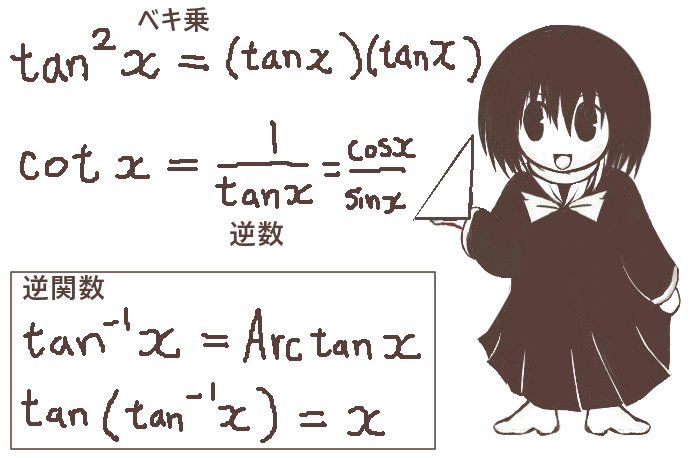
また、「余接(cot)」「正割(sec)」「余割(cosec)」などは三角関数の「逆数」です。
例えばsecθ=1/(cosθ)であって、それらは「逆三角関数」とは別物になります。
余接関数等にも逆関数を考える事はできますが、正弦・余弦・正接の逆三角関数と比べると使用頻度は低いと言えます。
種類と基本的性質
通常の正弦関数y=sinxに対してはxの値を決めればyが定まるわけですが、理論的にはyに対してxの値も計算できるというふうにも見れます。つまりx=f(y) のように考えるわけです。これが一般的な逆関数の考え方ですが、それを三角関数について考えたものが逆三角関数です。
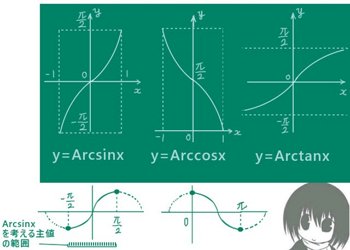
- y=sin xの時、x=Arcsiny(もしくはsin -1y)と書き、逆正弦関数と呼びます。
- y=cosxの時、x=Arccosy(もしくはcos-1y)と書き、逆余弦関数と呼びます。
- y=tanxの時、x=Arctany(もしくはtan-1y)と書き、逆正接関数と呼びます。
Arcsinxと書く場合は、「アークサインエックス」のようにも読む事があります。
同様にArccos, Arctan は「アークコーサイン」「アークタンジェント」と読みます。
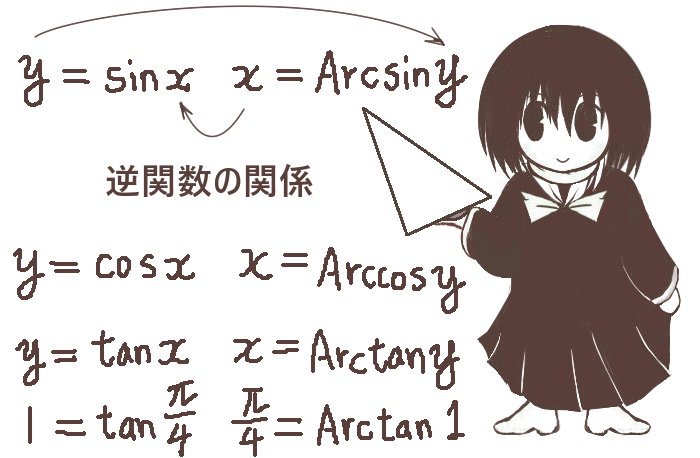
例えばy=sinxに対して
x=π/2の時にはy=sin(π/2)=1であるので、π/2=Arcsin1のようになります。
同様に、例えばx=π/4の時にtanx=1なので π/4=Arctan1のようになります。
つまり「三角関数あるいは三角比のある値を与える角度は何か?」
という事を表したのが逆三角関数です。
逆三角関数は通常の三角関数と違って、微積分に関して以外の関係式は多くありません。
例えば加法定理のような関係式は基本的に考えないわけです。(ただし通常の三角関数の加法定理と組み合わせて計算をする事はあります。)
積分の時に一応覚えていると良いかもしれない関係式としては
Arcsinx+Arccosx=π/2があります。
ただしこれは後述するように
逆三角関数の値として「主値」を採用する場合において成立するものです。
すなわち、Arcsinxの値域を [-π/2,π/2]として
Arccosxの値域を [0,π]とした場合に成立する関係式です。
ですので具体的な意味としては実は難しくないのですが、
数学的には注意点は2つほどあります。
- 逆三角関数を単独の関数として扱う時は、他の関数と同じく「xを変数として」
y=Arcsinxのように書くのが普通です。(その時、siny=xです。)
通常の三角関数y=sinxに対して逆正弦関数を考えるならx=Arcsinyとも書きます。
ただし文字自体は変数をxとしてもyとしても、本質的にはどちらでも変わりません。 - 三角関数は周期関数なので
y=sinxなどにおいてyの値に対して複数の(無限個の)xの値があり得ます。
例えばx=π/4の時にtanx=1となるのは「x=π/4もそうだがx=9π/4もそうである」といった話にもなるという事です。
そのために逆三角関数を考える時には通常、1周期分だけを考えて
特に0を含む値域(三角関数で言えば定義域)を単調関数になるように選んで使うのが普通です。逆三角関数がその範囲の値である事を指して主値と呼びます。
yとxの文字の使い分けの関係は混乱を生じやすいかもしれませんが、
何の文字を使っているかに関わらずに Arcsin 等の逆三角関数を使う時には
変数とその定義域は「通常の三角関数の値」であり、
逆三角関数の値とその値域は「角度」を考えています。
多くの場合、三角関数y=sinxなどを使っている中で逆三角関数を考える場合には
変数と関数を表す文字を区別するためにx=Arcsinyのように書いて、
微積分などで単独で逆三角関数を最初から使う時にはy=Arcsinxのように書いたりします。
(後述で少し触れますが同じく逆関数の関係にある指数関数と対数関数の関係と同じように捉えると分かりやすいかもしれません。)
文字としてはxでなくてもθなどを使っても同じです。
逆三角関数の「主値」について
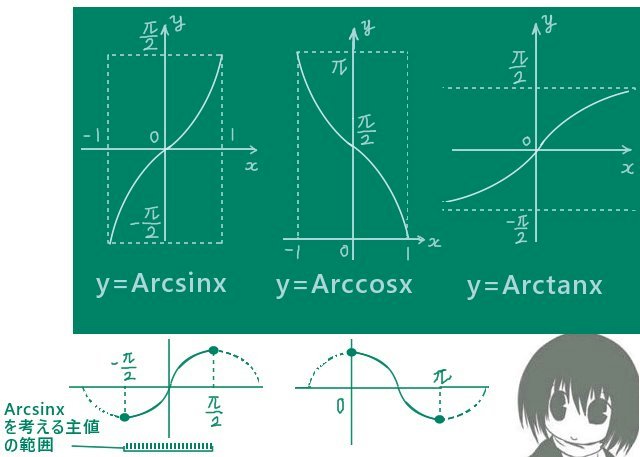
逆三角関数の変数の定義域および値域としての「三角関数の1周期分」については無限個の区間からどこを切り取っても同じですが、普通は逆三角関数が単調増加または単調減少となるように考えます。
例えば sinx に対しては [-π/2,π/2]で考えれば十分とするわけです。(これは三角関数の定義域で、逆三角関数から見れば値域になります。)
また、普通は三角関数の1周期分を0を含む範囲で考えて、先ほども触れましたが逆三角関数の値がそこに含まれる事を指して主値と呼ぶ事があります。例えば sinx=0となるxは0,π、2π、・・・のように無限にあり得るわけですが、主値を使うなら Arcsin0=0です。
何のことわり書きも無ければ、普通は逆三角関数は主値で考えられています。
逆三角関数として「主値以外の一般の値」も含めている場合は 「arcsinx」のように書くと決めている表記法もあります。
ただし逆三角関数と言えば普通は主値を考えるので、どの表記法が正しい間違っているの問題ではありませんが、当サイトでは「断り書きがなければ逆三角関数は主値を考える」ものとして、表記方法は特別な意味をこめずArcsinxのように書くという事にします。
- 逆正弦関数 Arcsinx の値域:[-π/2,π/2]
- 逆正弦関数 Arccosxの値域:[0,π]
- 逆正接関数 Arctanxの値域:[-π/2,π/2]
他方で、定義域では Arcsinx と Arccosx については [-1,1]であり。
Arctanxの定義域は (-∞,+∞)です。
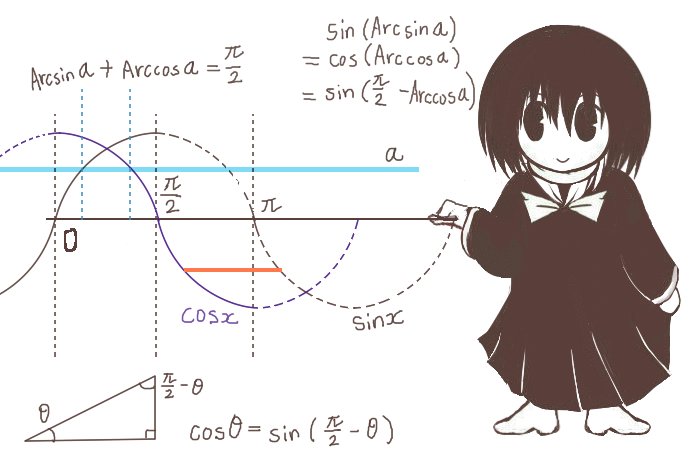
3つの逆三角関数で共通して主値で値を考える場合には、
同じ三角関数の値x(これは変数ではなく関数値)に対するArcsinxとArccosxについて
sin(Arcsinx)=cos(Arccosx)=sin(π/2-Arccosx)であり、
Arcsinx=π/2-Arccosx ⇔ Arcsinx+Arccosx=π/2の関係式が成立します。
ここで主値におけるArccosxの値域は [0,π]、でArcsinxの値域が [-π/2,π/2]なので
範囲の整合性はとれているわけです。
主値で考える時には次式が成立します。$$\mathrm{Arcsin}x+\mathrm{Arccos}x=\frac{\pi}{2}$$
初等関数としての逆三角関数の位置付け
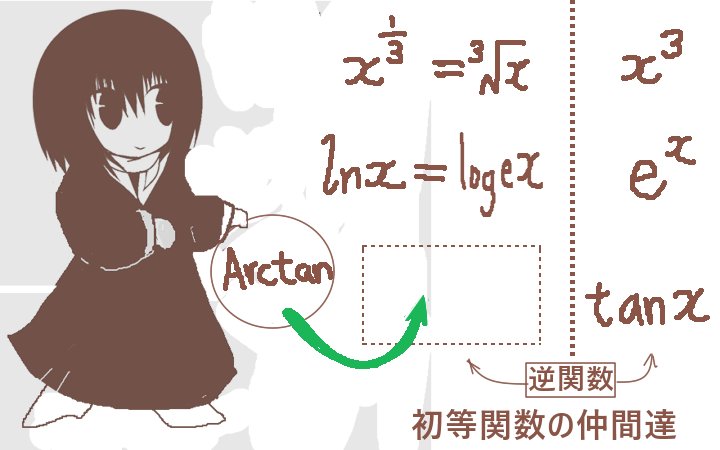
逆三角関数は、分類としては実は初等関数に含まれます。
少し妙に思えるかもしれませんが、一応それには理由があります。
初等関数とは、程度の低い関数という意味では無くて数学において基礎となっていて非常に多く使う種類の関数をまとめて呼ぶ総称です。そこに実は逆三角関数も含まれるわけです。(初等関数に対する語は「特殊関数」です。多くは積分や級数で表され、ベータ関数、ガンマ関数、ゼータ関数など多数あります。)
具体的には、次の関数およびその四則演算(平方根なども含む)と逆関数、合成関数を指します。
- 単項式xa(aは実数)
- 三角関数 sinxなど
- 指数関数 exなど
さてここで「対数関数」lnx=logexを敢えて入れませんでしたが、対数関数も初等関数の1つです。ただし、対数関数は指数関数の逆関数です。(指数関数が対数関数の逆関数であると言っても正しい。)そのため、同じ初等関数の中でそれら2つは対になっているわけです。
【双曲線関数 sinhxなども初等関数の1つですが、指数関数によって定義されます。】
また、単項式についてもxaとx1/aが互いに逆関数の関係になっています。
例えばx≧0におけるy=x2の逆関数はy=x1/2=\(\sqrt{x}\) です。
「逆数」と「逆関数」の違いに注意すると、逆三角関数での話との関連が見えるでしょうか。
y=xの逆数はy=1/x=x-1ですが、逆関数は全く同じ形のy=xです。y=x2の逆関数はx≧0の範囲でy=x1/2になりますが、それに対してy=x-2=1/(x2)です。
また逆三角関数の値域の話と同様に、
何の条件もなくy=x2に対してxについて解くとx=\(\pm\sqrt{y}\) であり、解が2つがあり得るわけですがx≧0のような制限があるとプラスの値だけに決まります。
そこで「じゃあ三角関数の逆関数ってどういうものか?」というところにつながるわけです。
指数関数にも単項式にも逆関数を考える事ができて、それではつまり、初等関数という枠組みで見ると三角関数だけ逆関数を敢えて考えない数学的な理由は無くて、むしろ考えておいたほうが整合性が色々ととれる事になります。
ただし、指数関数と対数関数の関係のように逆三角関数にも単独で積極的に活用できる性質があるのかというと、他の初等関数と比べるとそういう面は「やや弱い」と言えそうです。
確かに逆三角関数の性質として「角度が値として分かる」というのはあるのですが、そもそも角度というものが特別ないくつかの値以外は把握も測定もしづらいところがあるから三角比や三角関数を考えているのでもあります。
しかし次に見るように、微分と積分について考えると少なくとも数学上の活用方法は出てきます。
逆三角関数の微分の公式
値域を主値で考えた時の逆三角関数の微分公式を挙げておきます。(ただし、微分そのものが積極的に使われるというよりは、むしろその逆演算である積分のほうでの使い道がやや多いです。)
Arcsinxの微分などと聞くといかにも面倒くさそうですが、実は三角関数の微分に対して逆関数の微分公式を適用するとすぐに導出できるのです。xやyの変数の扱いにだけ注意すれば意外と難しくないのではないかと思います。
通常の三角関数の微分によって得られる導関数はそれぞれ次のようになります。
- (d/dx)sinx =cosx
- (d/dx)cosx=-sinx
- (d/dx)tanx =1+tan2x=1/(cos2x)
これらに対して逆関数の微分公式を使うと、変数の表記方法に注意して3つの逆三角関数の微分公式を導出する事ができます。
逆三角関数の値を主値で考えた時、微分による導関数は次のようになります。
■逆正弦関数 Arcsinx の導関数
$$\frac{d}{dx}\mathrm{Arcsin}x=\frac{1}{\sqrt{1-x^2}}$$
■逆余弦関数 Arccosx の導関数
$$\frac{d}{dx}\mathrm{Arccos}x=-\frac{1}{\sqrt{1-x^2}}$$
■逆正接関数 Arctanx の導関数
$$\frac{d}{dx}\mathrm{Arctan}x=\frac{1}{1+x^2}$$
ArcsinxとArccosxに関してはx≠-1かつx≠1のもとで考えます。
Arcsinx と Arccosx については定義域は [-1,1]ですが
微分を考える時はx=±1を除いて (-1,1)の範囲だけで考えます。
その範囲内では平方根の中身は必ずプラスの値になります。
また、よく見ると導関数が定義できる範囲でArcsinx と Arctanx の導関数は常にプラスの値で
Arccosx の導関数は逆に常にマイナスの値です。
実際 Arcsinx と Arctanxは主値を考える時の値域[-π/2,π/2]で単調増加関数であり、
逆に Arccosx は主値を考える時の値域[0,π]において単調減少関数です。
これらの公式は比較的簡単な計算により導出できます。
Arcsinx と Arccosxの導関数が符号だけの違いである理由も導出の過程を見ると分かるでしょう。
計算の注意点としては例えば逆正弦関数ではy=Arcsinxとした時、siny=xであるので逆関数の微分公式にもそれを当てはめる必要があるといった事です。
$$\frac{d}{dx}\mathrm{Arcsin}x=\frac{1}{\frac{d}{dy}\sin y}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin ^2y}}=\frac{1}{\sqrt{1-x^2}}$$
$$\frac{d}{dx}\mathrm{Arccos}x=\frac{1}{\frac{d}{dy}\cos y}=-\frac{1}{\sin y}=\frac{1}{\sqrt{1-\cos ^2y}}=\frac{1}{\sqrt{1-x^2}}$$
$$\frac{d}{dx}\mathrm{Arctan}x=\frac{1}{\frac{d}{dy}\tan y}=\frac{1}{1+\tan^2y}=\frac{1}{1+x^2}$$
ArcsinxとArccosxの微分の途中の計算では sin2x+cos2x=1の関係を使っています。
Arctanxの微分においては、途中計算では微分の公式以外には特に何も使わずに
y=Arctanx から tany=xであるという関係だけを使っています。
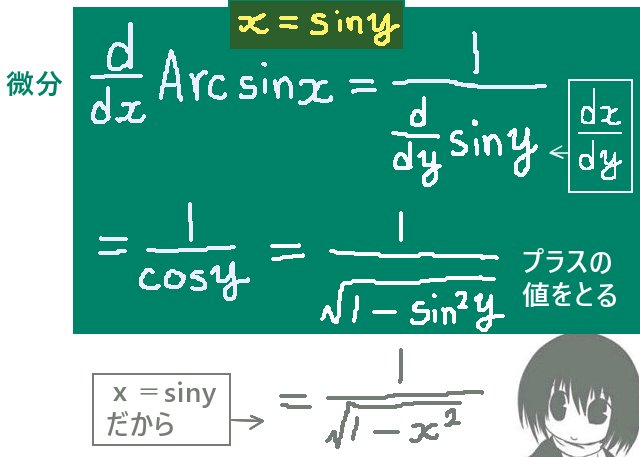
この導出の過程でArcsinxの導関数については cosy=\(+\sqrt{1-\sin^2y}\)のように考えています。(マイナスではなくプラスの値としています。)これはArcsinxを主値で考えており、
値域(三角関数から見れば定義域)を [-π/2,π/2]として考えているためです。
その範囲ではcosy≧0となります。(ただしここではxosy=0となる端点を除いています。)
他方でArccosxについては値域を [0,π]として考えているのでその範囲ではsiny≧0です。
(先ほどと同じく実質はsiny>0で考えます。)
ゆえにsiny=\(+\sqrt{1-\cos^2y}\)としています。
逆三角関数に限らず、逆関数一般について次の関係式が成立します。
$$\frac{dy}{dx}=\frac{1}{\Large{\frac{dx}{dy}}}$$
この式を実際の計算で使う時にはyとxの関係について注意が必要です。
y=Arcsinxの時にはx=sinyですから、yをxで微分した時に逆関数の微分公式での分母は「x=sinyをyで微分した導関数」つまり cosyが入ります。
逆三角関数の積分の公式
さて、微分が分かれば積分のほうも分かる事になりますが、逆三角関数の導関数は意外にも「式としては三角関数が全然関係ない」という形になっています。ですので図形問題や三角関数を考えているわけではなくても積分に使える場合があるのです。
平方根の中身が0より大きくなる定義域において、次の積分公式が成立します。
$$\int \frac{1}{\sqrt{1-x^2}}dx=\mathrm{Arcsin}x+C$$
$$\int -\frac{1}{\sqrt{1-x^2}}dx=\mathrm{Arccos}x+C$$
$$\int \frac{1}{1+x^2}dx=\mathrm{Arctan}x+C$$
$$\int \sqrt{a^2-x^2}dx=\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}\right)+C$$
Cは任意の実数定数です。
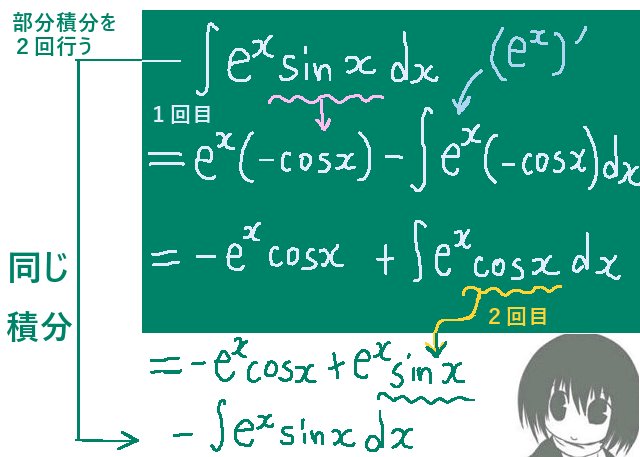
4番目の式については部分積分の公式を使って導出するもので、実用性は別問題として
「逆三角関数を使って原始関数を表せる」という例です。(置換積分でも計算は可能。)
このような形の関数の積分を考える時には置換積分や部分積分を考える必要はなくて、そのまま逆三角関数を当てはめる事ができます。
これらの積分の式について原始関数が Arcsinxと Arccosxになる2式を特に見比べると、
被積分関数が符号だけの違いとなっています。
ここで「符号が違うだけで積分の結果が変わるものか?」と妙に思えるかもしれませんが、
Arcsinx=-Arccosx+π/2の関係があるので、Arcsinxと Arccosxは互いに変換が可能です。
不定積分においてはπ/2は任意定数に含める事ができるので、Arcsinxのほうの不定積分の式の両辺に-1を乗じた場合には式としてはArccosxのほうの不定積分の式に変える事はできます。
例1:逆正接関数のマクローリン展開と角度計算
逆三角関数はある三角関数の値から角度を逆算できる関数ではありますが、関数としての実態が分からないと結局特別な値以外は簡単には計算できない事になってしまいます。
「それでも別に支障ない」と言ってしまえばそれまでですが一応、マクローリン展開(x=0におけるテイラー展開)を使えば逆三角関数の近似値をxから直接計算する事は可能です。
ただし、計算しやすい形になっているのは逆正接関数Arctanxのマクローリン展開ですので、
それについて説明をします。
展開式(無限級数展開)の内容
Arctanxのマクローリン展開は、意外かもしれませんが正弦関数や余弦関数のマクローリン展開に形は似ていて、式自体はそれほど複雑ではありません。
逆正接関数Arctanxはマクローリン展開可能(x=0でテイラー展開可能)であり、
|x|<1において次式で表す事ができます。
$$\mathrm{Arctan}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}-\frac{x^{11}}{11}+\cdots$$
(x=1においても一応この式は収束します。)
この式で、てきとうにx=1/5などどしてみると、
Arctanx=1/5-1/(53・3)+1/(55・5)-・・・
4項目以降はほぼ0であると考えると、
Arctanx=1/5-1/375+1/15625-・・・≒0.1974≒0.0628π
これは度数法で言うとおおよそですが180×0.06358≒11.3°です。
このような数値の計算は、計算ソフトや関数電卓で直接的に計算できるならそれを使えばよいという話でもあるのですが、一応このように計算もできるという事です。(また、ソフト等を使うにしても逆三角関数によって「角度」を計算できる事は理系の人であれば一応知っておいてもよいのではないかと思います。)参考までにおおよその値の例をいくつか挙げておきます。
| tanx | Arctanx(=弧度法での角度) | \(a\pi\)の形で表す時 | 度数法での角度 [ °] |
| 0.99 | 0.780 | 0.248\(\pi\) | 44.71 |
| 0.9 | 0.733 | 0.233\(\pi\) | 41.99 |
| 0.8 | 0.674 | 0.215\(\pi\) | 38.66 |
| 0.7 | 0.611 | 0.194\(\pi\) | 34.99 |
| 0.5 | 0.464 | 0.148\(\pi\) | 26.57 |
| 0.3 | 0.291 | 0.093\(\pi\) | 16.70 |
| 0.1 | 0.0997 | 0.032\(\pi\) | 5.711 |
尚、tan(π/4)=1ですので Arctan1=π/4≒0.786[rad]で、度数法では45°です。
また、0に近い角度であればArctanx≒xとも言えます。
ただし同じくマクローリン展開からsinx≒xも同様に分かるので、0に近い角度であれば通常の正弦関数で考えたほうがむしろ早い事にはなります。
参考までに、Arcsinxのマクローリン展開は |x|<1の範囲で次式のようになります。
これはArcsinxの導関数を2項定理によって展開する事で得られますが、Arctanxと比較して結構面倒な形だと言えそうです。$$\mathrm{Arcsin}x=x+\sum_{n=1}^{\infty}\left(\frac{1\cdot3\cdot5\cdots(2n-1)}{2\cdot4\cdot8\cdots(2n)}\frac{\large{x^{2n+1}}}{2n+1}\right)$$
Arctanxのマクローリン展開の導出
この式は、前述の微分公式を使って普通にマクローリン展開を考えて導出しようとすると、実は結構大変です。というのも、1階と2階の微分はよいとしても、3階、4階・・・と高階微分を計算していくと形が複雑になるためです。
しかし実は、1階の微分後に幾何級数展開(等比級数による展開)する事でArctanxのマクローリン展開は導出できるのです。また、それによって各高階導関数のx=0における微分係数も判明する事になります。(これは、そのように考えてよいという定理があります。)
まず(d/dx)Arctanx=1/(1+x2)であるわけですが、
|x|<1であればこれは幾何級数が収束する値として考える事ができて、
具体的には次のようになります。
1-x2+x4-x6+・・・=1+(-x2)+(-x2)2+(-x2)3+(-x2)4+・・・
これは、「公比が-x2である等比級数」「公比が-x2である等比数列の項数を無限大にした極限」と言っても同じです。
よって、|x|<1の範囲では(d/dx)Arctanx=1-x2+x4-x6+・・・
そこで、この関数については項別積分が可能なので(※無限級数に対して項別積分が可能であるのは「収束円の内部においてだけ」という条件が必要なので注意)、|x|<1のもとで各項を積分すると次のようになります。積分変数をtとして、0からxまでの定積分という形にします。
$$\int_0^x\left(\frac{d}{dt}\mathrm{Arctan}t\right)dt=\int_0^x\left(1-t^2+t^4-t^6+\cdots\right)dt$$
$$\mathrm{Arctan}0=0に注意すると\int_0^x\left(\frac{d}{dt}\mathrm{Arctan}t\right)dt=\mathrm{Arctan}xであるので$$
$$\mathrm{Arctan}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots$$
このようにして得られた級数は、実はマクローリン展開に等しくなります。
(無条件にではなく、ここでの場合はそうなります。)
無限級数に対して項別積分が可能であるかの数学的な問題を避けたい場合には、有限の和に対して積分をする方法もここでは適用できます。
S=1+(-x2)+(-x2)2+(-x2)3+(-x2)4+・・・+(-x2)n
両辺に-x2を乗じると次式です。
-x2S=(-x2)+(-x2)2+(-x2)3+(-x2)4+(-x2)5+・・・+(-x2)n+(-x2)n+1
両辺について1式目から2式目を引くと次式です。
(1+x2)S=1-(-x2)n+1
⇔S=1/(1+x2)-(-x2)n+1/(1+x2)
【そのため、|x|<1であればn→∞でS→1/(1+x2)】
ここで、敢えて極限を考えずに式を整理すると有限のnに対して
S+(-x2)n+1/(1+x2)=1/(1+x2)です。
そしてSに対して元の式を代入すると、
1/(1+x2)=1+(-x2)+(-x2)2+(-x2)3+・・・+(-x2)n+(-x2)n+1/(1+x2)
これは有限の項の和ですので、項別積分は可能です。
そこで項別積分を実施すると、有限の範囲でのマクローリン公式(x=0におけるテイラー公式)を作れます。その後で、積分型の剰余項の収束について考える必要があります。(結果は剰余項はn→∞で0に収束します。)
例2:ライプニッツ級数の導出
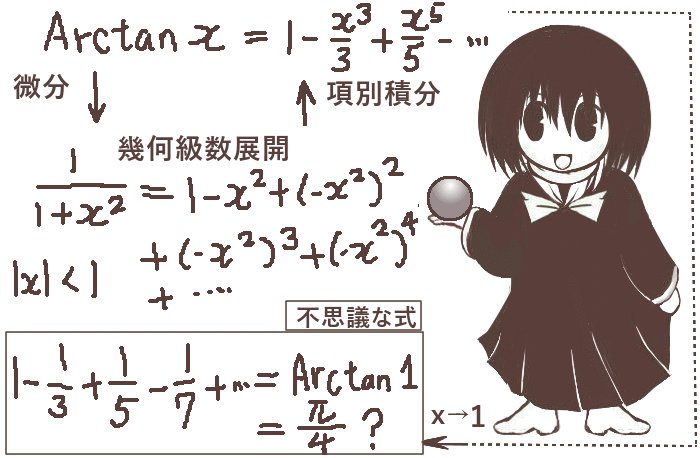
ライプニッツ級数とは、数学的に成立するという事以上の意味はそれほど無いとも言われますが円周率を無限級数で表す式です。さらに、各項は簡単な有理数で表されているという「不思議な式」です。
ライプニッツ級数を導出する方法は複数ありますが、実は逆正接関数を使う方法がその1つです。
次の無限級数は収束し、値は円周率の1/4倍になります。
$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+\cdots=\frac{\pi}{4}$$
これは「近似値」とは少し違うもので、「π/4を極限値として持つ」という意味において成立する「等式」になります。
ところで、この式に非常に似た形の式をこの記事内で先ほど考察していて、
それが逆正接関数 Arctanxのマクローリン展開です。実の所、Arctanxのマクローリン展開で
「x=1と置いたもの」はライプニッツ級数に他なりません。
それは偶然ではなく、きちんと証明できます。ただし Arctanxのマクローリン展開を幾何級数から導出する時には |x|<1の条件をつけていましたから、単純に「x=1を代入」するのは少し危ない操作であると言えます。もしかしたら、x=1では無限級数は無限大に発散するかもしれないからです。
しかし実際は、x→1とした時にもx-x3/3+x5/5-x7/7+・・・は収束します。
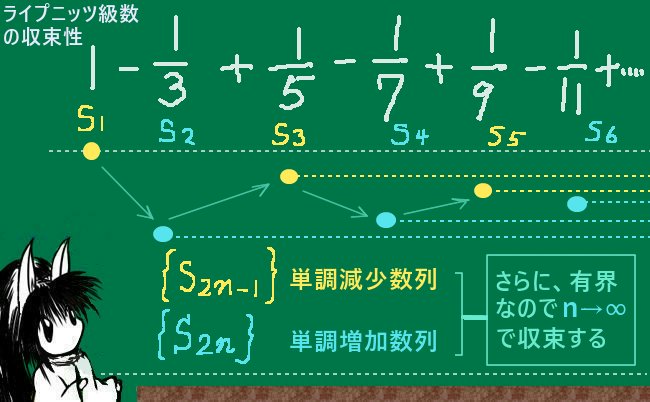
ライプニッツ級数が収束する事自体は実は比較的簡単な考察により分かる事で、n項目までの和Snについて奇数番目と偶数番目を分けて考える事で証明できます。
S2n-1に対してS2nはマイナスの項が加わって少し減りますが、S2n+1でまた少し増えます。しかし項の絶対値自体は減り続けるため、S2n-1の値までは戻りません。
よってS2n-1>S2n+1です。
すなわち奇数番目までの和だけに着目すると{S2n-1}は単調減少数列となっています。
逆に遇数番目までの和S2nに着目すると{S2n}は単調増加数列となります。
さらに、プラスとマイナスが交互に現れるので必ずS2n-1>S2nでもある事から
任意の自然数nに対してS2n<S2n-1<S1=1により{S2n}は上に有界であり、
S2n-1>S2n>S2=2/3であり、{S2n-1}は下に有界です。
つまり両者ともに有界な単調数列なので{S2n-1}と{S2n}はそれぞれ収束し、
さらにS2n-S2n-1を考えてみると各項の絶対値は0に近づいて行くので
n→∞でS2n-S2n-1→0です。
つまりn→∞で{S2n-1}と{S2n}は同じ値に収束します。
すなわち、級数全体も収束する事になります。(ただし、極限値はまだ不明です。)
この事は実はライプニッツ級数に限らず、プラスマイナスが交互に現れる交代級数について「項の絶対値が単調減少でn→∞で0に収束する」という条件があれば級数も収束するという定理があります。(ライプニッツの定理と呼ばれる事があります。)
Arctanx自体はx=1以上でも全実数において値を持ちます。Arctan1=π/4です。
(π/4は度数法で言えば45°の角度です。)
そこで|a| <1に対してπ/4-(a-a3/3+a5/5-a7/7+・・・)を考えます。
Arctan1=π/4であり、
|a| <1に対してはマクローリン展開により、
Arctan a=a-a3/3+a5/5-a7/7+・・・です。
よって、π/4-(a-a3/3+a5/5-a7/7+・・・)=Arctan1-Arctan a となります。
ここでa→1の極限を考えますが、
Arctanxは連続関数なのでa→1の極限ではArctan a→Arctan1です。
それは当然と言えば当然の関係ではあるのですが、
それによってマクローリン展開の式もArctan1に収束する事が分かります。
つまりはa→1で a-a3/3+a5/5-a7/7+・・・→π/4となるわけです。
「Arctanxが連続関数である事」の部分を少し詳しく見ると次のようになります。
まずtanxが連続関数であり、「狭義単調増加(x<wに対してf(x)<f(w)となる)または狭義単調減少であればその逆関数もまた連続であり、x=1においても連続」となります。
今、f(x)=Arctanxとするとx=1で連続であるから
「1を含むある開区間Uがあって、任意の実数ε>0に対してUの区間の長さを十分小さくすれば、Uに含まれる任意の実数xに対して |f(1)-f(x)|<εとなるようにできる」
という事になります。
つまり先ほどの|a| <1であるaについて任意の実数ε>0に対して
|f(1)-f(x)|<εとなる「1を含む開区間U」に含まれているものを選べば、
任意の実数ε>0に対して|f(1)-f(a)|
=|Arctan1-Arctan a|= |π/4-(a-a3/3+a5/5-a7/7+・・・)|< ε
よって、a→1の極限では
a-a3/3+a5/5-a7/7+・・・→ π/4という事になります。
さてここで、「aを1に置き換えて1-1/3+1/5-1/7+・・・=π/4」としても大体合っているのですが、より正確にやるのであればここでは概略だけに留めますが次の定理を使います。おそらく聞き慣れないかもしれませんが、連続性定理とかアーベルの連続性定理などと呼ばれます。
$$(-\rho,\rho)で収束する\sum_{n=0}^{\infty}a_nx^nがある時$$
$$\sum_{n=0}^{\infty}a_n\rho^nも収束する\Rightarrow\lim_{x\to{\rho -0}}\sum_{n=0}^{\infty}a_nx^n=\sum_{n=0}^{\infty}a_n\rho^n$$
ρ( >0)は「収束半径」、開区間(-ρ,ρ)は「収束円」とも言います。
極限「x→ρ-0」は「左極限」(もしくは「左側極限」)を表し、
「ρよりも小さい値として近づく」という意味を持ちます。
この定理は一体何を言っているのかというと、ここでの話で具体的に言うと
まず|x|<1でマクローリン展開により
Arctanx=x-x3/3+x5/5-x7/7+・・・となるのでこの級数は収束しています。
次にx=1の時に相当する式である1-1/3+1/5-1/7+・・・は
収束する事が個別の考察で分かっている状況です。しかし極限値は不明です。
そこで連続性定理によれば
1-1/3+1/5-1/7+・・・の極限値は
x-x3/3+x5/5-x7/7+・・・
の左側極限x→1-0の極限値に等しいという事になります。
そして、x-x3/3+x5/5-x7/7+・・・のx→1-0の時の極限値は
Arctanxの連続性によりArctan1=π/4という事が分かっているので、
1-1/3+1/5-1/7+・・・=π/4という結果を得るという流れです。
$$|x|<1 で\mathrm{Arctan}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdotsであり、収束する。$$
$$x=1に相当する1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+\cdotsは収束する事が示されている。$$
$$今、\mathrm{Arctan}xの連続性により\lim_{x\to{1-0}}\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\right)=\mathrm{Arctan}1=\frac{\pi}{4}$$
$$連続性定理により1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\lim_{x\to{1-0}}\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\right)$$
$$=\mathrm{Arctan}1=\frac{\pi}{4}$$
ライプニッツ級数を導出する他の方法としては、4分円(円の1/4)の面積を積分で計算する方法があります。ただし通常のx軸方向の積分ではなく、y軸を利用した少し工夫が凝らされた計算になります。実はその場合でもArctanxのマクローリン展開を考えた時と同様に幾何級数展開による計算を行います。
例3:マチンの公式による円周率の表現
再び数学的な話ではありますが、円周率を表す式は実は1つではなくたくさんあります。ライプニッツ級数は「その1つ」であり、不思議な式ではありますが「収束の速さが遅い」事でも実は知られています。収束の速さが遅いという事は、直接計算してもなかなか「3.14・・・」が出てこない事を意味します。
他方で収束が速い円周率の公式も知られていて、その1つがマチンの公式という逆三角関数で表されるものです。ここでは通常の三角関数における正接の加法定理を使った証明方法を簡単に説明します。
次の式で円周率を表せるという事が知られています。
$$4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)=\frac{\pi}{4}$$
これもライプニッツ級数同様に「等式」として成立する関係式であり、
さらにこの式に関しては極限の計算などは特に必要としません。
ここではこの奇怪な式が「確かにπ/4に一致する」事の確認を優先する形で証明を述べます。
最初に結論を言うと、マチンの公式の左辺は正接関数に対する「角度」であり、その角度を持つ正接の値が1になる事で「角度=π/4」という事が言えます。
$$示すべき式:\tan\left(4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)\right)=1$$
普通の角度で考えるなら tan(4θ1+θ2)=1となる事を証明する事になります。
加法定理を使うと、tan(4θ1+θ2)={tan(4θ1)-tanθ2}/[1+{tan(4θ1)}(tanθ2)}ここで、少し面倒ですが4θ1に対して倍角の公式(加法定理でも同じ)を2回使います。
tanθ1=1/5とすると上手く行くのでその値を代入します。
$$\tan(2\theta_1)=\frac{2\tan\theta_1}{1-\tan^2\theta_1}=\frac{2}{5}\cdot\frac{25}{24}=\frac{5}{12}$$
再度、倍角の公式を使います。具体的な数値を入れます。
$$\tan(4\theta_1)=\frac{2\cdot\frac{5}{12}}{1-\left(\frac{5}{12}\right)}=\frac{5}{6}\cdot\frac{144}{119}=\frac{120}{119}$$
これを、最初のtan(4θ1+θ2)={tan(4θ1)-tanθ2}/[1+{tan(4θ1)}(tanθ2)}に代入します。
θ2の値は結論から言えば1/239ですが、ちょっとここでは「確かにその値にすればよい」という事を式を解く形で見てみる事にしましょう。
tanθ2=Xとおきます。
$$\frac{\frac{120}{119}-X}{1+X\frac{120}{119}}=1\Leftrightarrow\frac{120}{119}-X=1+X\frac{120}{119}$$
$$\Leftrightarrow X\frac{239}{119}=\frac{1}{119}\Leftrightarrow X=\frac{1}{239}$$
これを見ると、「239」という謎の半端な数字が120+119である事が分かります。以上から、結論が完全に分かっている前提での証明でしたが確かにマチンの公式が成立している事が分かります。
$$\frac{\frac{120}{119}-\frac{1}{239}}{1+\frac{1}{239}\frac{120}{119}}=\frac{28680-119}{28441+120}=\frac{28561}{28561}=1$$
$$よって、\tan\left(4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)\right)=1なので$$
$$4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)=\frac{\pi}{4}$$
Arctanxのマクローリン展開からマチンの公式の左辺を計算すると、
おおよそ4×0.1974-1/239≒0.785≒π/4となり、確かに公式の内容が成立している事を見れます。【Arctan(1/239)≒1/239としました。】
しかし上式を見れば分かるようにマチンの公式自体は近似式ではなく「等式」であり、しかも極限を含んでいない事が特徴です。
実は円周率を表す式としては「マチン型」というタイプのものが複数あって、比較的有名なものだとオイラーによるものとガウスによるものがあります。いずれもπ/4を逆正接関数の具体的な値の和や差で表す公式です。
例4:有理関数の積分に関する定理
これもまた数学の理論的な話ではありますが、間接的には応用にも関わる問題として
「有理関数(多項式の分数で表される関数)の一般的な積分は原始関数としてどのように表せるか」
というものがあります。
実はそれは初等関数のみで表す事ができ、しかも有理関数、対数関数、逆正接関数とそれらの合成関数さえあれば(理論上は)足りる」という結果を述べる定理があります。
意外かもしれませんが「逆正接関数Arctanx」が必要な関数として入っているわけです。
2つの多項式P(x)とQ(x)がある時、P(x)/Q(x)で表される有理関数の不定積分は理論上、次の関数によって表す事ができます。
- (別の)有理関数V(x)/W(x)
- 対数関数(底は e)
- 逆正接関数 Arctanx
- これら3つの合成関数
ここで「理論上」という語を付したのは「数学的に可能であるという事」と「それが便利であるか・使いやすいか」という事は別の問題である事も多いからです。
しかし理論上の話ではあっても、「原始関数を探す形で積分はどこまで計算できるのか?」という疑問に対して「三角関数の使用も含めて有理関数の範囲では、原始関数は初等関数の組み合わせで必ず導出する事が一応可能である」という一定の答えを述べている定理でもあります。
有理関数とは例えば次のようなものです。 $$\frac{P(x)}{Q(x)}=\frac{p_0+p_1x+p_2x^2+p_3x^3}{q_0+q_1x+q_2x^2+q_3x^3+q_4x^4}$$ $$具体例:\hspace{5pt}\frac{P(x)}{Q(x)}=\frac{2-x+3x^2+x^3}{1+x+2x^3-x^4}$$ 三角関数の有理関数の例 $$\frac{1-\tan^2x}{1+\tan^2 x}$$
定理の証明の概略を記すと、まず分子の次数のほうが分母よりも大きい場合には多項式の割り算をして、分母の次数のほうが大きい状態にします。
次に分母の多項式を因数分解して、そこから部分分数展開をする事を考えます。
「因数分解と言うができないような多項式だったらどうするのか」と思われるかもしれませんが、実は任意の多項式は何かしらの複素数(実数を含めて)を用いて理論上は因数分解できる事が知られています。それはいわゆる代数学の基本定理による帰結です。
計算をすると、任意の多項式は次の3つの項に分類して分ける事ができます。
- 分母が定数である(1を含めて)多項式
- 分母が1次式のベキ乗で分子は定数である項
- 分母が2次式のベキ乗で分子は1次式である項
因数分解をした時に実数以外の複素数が含まれている場合には共役を上手く使って虚数単位が式に現れないように工夫します。分母が2次式のベキ乗の項にはその意味があります。
さてその段階に至ると原始関数を探す形で積分ができます。この時に、使用する初等関数の種類は理論上3つであるという事が言えるのです。
- 単項式と多項式および有理関数:
分母に分母に定数以外が含まれない多項式および1/{(x-a)n}【n≧2】、
分母が2次の項に由来するx/{(x2+1)n}【n≧2】 - 対数関数:1/(x-a)および分母が2次の項に由来するx/(1+x2)の項
- 逆正接関数:2次の項に由来する1/(1+x2)の項
こうして見ると積分をする時に問題が生じるのが「分母の式」であって、1/(1+x2)の項を処理する時にどうしても必要なのが逆正接関数という事になります。
その項の不定積分は前述のように Arctanx+Cです。