三角関数の加法定理【証明】

三角関数の加法定理とは、三角関数の角度部分を和や差の形で表す時、個々の角度に対する三角関数の積と和などの組み合わせで計算できるという公式です。
（英：compound angle formulae）

高校数学の中では、その後に続く理論でも使うという意味では加法定理は重要な部類に入る関係式の１つであると言えます。

尚、対数関数についても「加法定理」という言葉を使用する事がありますが、ここでは三角関数についてのものを述べます。

定理の内容

■ 正弦と余弦の加法定理４式　■ 正接関数の加法定理

正弦と余弦の加法定理４式

三角関数の加法定理は、正弦・余弦・正接について存在しますが正弦と余弦の４式は次のようになります。

これら４式について、１つの符号を反転させればもう１つの式が得られるので
「実質は正弦と余弦について１つずつ」の２つであると見なすことも可能です。

これは、－Ｂ＝＋Ｂのように考えて式をまとめても支障はないという意味です。
sin(Ａ－Ｂ)＝sin(Ａ＋(－Ｂ))＝sinＡcos(－Ｂ)＋cosＡsin(－Ｂ)＝sinＡcosＢ－cosＡsinＢ
cos(Ａ－Ｂ)＝cos(Ａ＋(－Ｂ))＝cosＡcos(－Ｂ)－sinＡsin(－Ｂ)＝cosＡcosＢ＋sinＡsinＢ
のように導出はすぐにできるので、覚えるのは４式ではなく２式でも計算はできます。

４式でやるか２式でやるかは、理解しやすいほう・覚えやすいほうの考え方でよいと思います。
１つの角度の符号を反転させて別の式の導出をするという考え方は証明でも使います。
また、証明の時に最初に証明されるのはcos(Ａ－Ｂ)の式である都合上、最初から４式で考えたほうが理解しやすいという考え方もあります。

正接関数の加法定理

正接関数にも加法定理はありますが、正接は (正弦)／(余弦)で考えれば済む事と、使用頻度が比較的少ない事からここでは参考までに記しておきます。

これらの式は、正弦関数と余弦関数の加法定理が成立するという前提で示されます。

$$\tan (A+B)=\frac{\sin (A+B)}{\cos (A+B)}=\frac{\sin A \cos B +\cos A\sin B}{\cos A\cos B-\sin A \sin b}=\large{=\frac{\frac{\sin A}{\cos A}+\frac{\sin B}{\cos B}}{1-\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}}}$$
$$\tan (A-B)=\frac{\sin (A-B)}{\cos (A-B)}=\frac{\sin A \cos B -\cos A\sin B}{\cos A\cos B+\sin A \sin b}=\large{=\frac{\frac{\sin A}{\cos A}-\frac{\sin B}{\cos B}}{1+\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}}}$$

このようになる事が根拠であり、
後者の式は tan(－θ)＝tanθの関係を前者の式の結果に代入する事でも得られます。

証明

■ 考え方：三角比の範囲の場合
■ 一般角の場合①　余弦 cos (Ａ－Ｂ)の式の証明
■ 一般角の場合②　残り３式の導出　

考え方：三角比の範囲の場合

証明はいきなり一般の角度の場合でもできるのですが、まず図形上の考え方を見るために０°～９０°の範囲における三角比の中で加法定理が成立する事の説明をしましょう。

図のように単位円の「第１象限」の部分で２つの角度の考えて三角形を作ります。
ここで、２つの角度の差を考えます。図で言うと\(\alpha－\beta\) です。
具体的な角度を入れるなら、例えば６０°－１５°＝４５°などを考えています。

その差をとった角度の正弦や余弦をどのように考えるのかというと、図のように点Ａから点Ｂまでの距離をもとの正弦と余弦で表し、さらに△ＡＯＢに余弦定理を使用するのです。この時、線分ＡＢの距離は三平方の定理で計算できます。

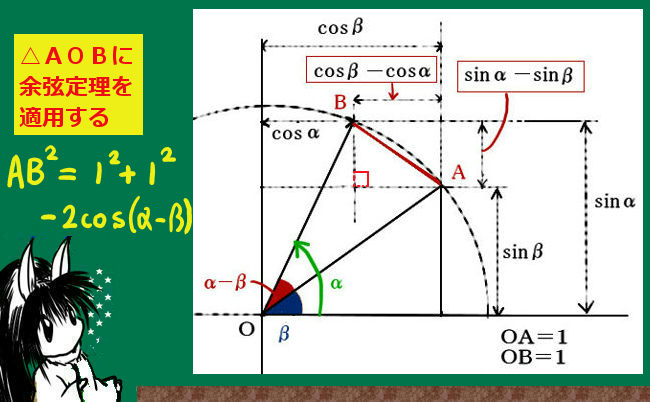
余弦定理で組み立てた式に三角比の公式 sin^２θ＋cos^２θ＝１ を適用すると、余弦に関する加法定理の関係式cos(Ａ－Ｂ)＝cosＡcosＢ－sinＡsinＢが得られるのです。

これはとりあえず０°～９０°の範囲の図形的な位置関係から関係式を導出するものですが、じつは三角関数として実数全体の範囲で一般の角度を考える場合でも、基本的な考え方は同じなのです。

• ２つの角度の２つの三角形を作り、その角度の差によりもう１つの三角形を考える。
• 三角形は、単位円周上の２点と原点で構成する。
• 円周上の２点間の距離を三平方の定理で表し、さらに余弦定理を適用する。

この基本的な考え方のもとで証明をしていきます。
尚、その場合だと得られるのは余弦の「差」に関するcos (Ａ－Ｂ)の式になりますが、その式が証明されると変数の置き換えで残り３式も証明されるという形になります。

一般角の場合①　余弦 cos (Ａ－Ｂ)の式の証明

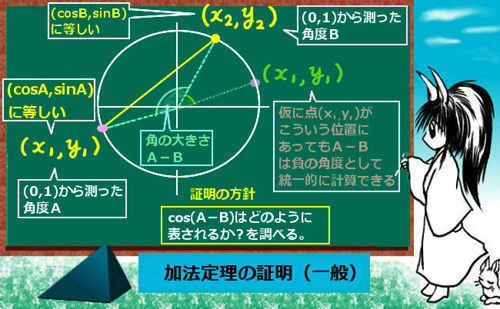
実数全体を範囲とする拡張された角度（一般角）でも加法定理が成立する事の証明は、一般的には次のように座標上の単位円周上の２点を考えて角度を統一的に扱います。

考え方自体は三角比の範囲の時と同じで、２点の「長さ」（プラスの値）を上手に使うのです。

まず単位円周上の２点（ｘ_１,ｙ_１）と（ｘ_２,ｙ_２）を考え、
これらの座標を（cosＡ,sinＡ）および（cosＢ,sinＢ）とおいてもよい事から始めます。
つまり(１,０)から２点まで測った角度をそれぞれＡおよびＢとしています。

このときの２点の位置関係は、ｘ座標で言うとどちらがどちらよりも大きくても（あるいは等しくても）構わず、むしろどちらの場合でも統一的に扱って証明の計算を進められる事がポイントです。

つまり、鋭角の場合・鈍角の場合・負の角度の場合・・といった場合分けをしなくてもよいという事です。

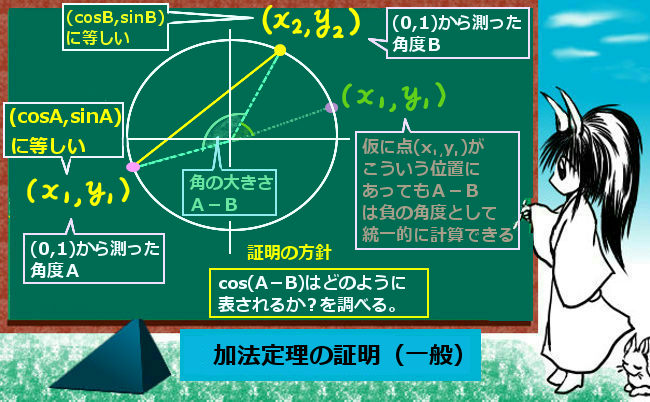
余弦の場合は、負の角度を代入しても同じ絶対値の正の角度を代入した時と同じ値である事【cos(－θ)＝cosθ】もポイントです。結論を言うと、加法定理のうち余弦の cos(Ａ－Ｂ)に着目するととうまくいくのです。

単位円周上の２点と原点で作られる三角形に注目します。この時に原点を頂点とする部分の角度はＡ－Ｂになります。（これは円周上の２点の位置関係によってプラスの値にもマイナスの値にもなります。）

この三角形に、余弦定理を適用します。余弦定理は辺の長さと１つの余弦に関して、実数全体の範囲の角度で正しい関係式を作ります。

２点の長さの出し方は三角比の範囲の時と同じで三平方の定理を使います。（座標上の２点の距離の一般的な計算方法でもあります。）余弦定理で必要なのは２乗の形なので、長さを２乗した形は次のようになります。

(cosＡ－cosＢ)^２＋(sinＡ－sinＢ)^２
＝cos^２Ａ＋cos^２Ｂ－２cosＡcosＢ＋sin^２Ａ＋sin^２Ｂ－２sinＡsinＢ
＝２－２cosＡcosＢ－２sinＡsinＢ

【cos^２Ａ＋sin^２Ａ＝１、cos^２Ｂ＋sin^２Ｂ＝１なのでこのように式が簡単になります。】

他方、三角形の残りの２辺は単位円の半径ですから長さはともに１です。この条件のもとで余弦定理を考えてみると次のようになります。

(cosＡ－cosＢ)^２＋(sinＡ－sinＢ)^２＝１^２＋１^２－２・１・１・cos(Ａ－Ｂ)
⇔２－２cosＡcosＢ－２sinＡsinＢ＝１＋１－２cos(Ａ－Ｂ)
⇔ cos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢ

【最後の式変形は両辺にある定数の「２」を消し、さらに両辺をー２で割り整理したものです。】

このように、加法定理のうち余弦の「差の形」のものが成立する事が分かります。この形は２乗の展開式に由来するものというわけです。また、角度の差をとる時に２つの項がプラスで結ばれる理由も証明の過程から比較的明確であるかと思います。２点間の距離の計算による２乗の展開式由来なので同符号というわけです。

この場合の角度には、三角関数の変数としての実数全体の範囲の任意の角度を代入しても成立します。これは余弦定理が実数全体の範囲で角度を代入した場合にも正しい関係式を作っているためです。円周上の２点と原点が同一直線上に並んで「三角形を作らない」場合にでも点同士の距離と余弦関数の値の正しい関係を表しています。

一般角の場合②　残り３式の導出

正弦と余弦に関する加法定理の残り３式はどのように導出するのかというと、それらはcos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢをもとに出すのです。

まず、Ｂがプラスでマイナスであってもこの関係式は成立しますから、Ｂの部分を－Ｂに置き換えるとcos(Ａ＋Ｂ)＝cosＡcos(－Ｂ)＋sinＡsin(－Ｂ)＝cosＡcosＢ－sinＡsinＢとなります。

正弦のほうはどうするのかというと、ＢをＢ＋\(\pi\)／２に置き換えます。

cos(Ａ＋Ｂ＋\(\pi\)／２)＝cosＡcos(Ｂ＋\(\pi\)／２)－sinＡsin(Ｂ＋\(\pi\)／２)＝－cosＡsinＢ－sinＡcosＢ

他方で cos(Ａ＋Ｂ＋\(\pi\)／２)＝－sin(Ａ＋Ｂ) でもあるので、

－sin(Ａ＋Ｂ)＝－cosＡsinＢ－sinＡcosＢ⇔sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ

正弦の残り１式は、sin(Ａ＋Ｂ) のＢを－Ｂに置き換えて得ます。sin(Ａ＋Ｂ)＝sinＡcos(－Ｂ)＋cosＡsin(－Ｂ)＝sinＡcosＢ－cosＡsinＢ です。

これによって、正弦関数と余弦関数の加法定理４式が確かに成立する事になります。

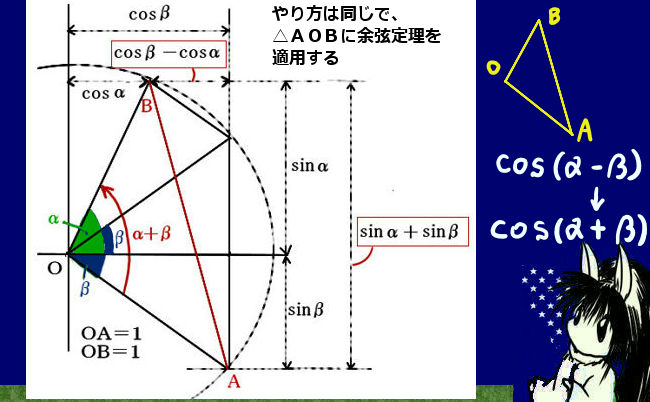
参考までに、三角比の範囲の場合に cos(Ａ－Ｂ)のＢを－Ｂに置き換えてcos (Ａ＋Ｂ)にした場合の図形的意味は次図のようになります。これを一般化しているのが、三角関数で考えた一般の角度での加法定理です。単位円周上で考えれば、同様の図形的な位置関係を必ず作る事ができます。

具体例・応用例・覚え方

具体例についても見てみましょう。

例えば、９０°＝６０°＋３０°、９０°＝４５°＋４５°といった関係を加法定理は正しく表すでしょうか？

$$\sin\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{6}\right)+\cos\left(\frac{\pi}{3}\right)\sin\left(\frac{\pi}{6}\right)$$

$$=\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{1}{2}\cdot\frac{1}{2}=\frac{3}{4}+\frac{1}{4}=1$$

$$\sin\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{2}\right)=1 で一致します。$$

４５°のほうでやってみても同じで、

$$\sin\left(\frac{\pi}{4}+\frac{\pi}{4}\right)=\sin\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{4}\right)\sin\left(\frac{\pi}{4}\right)$$

$$=\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}=\frac{1}{2}+\frac{1}{2}=1$$

こういう形で成立するわけです。

１２０°－６０°＝６０°の場合を今度は余弦のほうでやってみると、

$$\cos\left(\frac{2\pi}{3}-\frac{\pi}{3}\right)=\cos\left(\frac{2\pi}{3}\right)\cos\left(\frac{\pi}{3}\right)+\sin\left(\frac{2\pi}{3}\right)\sin\left(\frac{\pi}{3}\right)$$

$$=-\frac{1}{2}\cdot \frac{1}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}=-\frac{1}{4}+\frac{3}{4}=\frac{1}{2}=\cos\left(\frac{\pi}{3}\right)$$

加法定理が成立するなら、既知の三角関数の値を使って例えば４５°－３０°＝１５°といった半端な角度の正弦や余弦の値も分かるはずです。「１５°」における正弦の値を加法定理で計算すると次のようになります。

$$\sin\left(\frac{\pi}{12}\right)=\sin\left(\frac{\pi}{4}-\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{6}\right)-\cos\left(\frac{\pi}{4}\right)\sin\left(\frac{\pi}{6}\right)$$

$$=\frac{1}{\sqrt{2}}\cdot\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\cdot\frac{1}{2}=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4}$$

この計算値は約 0.2588 で、マクローリン展開で計算した値にほぼ一致します。

４５°＋４５°や６０°＋６０°のような場合は、より一般的にＡに対する２Ａとして「倍角の公式」の形にして捉える事も可能です。和積の公式や積和の公式も、加法定理の幾つかの式を組み合わせて変形したものです。

三角関数の微分公式の証明でも、加法定理を使用して計算を進めます。

加法定理の式の形の「覚え方」としては、複素数を利用する方法もあります。【これらは「説明」や「覚え方」としては有用ですが「証明」にはならないので注意。】

複素数の場合、指数関数表示（オイラーの公式）からｅ^ｉ(θ＋φ)＝ｅ^ｉθｅ^ｉφですが、
cos(θ＋φ)＋ｉsin(θ＋φ)＝(cosθ＋ｉsinθ)(cosφ＋ｉsinφ)
＝cosθcosφ－sinθsinφ＋ｉ(sinθcosφ＋cosθsinφ)
を意味しますから、実部と虚部の値を比較すれば
cos(θ＋φ)＝cosθcosφ－sinθsinφ、sin(θ＋φ)＝sinθcosφ＋cosθsinφ
の関係が成立している事が分かります。
これらは三角関数の加法定理の内容そのものです。

（これはド・モアブルの定理で考えても同じです。
ただし、その定理の証明に加法定理が使用されているので、「加法定理の証明」としては
適切とは言えないのです。）

外積を使った証明

加法定理の別の証明方法として、３次元ベクトルの外積（ベクトル積、クロス積）を使う方法があります。

外積ベクトルは３次元のベクトルに対して考えるものですが、ｚ＝０としたｘｙ平面上の２つのベクトルに対して考える事は一応可能です。

そこで、次の２つのベクトルを考えます。
（角度θとφはプラスの値とします。ベクトルの大きさはどちらも１である事にも注意。）

$$\overrightarrow{a}=\cos\theta\hspace{2pt}\overrightarrow{e_1}+\sin\theta\hspace{2pt}\overrightarrow{e_2},\hspace{10pt}\overrightarrow{b}=\cos\phi\hspace{2pt}\overrightarrow{e_1}-\sin\phi\hspace{2pt}\overrightarrow{e_2}$$

$$\overrightarrow{e_1}=(1,0,0),\hspace{10pt}\overrightarrow{e_2}=(0,1,0),\hspace{10pt}（本当は\overrightarrow{e_3}=(0,0,1)もある。）$$

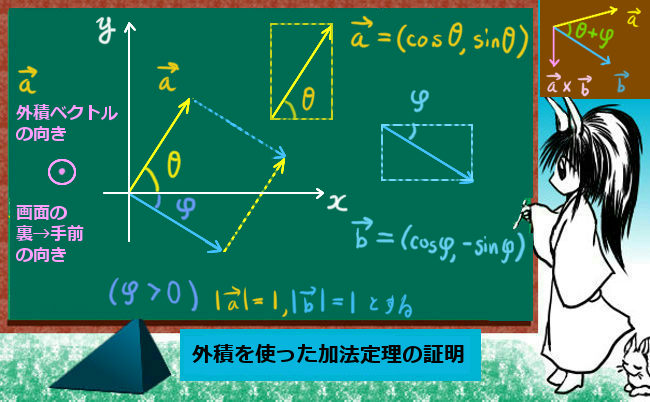
そこで外積ベクトルを考えてみましょう。（外積について成立する公式を使用します。）

$$\overrightarrow{a}×\overrightarrow{b}=(\cos\theta\hspace{2pt}\overrightarrow{e_1}+\sin\theta\hspace{2pt}\overrightarrow{e_2})×(\cos\phi\hspace{2pt}\overrightarrow{e_1}-\sin\phi\hspace{2pt}\overrightarrow{e_2})$$

$$=-\cos\theta\sin\phi(\overrightarrow{e_1}×\overrightarrow{e_2})+\sin\theta\cos\phi(\overrightarrow{e_2}×\overrightarrow{e_1})$$

$$=-\cos\theta\sin\phi(\overrightarrow{e_1}×\overrightarrow{e_2})-\sin\theta\cos\phi(\overrightarrow{e_1}×\overrightarrow{e_2})$$

$$=-(\cos\theta\sin\phi+\sin\theta\cos\phi)(\overrightarrow{e_1}×\overrightarrow{e_2})$$

$$=(\cos\theta\sin\phi+\sin\theta\cos\phi)(-\overrightarrow{e_3})$$

他方で、この外積ベクトルは定義通りに考えれば向きは「ｚ軸のマイナス方向」であり、
大きさは\(|\overrightarrow{a}||\overrightarrow{b}|\sin(\theta+\phi)=\sin(\theta+\phi)\) です。

という事は、

$$\overrightarrow{a}×\overrightarrow{b}=\sin(\theta+\phi)\hspace{2pt}(-\overrightarrow{e_3})$$

という事でもありますから、２つの結果を等号で結べます。

$$(\cos\theta\sin\phi+\sin\theta\cos\phi)(-\overrightarrow{e_3})=\sin(\theta+\phi)(-\overrightarrow{e_3})$$

$$よって、\sin\theta\cos\phi+\cos\theta\sin\phi=\sin(\theta+\phi)【加法定理の証明終り】$$

この場合は、正弦の加法定理が直接示されています。（証明の最後の箇所では見やすいように項の順番だけ入れ替えています。）これを使って残りの３式も証明が可能です。

ここで行った計算は一体何なのかというと、前半で記した証明が三角形の「辺の長さ」を考えたのに対して、この外積を使った証明では平行四辺形の「面積」（三角形でも可能）を使ったという事です。本質的には、座標を使って証明するという同じ部類の２つの証明法と言えます。