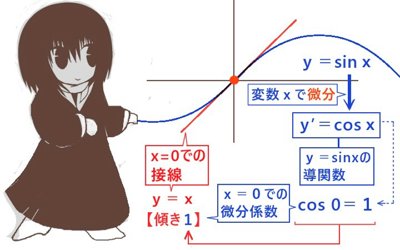
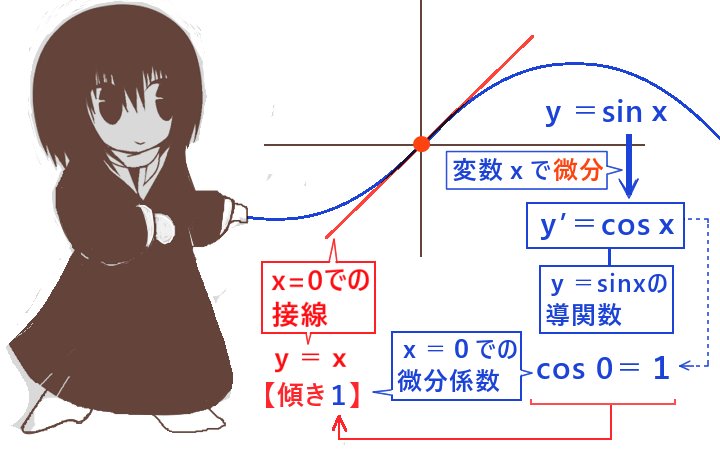
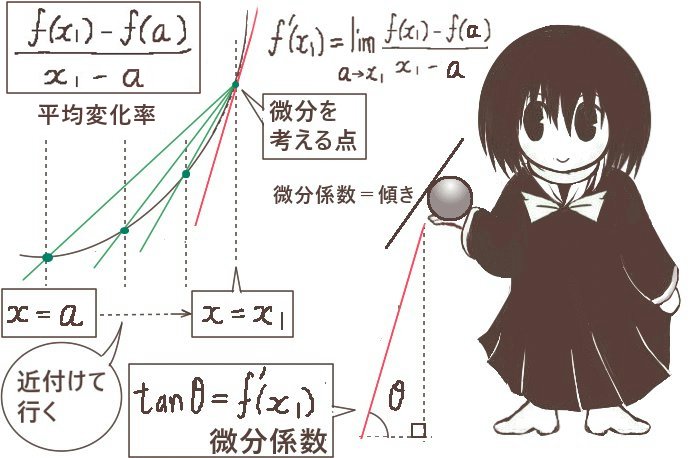
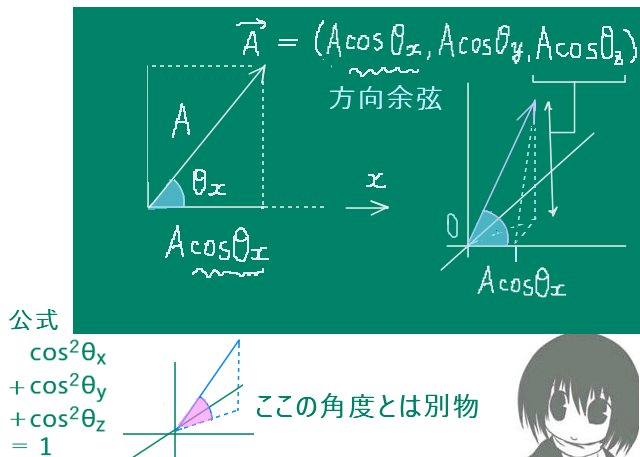
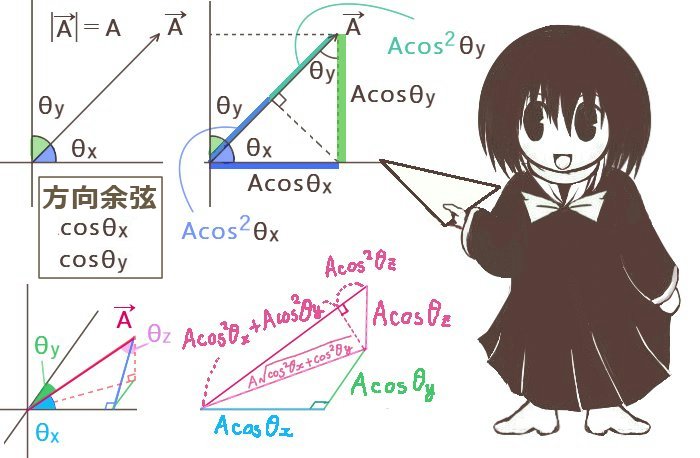
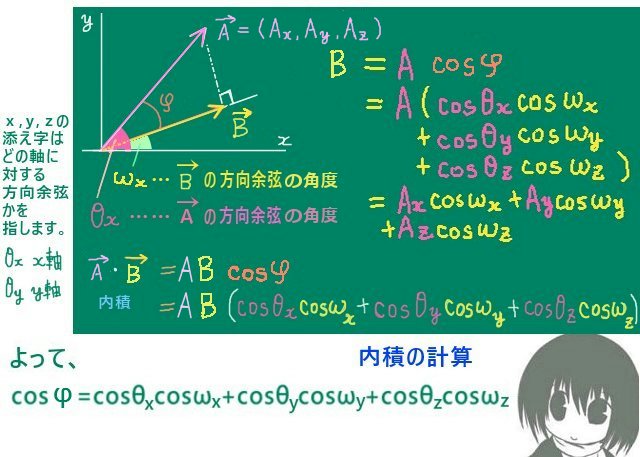
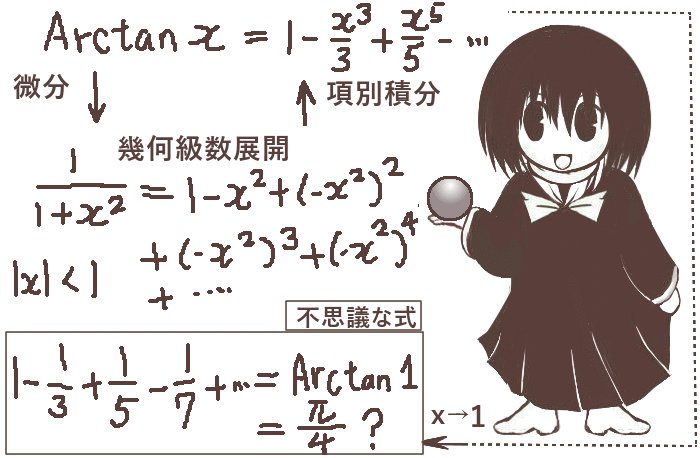
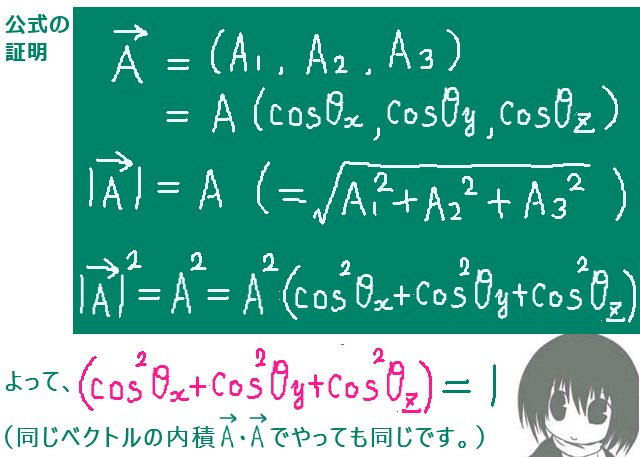ライプニッツ級数とは「分子が1で分母を奇数とする分数を、プラスマイナスの符号を交互に変えて加えて行くと円周率の1/4に収束する」という無限級数を指します。
この無限級数の導出方法はいくつか存在し、ここでは図形的な考察をもとにした式変形と定積分の計算、それと幾何級数展開を使った導出方法を説明します。
ライプニッツ級数の導出方法はここで説明するものだけではなく、いくつか方法があります。例えば、逆正接関数のマクローリン展開から導出する方法や、連分数展開によって得る方法などがあります。
数学史的には、π/4=1ー1/3+1/5-1/7+・・・という式自体はライプニッツ以外の学者によっても独立に得られていた事が知られています。
また、この記事内でも後述しますが
「ライプニッツ級数1ー1/3+1/5-1/7+・・・がπ/4という値に収束する事」と
「ライプニッツ級数が収束するか否かの判定」は、実は別々に考察できます。
ライプニッツ級数は交代級数(交項級数)という種類の無限級数の1つです。
備考として、一般の交代級数が収束する十分条件を提示する命題は「ライプニッツの定理」と呼ばれる事があります。
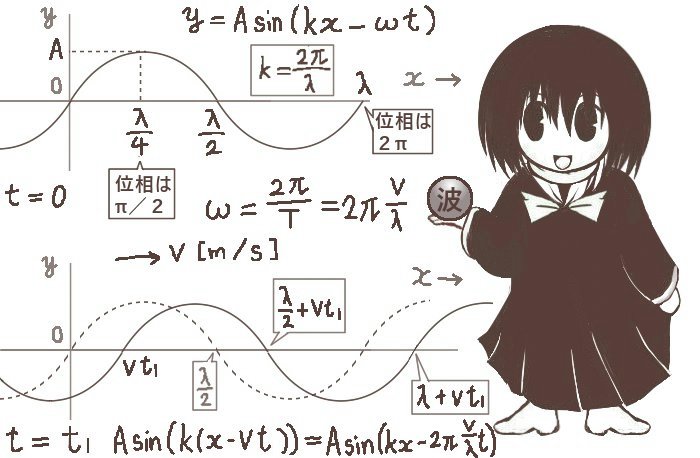
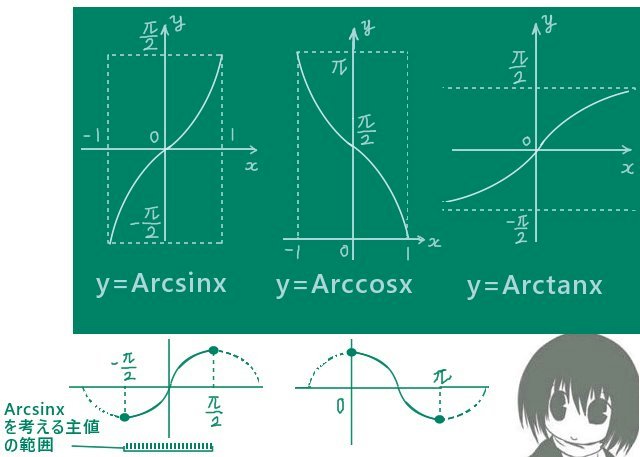
ライプニッツ級数とは
まず、ライプニッツ級数の具体的な表式は次のようになります。
次の式で表される無限級数がライプニッツ級数です。\(\pi\) は円周率です。 $$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+\cdots$$ $$\left(≒0.785398\cdots\right)$$ この値は無理数になります。
無理数を「有理数で表せる」?
ライプニッツ級数の左辺は無理数ですが右辺は「各項が有理数である無限級数」となっています。
これについては、右辺が表す無限級数は「π/4という無理数に収束するという事」すなわち 「項数を増やせばπ/4という無理数との差をいくらでも小さくできる事」を意味しています。
ですので、ライプニッツ級数の式において「無理数≠有理数」という当然の関係式は崩れてはいません。どこか有限の項数で計算をやめたら、 その値はπ/4には一致しない事になります。しかし項数を増やせばπ/4との差はいくらでも縮まります。それが、ライプニッツ級数が数式的に表すものです。
ライプニッツ級数は特徴的な式の形をしているため、「奇数だけを用いて円周率を表せる」というキャッチ―な表現が使われる事があります。 その表現自体は誤っているわけではありませんが、「無限級数が収束する値として円周率を表せる」という事を踏まえておく必要があります。
ライプニッツ級数が「無限級数」でありπ/4が「極限値」である事を、より明確に表すのであれば次のようになります。
$$\frac{\pi}{4}=\lim_{n \to \infty}\sum_{k=0}^n\frac{(-1)^k}{2k+1}=\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}$$
但し、多くの場合はライプニッツ級数は「円周率と奇数」の関係を強調して
1-1/3+1/5-・・・の形で書かれます。
3.141592・・・をライプニッツ級数で出せる?
円周率の 3.141592・・・の値を計算する式としては、実はライプニッツ級数はあまり優れた式ではありません。無限級数の収束の速さが遅く、 項数を非常に多く増やさないと3.14・・・の値に近付いて行かないためです。(円周率の数値計算用として優れた式としては、 複数のマチン型の公式が知られています。逆三角関数の記事で解説。) 変更なし:
もし整数だけを準備して円周率計算が手計算で簡単にできるなら何とも便利そうですが、 式として興味深い形をしている事と色々な意味での実用性や有用性は残念な事に必ずしも重ならないという例になっています。
「奇数」が得られる根拠
ライプニッツ級数において、「奇数」以前に「整数」が得られるのはなぜでしょう。それは具体的には、単項式の微分法を根拠にしています。
x3の微分(「導関数」)は3x2になります。積分を行う場合は逆の演算です。
x2の原始関数はx3/3です。
この関係によって1/3,1/5,1/7といった「分母が整数である分数」が式中に発生します。
ライプニッツ級数に限らず、計算式中の「整数」の出所が微分法や積分法であるという場合は少なからずあります。
次に、ライプニッツ級数の各項において「偶数が欠けている」理由は幾何級数展開(等比級数展開)を使う時の公比の形に由来しています。
具体的には、-z2という公比による幾何級数展開を考えて1ーz2+z4-z6+・・・という式を得て、 さらにそれにz2を乗じてz2ーz4+z6-z8+・・・の形を作ります。 そして、その各項を積分(項別積分)する事でz3/3ーz5/5+z7/7-z9/9+・・・の形の式を得ます。 これがライプニッツ級数の形を作っているわけです。無限級数の項別積分を実行可能であるには条件がありますが、ここではそれを満たします。
具体的には、-z2という公比による幾何級数展開を考えて1ーz2+z4-z6+・・・という式を得て、 さらにそれにz2を乗じてz2ーz4+z6-z8+・・・の形を作ります。 そして、その各項を積分(項別積分)する事でz3/3ーz5/5+z7/7-z9/9+・・・の形の式を得ます。 これがライプニッツ級数の形を作っているわけです。無限級数の項別積分を実行可能であるには条件がありますが、ここではそれを満たします。
ライプニッツ級数において幾何級数展開が使われる部分は正確には「1/3」以降の項からであり、最初の「1」は出所が異なる事になります。
幾何級数展開の式を使用する事は「無限級数が得られる事」と「プラスとマイナスが交互に出てくる事」の根拠でもあります。 そのため、次に述べて行くライプニッツ級数の導出方法では微積分の基本計算と並んで幾何級数展開が非常に重要な要素となっています。但し、 この幾何級数展開を使用するには「公比の絶対値が1未満である」という条件があるので注意が必要です。
- 円とその接線の式、面積の関係などから得る式変形と変数変換(円周率は円の面積から)
- 単項式(x2など)の積分計算(「奇数」が分母にある根拠)
- 幾何級数展開(無限級数の形となる根拠)

証明と導出【四分円の面積を利用する方法】
全体の流れ
大きく分けて記すと次のようになります。
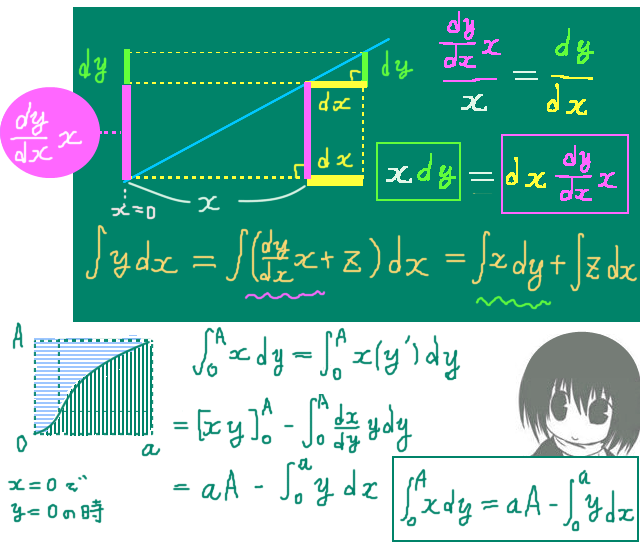
$$四分円y=\sqrt{2x-x^2}に対してy=\frac{dy}{dx}x+zという式変形を考えるとx=\frac{2z^2}{1+z^2}$$
$$|z|<1のもとで幾何級数展開により\frac{1}{1+z^2}=1-z^2+z^4-z^6+\cdots$$
$$部分積分と置換積分により\int \left(\frac{dy}{dx}x+z\right) dx=\frac{1}{2}\left(xy+zx-\int x dz\right)と変形できる。$$
その後、幾何級数展開した箇所について項別積分を行い積分区間の端点の極限を考慮したうえで計算を進め、 得られる無限級数の収束値が半径1の四分円の面積π/4に等しいという形でライプニッツ級数を導出できます。
$$\lim_{\epsilon \to 0, \delta \to 1}\int_\epsilon^\delta y dx=1-\lim_{\epsilon \to 0, \delta \to 1} \left[\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right]_\epsilon^\delta$$
$$=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$
$$これが半径1の四分円の面積\int _0^1y dx=\frac{\pi}{4}に等しい。$$
以下、各過程を詳しく見て行きます。
①円の式と導関数
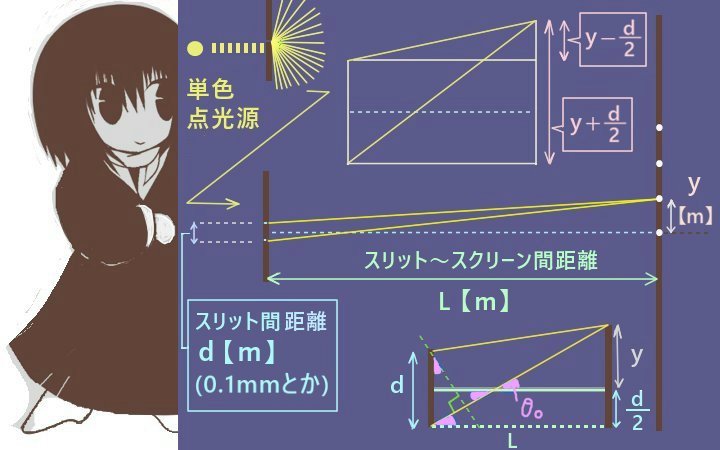
具体的な計算としては半径が1の四分円(半円のさらに半分)の面積を定積分で計算します。
しかし円を表す式を使って普通に定積分の計算をする
(置換積分か逆三角関数を使用)と、π/4という値は出ますが1-1/3+1/5-・・・という無限級数の式は出てきません。
閉区間 [0, 1] およびy≧0の範囲における、中心座標(1,0)半径1の円の式を使います。 $$y^2 +(x-1)^2=1\hspace{3pt}$$ $$\Leftrightarrow y^2 +x^2 -2x=0$$ $$y≧0においては、y=\sqrt{2x-x^2}$$ $$y>0の時、\frac{dy}{dx}=\frac{1-x}{\sqrt{2x-x^2}}\left(=\frac{1-x}{y}\right)$$ 微分により得られる導関数dy/dxはこの後で積分計算に使用しますが、x=0の時に無限大になってしまう (図形的に接線はx軸に垂直でy軸に平行となる)ので、厳密にはx=0は積分区間に含める事ができず極限値を考える必要があります。導関数を考えないなら普通に原点を積分区間に含める事ができます。
微分の計算は次のようにしています。合成関数の微分法を使います。(ここでの場合は、後述する図形的考察でもこの導関数は導出可能です。)
$$\frac{dy}{dx}=\frac{d}{dx}\sqrt{2x-x^2}=\frac{d}{dx}\left(2x-x^2\right)^{\frac{1}{2}}=\frac{1}{2}\left(2x-x^2\right)^{-\frac{1}{2}}\cdot (2-2x)=\frac{1-x}{\sqrt{2x-x^2}}$$
半径1の円の面積は1×1×π=πです。その1/4である四分円の面積はπ/4です。この値が無限級数1ー1/3+1/5-1/7+・・・の収束値である事を積分を使って証明して行きます。
しかしy≧0における円の式をそのままxで定積分するとπ/4の値は得られますが無限級数の式は得られません。何か別の方法で円の面積を計算する必要があります。

②円の接線の式を利用して関係式を作る
そこで、実は「円の接線の式」を利用すると通常とは異なる形で面積の積分計算ができます。
但し積分を行う対象の関数は円の式なので、接線上の点を考えるわけではなく「円周上の点(x,y)に対して成立する関係式」を接線の式を利用して作ります。
円周上の点(x,y)における接線の傾きはdy/dxで表される導関数です。そして、接線のy切片(接線とy軸の交点)をzとします。この時にy=(dy/dx)x+zが成立します。
この時にzはxの関数です。そのようなz=z(x)という関数がxの開区間(1,0)の範囲内において円周上の点(x,y)に対して必ず存在できます。 このzの値が存在できる事は図形的に見ても確認できますが、式でも確かに示せます。
$$y>0においてy=\frac{dy}{dx}x+zとすると、\frac{dy}{dx}=\frac{1-x}{y}であるので$$
$$y=\frac{x-x^2}{y}+z\Leftrightarrow zy=y^2-(x-x^2)=y^2-x+x^2$$
$$円の式y^2 +x^2 -2x=0より、zy=x$$
$$y>0であればz=\frac{x}{y}=\frac{x}{\sqrt{2x-x^2}}$$
ここで考えているy=(dy/dx)x+zという式は、 あくまで円周上の点(x,y)に対して成立する式です。接線自体の式として考える場合はxとyを接線上の点の座標として考えるわけですから、円周上の点を別の文字で例えば(a,b)として表し、 その点における微分係数f’(a)を使う必要があります。その時に接線の式はy=f’(a)x+z(a)であり、これは接線上の点(x,y)に対して成立する関係式です。
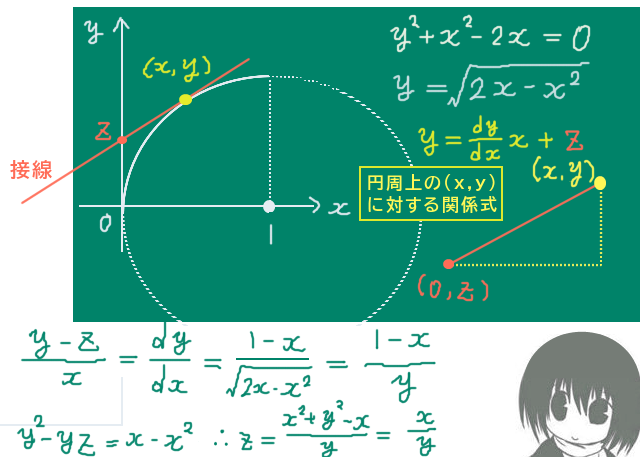
この時にxをzで表す事もでき、後の計算で重要です。
$$z=\frac{x}{\sqrt{2x-x^2}}=\sqrt{\frac{x}{2-x}}から、z^2(2-x)=x$$
$$\Leftrightarrow x=\frac{2z^2}{1+z^2}$$
この後の計算では、このzを変数として四分円の面積を積分計算する事を考えて行きます。xをzで表した式を見ると分母が1+z2となっており、これが幾何級数展開可能な式の形になっています。
0<z<1の範囲においてはzで表したxの式は、公比を-z2とした幾何級数展開が可能です。 $$x=\frac{2z^2}{1+z^2}=2z^2(1-z^2+z^4-z^6+\cdots)$$
(補足)図形的にy切片と導関数を計算する場合
上記の計算でzの具体的な形としてz=x/yが得られましたが、この関係は平面幾何的にも導出できます。ここで考えている円はy軸が原点における接線となっているので、「接線のy切片と接点と円の中心」で作られる三角形を考えて合同関係に着目すれば三平方の定理によってzとxおよびyとの関係式を作る事ができます。
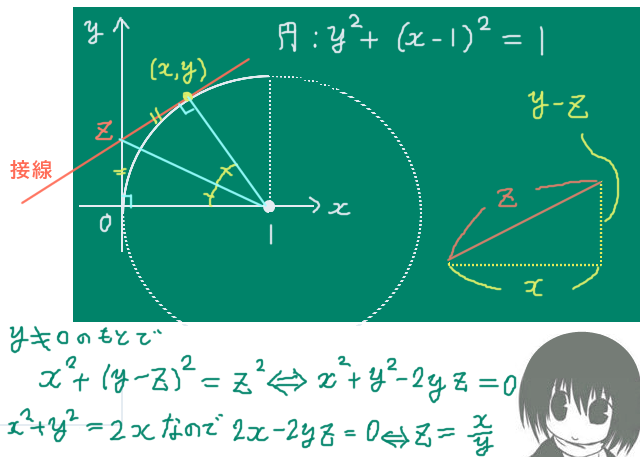
同じく図形的考察からy>0において接線の傾きは(yーz)/x=(y2ーx)/(xy)です。そしてyをxで表すと、微分により得る導関数と同じ式を得ます。
$$y>0の時、接線の傾きは\frac{y-z}{x}=\frac{y-\frac{x}{y}}{x}=\frac{y^2-x}{xy}$$
$$=\frac{2x-x^2-x}{x\sqrt{2x-x^2}}=\frac{x-x^2}{x\sqrt{2x-x^2}}=\frac{1-x}{\sqrt{2x-x^2}}\left(=\frac{dy}{dx}\right)$$
③積分においてyの形を変形する(面積変換定理)
次に四分円の面積を積分によって考えます。この時に、積分変数xでyを積分する計算において
y=(dy/dx)x+zの式変形をしてzを積分計算に持ち込みます。以下、まず積分区間に依存せずに不定積分で可能なところまで式変形の計算を進めて行きます。
$$\int ydx=\int\left(\frac{dy}{dx}x+z\right)dx$$
この段階では積分変数の変換を行ったわけではありません。
(dy/dx)x+z={(1-x)/y}・x+x/y
=(2x-x2)/y
=y2/y=y
という関係を使ってyを表しているだけとなります。
次に2つの項のそれぞれについて積分変数の変換を考えます。
まず(dy/dx)xの項については部分積分の公式を適用して変形をします。
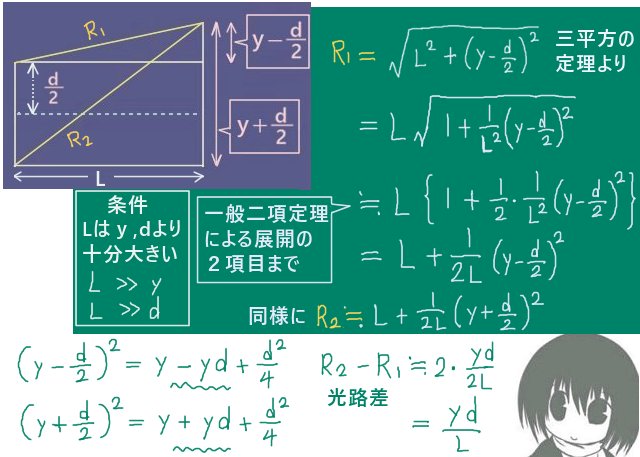
$$\int\frac{dy}{dx}xdx=xy-\int y\left(\frac{d}{dx}x\right)dx=xy-\int ydx$$
この部分積分による式変形は、定積分で計算した時には長方形領域の面積を曲線で分割した時の関係を表す意味を持ちます。
置換積分を行ってから(d/dy)y=1が乗じられていると見て部分積分を行い、積分の項に対して再度置換積分を行って積分変数をxに戻す事でも同じ式を得ます。$$最初に置換積分を行うと、\int\frac{dy}{dx}xdx=\int xdy$$ $$次に積分変数yで部分積分を行うと\int x dy=\int x \left(\frac{d}{dy}y\right)dy=xy-\int\frac{dx}{dy}ydy$$ $$置換積分を再度適用してxy-\int\frac{dx}{dy}ydy=xy-\int y dx$$ 但し、定積分を行う時にはxでの積分であったかyでの積分であったか注意も必要です。(ここでの四分円に対する計算ではx=0の時y=0でx=1の時y=1なので結果的にそれほど問題は起こらない。)
同様の部分積分の適用の仕方でzの項についても式変形し、
さらに置換積分によって「積分変数zでxを積分する」形に変形します。
$$\int z dx=\int z \left(\frac{d}{dx}x\right)dx=zx-\int\frac{dz}{dx}xdx=zx-\int x dz$$
置換積分と部分積分の順序を入れ換えて、置換積分を先に実行して積分変数をxからzに変える 事もできます。定積分する時には積分変数に注意。 $$単純に置換積分を行った場合は、\int zdx=\int z\frac{dx}{dz}dz$$ $$=zx-\int\left(\frac{d}{dz}z\right)xdz=zx-\int xdz$$
式を整理すると、積分変数xによるyの積分の項が2つあるのでまとめる事ができます。
$$\int y dx=xy-\int y dx+zx-\int x dz$$
$$\Leftrightarrow 2\int y dx=xy+zx-\int x dz$$
$$\Leftrightarrow \int y dx=\frac{1}{2}\left(xy+zx-\int x dz\right)$$
ここで式中のxyととzxは積分変数をxとして考えた時の原始関数です。但し上記の補足説明のように積分変数をyやzで計算した場合はyやzの原始関数として端点の値を代入する必要があります。
$$\int y dx=\frac{1}{2}\left(xy+zx-\int x dz\right)$$この関係式を定積分で考えたもの(あるいはzに関する計算をする前の段階のもの)はライプニッツの面積変換定理と呼ばれる事があり、円の式に限らず積分可能な一般の1変数関数に対して成立します。図形的な意味としては積分における面積計算の領域を2つに分けて、そのうちの1つを接線のy切片であるzによって積分計算しているものになります。
尚、この式の右辺をxで微分するとyに等しくなる「はず」ですが、
具体的にチェックをしてみると次のようになります。
$$zはxだけの関数で表せる事と、\int x dz=\int x\frac{dz}{dx}dxに注意して、$$
$$\frac{d}{dx}\frac{1}{2}\left(xy+zx-\int x dz\right)=\frac{1}{2}\left(y+x\frac{dy}{dx}+z+x\frac{dz}{dx}-x\frac{dz}{dx}\right)$$
$$=\frac{1}{2}\left(y+x\frac{dy}{dx}+z\right)=\frac{1}{2}\left(y+y\right)=y$$
④幾何級数展開を適用
「xを積分変数zで積分する」項について、0<x<1の時に0<z<1であるので1/(1+z2)の部分に対して幾何級数展開を適用できます。公比は-z2です。
$$\int y dx=\frac{1}{2}\left(xy+zx-\int x dz\right)において、$$
$$\int x dz=\int \frac{2z^2}{1+z^2}dz=2\int z^2\cdot\frac{1}{1+z^2}dz$$
$$=2\int z^2(1-z^2+z^4-z^6+\cdots)dz=2\int(z^2-z^4+z^6-z^8+\cdots)dz$$
$$=2\left(\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right)$$
これを項別積分するには関数列が一様収束するという条件が必要ですが、ここではその条件は満たされています。(収束する整級数が一様収束する事の証明は、連続性定理の証明の一部として後述。級数変化法による計算と、コーシー列に関する考察を含みます。)
よって、次式が成立します。
$$\int y dx=\frac{1}{2}\left(xy+zx-\int x dz\right)=\frac{1}{2}\left(xy+zx\right)-\left(\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right)+C$$
(この段階ではまだ不定積分で考えているので、積分定数Cを加えた形にしています。)
ここで行われた式変形を細かく表現すると
「0<x<1の範囲内で0<z<1であり、
その範囲の任意のzに対して公比を-z2として1/(1+z2)を幾何級数展開できる」
という事になります。
幾何級数(等比級数)は公比の絶対値が1未満である時は公式を適用できます。
$$|r|<1の時、1+r+r^2+r^3+\cdots=\frac{1}{1-r}$$
(導出:第n項までの和をSとして、S-rS=(1-r)Sを計算して(1-r)で割り、n→∞)
逆に、|r|<1の時に1/(1ーr)の形の項は幾何級数の形に展開できます。1/(1+r)の形の場合は公比が-rになります。ここでは展開後の結果にz2を乗じていますが、初項がz2であるとしてz2/(1+z2)に対して幾何級数展開を適用しても最終的な計算結果は同じになります。
⑤定積分の計算と極限の考察
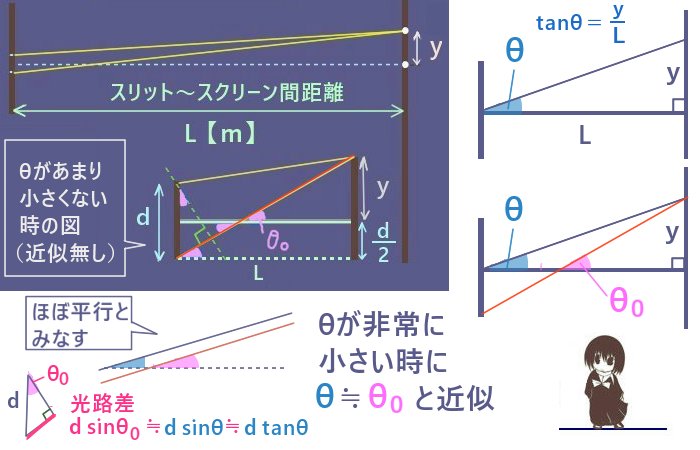
ライプニッツ級数は「四分円の面積π/4が無限級数1ー1/3+1/5-・・・に等しい」という式であり、四分円の面積は円の上半分の式\(y=\sqrt{2x-x^2}\)をx=0からx=1まで定積分すれば得られます。そのため本来は、上記で得られた積分の変形式でも積分変数xに対して積分区間を [0,1] としたいところです。簡易的な方法としてはそれでライプニッツ級数を導出可能です。
すなわち、x=0の時にy=z=0,x=1の時にy=z=1の関係から、得られている不定積分を定積分に変える事でライプニッツ級数を得ます。(積分中のxy,zxは共に積分変数をxとしている原始関数であり、例えばx=1を代入してyについてもその時にy=1なのでxy=1という計算。)
$$\frac{1}{2}\left([xy]_0^1+[zx]_0^1\right)-\left[\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right]_0^1=\frac{1}{2}\left(1+1\right)-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$
$$=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$
$$これが\int_0^1 y dx=\frac{\pi}{4}に等しいとすると\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$
しかしここでは一応、積分区間にx=0とx=1を含める事はできないとした場合の計算も記します。
- x=0を含めないのは、式変形で使用したdy/dxがx=0で無限大となるため
- x=1を含めないのは、幾何級数展開時に|z|<1の条件が必要なため
0<ε<δ<1であるεとδを考え、積分区間を[ε,δ]と置きます。そして計算結果においてε→0,δ→1の極限を考えます。ε→0の時y→0およびz→0であり、δ→1の時y→1およびz→1です。
ライプニッツ級数自体がπ/4に収束する「無限級数」なので、積分区間の極限を考えた時にも等式は問題なく成立します。四分円を普通に定積分した時に積分区間[ε,δ]に対してε→0,δ→1とすればπ/4に収束するので、「2つの式の極限値が同じ値に収束する」という事でライプニッツ級数の等式が成立します。
$$\int_\epsilon^\delta y dx=\frac{1}{2}\left([xy]_\epsilon^\delta+[zx]_\epsilon^\delta\right)-\left[\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right]_\epsilon^\delta$$
$$\lim_{\epsilon \to 0, \delta \to 1}[xy]_\epsilon^\delta=1\cdot1-0\cdot0=1,\hspace{7pt}\lim_{\epsilon \to 0, \delta \to 1}[xy]_\epsilon^\delta=1\cdot1-0\cdot0=1$$
幾何級数展開した部分についての極限については、何が問題なのかを整理しておきます。
- 幾何級数が収束する事が保証されるのは|z|<1の範囲(0<x<1)であり、級数が収束しないなら項別積分もできない。
- z=0(x=0)の時には幾何級数展開自体は可能で、1/(1+z2)に対して初項1だけが残り、z2=0を乗じて全体が0になる。従って、ε→0の時の全体の極限値も0。
つまり、考察が複雑になるのは積分区間の端点を1に近付けて行く場合です。より具体的には
z3/3ーz5/5+z7/7+・・・に「z=1を代入してみた場合の式」が収束するかどうかの判定が曖昧になっています。
この時にz3/3ーz5/5+z7/7ー・・・の形の無限級数が収束するかどうかは、実は独立に確かめる方法があります。z=1を代入してみた時の形1/3ー1/5+1/7ー・・・は収束する事を確認できます。(但し、その方法では1ー1/3+1/5ー・・・がπ/4に収束するかどうかは判定できません。)
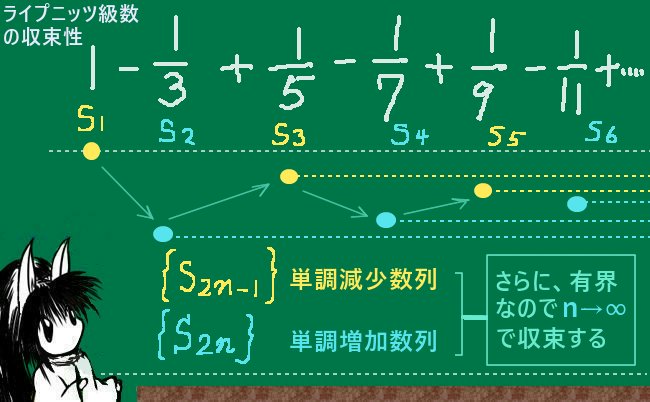
数列{an}について
・数列{|an|}が単調減少 かつ
・n→∞でan→0ならば
交代級数a1ーa2+a3ーa4+・・・は収束する。
(但しこの逆は真ではなく、交代級数が収束しても上記2条件が満たされるとは限らない。)
※微分に関する同名の「ライプニッツの定理」も存在し、状況によっては使用を避けたほうが良い名称です。
この判定方法によれば、1/3ー1/5+1/7ー・・・は「収束する」事が分かります。
■参考:交代級数の収束性の検証(1/3ー1/5+1/7ー・・・の場合。逆三角関数によるライプニッツ級数の導出過程にて。)
このような時にz3/3ーz5/5+z7/ー・・・はz→1の時に収束し、
その極限値は1/3ー1/5+1/7ー・・・の極限値に等しくなる事を保証する定理(連続性定理)がまた別に存在します。そのため、幾何級数展開した部分の極限は次のようになります。
$$\lim_{\epsilon \to 0, \delta \to 1}\left[\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right]_\epsilon^\delta=\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\cdots\right)-0$$
$$=\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\cdots$$
$$よって、\lim_{\epsilon \to 0, \delta \to 1}\int_\epsilon^\delta y dx=\frac{1}{2}\left([xy]_\epsilon^\delta+[zx]_\epsilon^\delta\right)-\left[\frac{z^3}{3}-\frac{z^5}{5}+\frac{z^7}{7}-\frac{z^9}{9}+\cdots\right]_\epsilon^\delta$$
$$=\frac{1}{2}(1+1)-\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\cdots\right)=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$
$$同時に、\lim_{\epsilon \to 0, \delta \to 1}\int_\epsilon^\delta y dx=\int_0^1 y dx=\frac{\pi}{4}であるから$$
$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$

■参考:(アーベルの)連続性定理
積分区間の端点の極限の考察で使用した連続性定理は次のようなものです。
x=0を中心とする整級数において収束半径がρ(>0)の時、
$$x=\rhoにおいて\sum_{n=0}^\infty a_nx^nが収束する\Rightarrow \lim_{x\to\rho -0}\sum_{n=0}^\infty a_nx^n=a_n\rho^n$$
$$\left(x=\rhoにおいて\sum_{n=0}^\infty a_nx^nが収束する\Rightarrow f(x)はx=\rho において左側連続\right)$$
xはρよりも小さい側からの極限を考えるものとしています。(「x→ρー0」の意味)
x=0を中心とする整級数(以下、単に「整級数」と呼びます)において収束円が(-ρ, ρ)であるという事は、|x|>|ρ|で収束しない事を意味します。
この時にもしx=ρにおいては整級数が収束する時に、その条件下で整級数が収束する範囲内でxを動かしてx→ρの極限を考えるとx=ρでの整級数(のnに関するxの極限関数)の連続性が保証されるというのが連続性定理の内容です。
この定理の表現方法はいくつか存在します。
例えば$$\sum_{n=0}^\infty a_nx^nが収束円の1つの端で収束する\Rightarrow\sum_{n=0}^\infty a_nx^nはその端において連続である$$と言っても同じ事です。
また、連続である事を表す極限については、例えば0以上1未満のtを使って\(\sum_{n=0}^\infty a_n(\rho t)^n\)に対してt→1の極限を考えても同じ事になります。
整級数の中には収束円の端点の片側だけで収束して、もう片方の端点では発散するというものが存在します。連続性定理もx=ρで整級数が収束する時にx=ρ側だけで連続性を保証し、
x=ーρの連続性は分からないものになります。
■連続性定理の証明
まず、各xでの整級数の極限関数がL(x)であるとします。
x=ρで収束するので
$$\sum_{k=0}^{\infty}a_k\rho^k =L(\rho)として、$$
$$任意の\epsilon>0に対して、n>Nであれば\left|\sum_{k=0}^na_k\rho^k -L(\rho)\right|<\epsilonとなる自然数Nが存在$$
$$b_0=a_0-L(\rho),\hspace{5pt}n\neq0の時はb_n=a_nとするとn>Nであれば\left|\sum_{k=0}^nb_k\rho^k\right|<\epsilon$$
次に|x|<|ρ|の任意のxに対しても、n>Nであれば一律に任意の同一のプラスの実数値以下(あるいは未満)にできるかを調べます。【εごとにxに依存しないで1つの値Nを決定できるかどうかを調べたい。】
$$n>M>Nに対して|S_n|=\left|\sum_{k=M+1}^nb_k\rho^k\right|=\left|\sum_{k=0}^nb_k\rho^k-\sum_{k=0}^Mb_k\rho^k\right|<2\epsilon\hspace{5pt}\cdots(*)$$
$$n> M+1の時S_n-S_{n-1}=b_n\rho^n\hspace{10pt}n=M+1の時、S_{M+1}=b_{M+1}\rho^{M+1}$$
$$x=\rho tとすると、\sum_{k=M+1}^nb_kx^k=\sum_{k=M+1}^nb_k\rho^kt^k=S_{M+1}t^{M+1}+\sum_{k=M+2}^n(S_k-S_{k-1})t^k$$
$$=S_{M+1}t^{M+1}+(S_{M+2}-S_{M+1})t^{M+2}+\cdots+(S_{n-1}-S_{n-2})t^{n-1}+(S_{n}-S_{n-1})t^n$$
$$=S_{M+1}(t^{M+1}-t^{M+2})+S_{M+2}(t^{M+2}-t^{M+3})+\cdots+S_{n-1}(t^{n-1}-t^n)+S_nt^n$$
|t|<1(すなわち|x|<|ρ|)の時はtk+1-tk>0であり、
削除: かつn>M>NであればSnに関して上記(*)式が成立するので次の不等式が成立します。
$$\small{\left|\sum_{k=M+1}^nb_kx^k\right|≦|S_{M+1}|(t^{M+1}-t^{M+2})+|S_{M+2}|(t^{M+2}-t^{M+3})+\cdots+|S_{n-1}|(t^{n-1}-t^n)+|S_n|t^n}$$
$$<2\epsilon(t^{M+1}-t^{M+2})+2\epsilon(t^{M+2}-t^{M+3})+2\epsilon(t^{M+3}-t^{M+4})+\cdots$$
$$+2\epsilon(t^{n-2}-t^{n-1})+2\epsilon(t^{n-1}-t^n)+2\epsilon t^n$$
$$=2\epsilon t^{M+1}<2\epsilon$$
【以上の不等式の組み立て方は級数変化法と呼ばれ、より一般的な形の命題が存在します。】
$$|x|<|\rho|である任意のxに対して、任意の2\epsilon>0を考えた時に$$
$$n>M(>N)であれば\left|\sum_{k=M+1}^nb_kx^k\right|=\left|\sum_{k=0}^nb_kx^k-\sum_{k=0}^Mb_kx^k\right|<2\epsilon$$
$$\left|\sum_{k=M+1}^nb_kx^k\right|=\left|\sum_{k=M+1}^na_kx^k\right|であるから【初項a_0,b_0がないので】、$$
$$n>M>Nであれば\left|\sum_{k=M+1}^na_kx^k\right|=\left|\sum_{k=0}^na_kx^k-\sum_{k=0}^Ma_kx^k\right|<2\epsilonでもある。\cdots(**)$$
今、整級数を関数列{fn}として見た時に、集合Fを{fn, fn+1, fn+2, ・・・}として考えて、
Fに対する上限と下限Bn=supFおよびAn=infFを考えます。
各xに対してn>Nの時、
任意のδ>0に対してBn-δ<fpとなる自然数p>Nがあり【上限の定義から】、
2ε=ε1>0に対して別の自然数q>Nを考えて上記(**)式でn=p,M=qとすると
|fp-fq|<ε1であり、-ε1<fp-fq<ε1
もしp<qならn=q,M=pとして考えて、成立する不等式は結果的に同じになります。
すると、Bn-δ<fp<ε1+fqとなり、Bn-fq<ε1+δ
1つのqとε1に対してδは0より大きい範囲で任意であるので、
Bn-fq<ε1は成立し、Bn-fq=ε1もあり得るけれども
Bn-fq>ε1は成立しないので
Bn-fq≦ε1・・・(***)
下限については任意のδA>0に対してAn+δA>fjとなる自然数j>Nがあり【定義から】、
先ほどの(***)式はq=jの時でも成立し、Bn-fj≦ε1⇔fj≧Bn-ε1となるので
An+δA>fj≧Bn-ε1であり、
An+δA>Bn-ε1⇔Bn-An<δA+ε1
δAは0より大きい範囲で任意なのでBn-An≦ε1
これはn→∞とした時にBn→Anを意味して、閉区間 [Bn,An] は1つの点{c}に収束します。
さらに、n>Nの範囲でBn≧c≧Anであるから、この時に任意のn>Nに対して|fn-c|≦ε1
(この範囲内でBn=Anでなければ|fn-c|<ε1)
よってcは整級数fnの極限値でもあり、各xに対してc=L(x)であり、
n>Nであれば|x|<|ρ|の範囲内の任意のxについて一律に|fn-L(x)|≦ε1=2εとなります。
またx=ρの時はn>Nでε未満になるので、2ε以下という不等式も満たします。
【この事は整級数が|x|<|ρ|およびx=ρにおいて一様収束する事を表しています。
また、(**)式を示した後の証明はコーシー列に関する考察の一部です。整級数に限らず一般の数列に対して成立する事も含んでいます。】
次にx=ρでの連続性を見るためにx→ρの極限を連続性の定義の式から考えると、
三角不等式の考え方を利用して
$$\small{\left|\sum_{k=0}^\infty a_kx^k-\sum_{k=0}^\infty a_k\rho^k \right|≦\left|\sum_{k=0}^\infty a_kx^k-\sum_{k=0}^na_kx^k \right|+\left|\sum_{k=0}^n a_kx^k-\sum_{k=0}^na_k\rho^k \right|+\left|\sum_{k=0}^n a_k\rho^k-\sum_{k=0}^\infty a_k\rho^k \right|}$$
右辺の絶対値記号内の3項はnの値やxの範囲により、それぞれがε未満か2ε以下になります。
【特にnについて考える時に、上記で示したようにxの値に関わらずn>Nであれば一律に不等式が成立する事が重要です。】
①右辺第1項について、整級数の一様収束性よりn>Nの時。(Nの値はxに依存しない。)
②右辺第2項について、有限の次数の多項式はx=ρで連続なので、x=ρを含む十分小さな開区間U内の任意のxに対して。【この項はx→ρの極限で、nの値は任意で成立。】
③右辺第3項について、x=ρにおいても整級数は収束するのでn>Nの時。
そこで、nが①と③を満たすように十分大きく、
xが②を満たす開区間U内の範囲にあり、かつ|x|<|ρ|であれば
$$\left|\sum_{k=0}^\infty a_kx^k-\sum_{k=0}^\infty a_k\rho^k \right|<2\epsilon+\epsilon+\epsilon=4\epsilon$$
$$\epsilonおよび4\epsilonは任意の小さな実数であるので、xの関数\sum_{k=0}^\infty a_kx^kはx=\rhoで左側連続。$$
ここでは(-ρ,ρ)の区間内でx=ρにおいて左側連続である事が示されています。もしマイナス側のx=-ρでも整級数が収束するなら、同様にx=-ρで右側連続である事を示せます。
【以上の証明は、いくつかの命題や補題に分けて説明される事もあります。】