電流は向きを持っていますが、電磁気学において3次元の空間の中での向きを持つベクトルとして扱う時にはむしろ電流密度ベクトルが扱われる場合が多いと言えます。「電流密度ベクトル」あるいは単に「電流密度」とも言われますが、いずれにしてもベクトルで表される量です。
電流は \(I\) の記号で書く事が多いですが、電流密度ベクトルは一般的に\(\overrightarrow{j}\) で表され、空間内の位置ごとに各成分がx,y,zの関数で表されるベクトル場です。(従って電流密度ベクトルに対する発散や回転も考える事ができ、成立する諸式が存在します。)
※電流の記号との紛らわしさを避ける目的で複素数の虚数単位 i をjで書く場合もありますが、ここで扱う\(\overrightarrow{j}\)は電流密度を表すので別物です。電流密度ベクトルの「大きさ」を表す時にはこのサイトでは\(|\overrightarrow{j}|\)として表記するか、もしくは\(J\)の文字を使う事にします。
電磁気学の中での位置付け
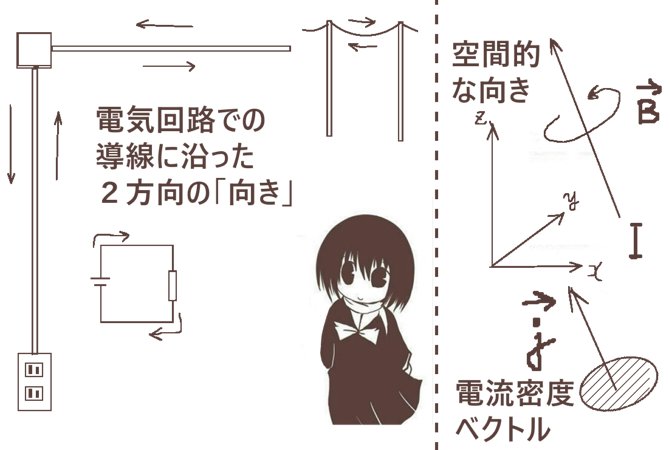
普通、電気回路における電流の向きは導線に沿って「片方向とその逆」だけを考えてプラスとマイナスで表します。これは、電圧との関係や電気エネルギーの消費に関して「導線の空間的な向き」というものが一般的にはほとんど影響しないためです。そのため、電気回路を考えるうえでは普通は電流を空間的な意味でのベクトルとしては扱わず、スカラー量として扱うのが基本です。
例外はあります。例えばコイルのように非常に狭い範囲でぐるぐる巻きになった形状の導線は交流の電気回路においてインダクタンスを持ち逆起電力を発生させる「素子」として扱われます。
しかし通常の導線部分に関しては、電線を地面に対して水平に設置しても垂直に設置しても斜めにしても、電流や電圧の量に基本的に影響しないのです。(これが水などが流れる流体回路であれば重力の影響がありますから話が変わってきます。)
また、あくまで数式的な問題ですが電気回路においても交流電流で位相(正弦関数の角度)と実効値の関係を模式的に表す方法として「ベクトル」を使用する事はあります。しかしそれは空間的な方向を表すベクトルではないのです。
他方で、より電磁気学的に見た時には電流も「空間的な意味での向き」を持つものとして扱う事は可能であるし、理論的な整合性のために必要な事でもあります。電場や磁場などと同じく、電流もベクトル場として扱う事は可能という事です。
ただし電磁気学では普通は「電流のベクトル」は敢えて考えずに、
代わりに「大きさが単位面積当たりの電流」であり、
向きは空間的な意味での電流の向きに等しい「電流密度ベクトル」を考えます。
(電流「密度」と言いますが大きさは「単位面積あたり」で考えます。)
この「電流密度ベクトル」は、電磁気学においては特に電荷保存則の式とアンペールの法則の微分形において重要です。それら2つについてはこの記事内でも解説をします。
電流密度ベクトルは、どちらかというと電気だけの考察ではなく、磁気のほうも合わせて考える事項に対して使われる事が比較的多いと言ってもよいかもしれません。
「電流をベクトルとして扱う方法」としては電流密度ベクトルを使う以外に、空間内の導線の接線ベクトルと電流の大きさを合わせた「電流要素」または「電流素片」をベクトルとして扱う事もあります。電流が作る磁場をベクトルとして直接表すビオ・サバールの法則では電流素片と電流密度ベクトルの両方での形が存在します。
電流密度ベクトルの定義と意味
電流密度ベクトルには一見すると2つの捉え方がありますが、それらは互いに無関係では無く、電磁気学では両方の考え方を組み合わせて考察がされます。
「単位面積あたりの電流」としての電流密度ベクトル
まず向きが空間的な意味で電流と同じで、
大きさが単位面積あたりの電流になるものを「電流密度ベクトル」と呼ぶ考え方から見てみます。
ある位置における電流密度ベクトル(あるいは単に「電流密度」)\(\overrightarrow{j}\)は
次のようなベクトル場です。
- 向き :電流の空間的な向き
- 大きさ:電流の空間的な向きに対して垂直な平面 での単位面積あたりの電流の大きさ
ただし、その面積を考える平面についてなのですが
電流の空間的な向きに対して「垂直な平面」で考えるというのは、要するに電流の向きに対して断面積を考えるという事です。電気回路での考察でもそうですが普通は導線の「断面積」と言ったら導線の向きに対して真っすぐ切れ目を入れて面積を考えるわけで、斜めに切って考えてはいけないわけです。ですからここでは、電流の向き空間的に対して斜めの平面ではなく「垂直な平面」である事を強調しています。この事は、のちの考察でも重要となります。
(※考えている面が電流密度ベクトルの向きに対して「斜め」になっている場合の考察も重要で、計算の考え方は後述します。)
後述しますように、電流密度ベクトルは「法線面積分」を考えたいので使っているというところもあり、さらにそれによって「電流」に対して電流密度ベクトルの形で発散や回転を考えていく事も可能になるという計算上の利点が生じます。

電流を電荷の流れとして考えた時の電流密度ベクトル
電流密度ベクトルには上記の意味はあるのですが
他方で電流が「電荷の流れ」であると考えると、
電流密度ベクトルは次のように表す事もできます。
電荷密度がρ[C/m3]で、分布する電荷全体の速度ベクトル\(\overrightarrow{v}\)がである場合には
電流密度ベクトルは次のようにも表せます。
$$\overrightarrow{j}=\rho\overrightarrow{v}$$
この捉え方での電流密度ベクトルは、実は次のようなベクトルです。
- 大きさ: ある面を単位面積あたり、単位時間あたりに通過する電荷の電気量
- 向き :空間的な意味での電流の向き(前述の定義と同じ)
電流の大きさとは「ある面を単位時間に通過する電荷の電気量」であるという考え方がもとになっています。
その観点から考察すると、実は上記の式で表した電流密度ベクトルの大きさに「ベクトルに垂直な面の面積」を乗じると「電流」になるという関係が成立します。これは、最初に考えた「単位面積あたりの電流」として電流密度ベクトルの大きさを考えた事と同じになっています。
このように電荷密度と速度で考えた場合には電流密度の単位に時間(秒[s])が含まれるはずですが、単位の決め方としてはむしろ電流のほうにそれが含まれると考えます。
すなわち、電流の単位について [A]=[C/s]と考えて、
電流密度の大きさの単位は [A/m2]で表します。[A/m2]=[C/(m2・s)]と変換はできます。
ところで、そもそも「電流」と呼んでいる量が何かの「流れ」である根拠は何か?という事については、後述にて簡単に触れます。
この考え方はある電荷密度の分布に存在する電荷の塊が動くという感じなのですが、一定の質量や体積を持った物体の運動と違って少しイメージが沸きにくいかもしれません。
そこで、次に見るように1つの位置の面(電流密度ベクトルに垂直とします)を基準にして
「1秒間で電荷の塊が、電気量の合計に換算してどれほどがそこを通過したか」という捉え方をすると少しは分かりやすくなります。
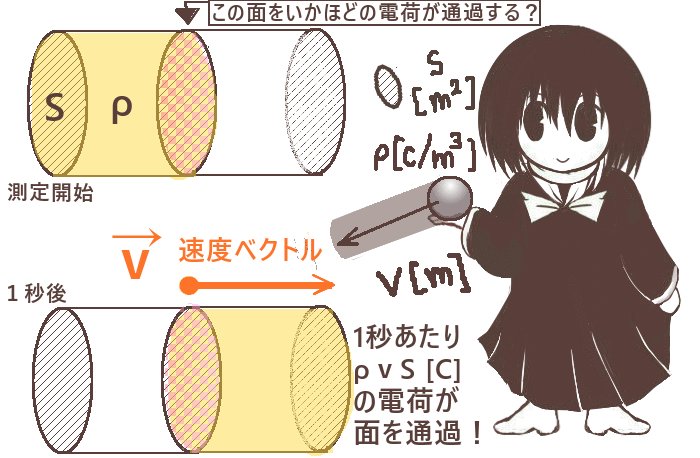
今、速度ベクトルの大きさ(=速さ)をvとします。
考えたい「面」はこの速度ベクトルに対しても垂直なものとしています。
そして面積Sの面のすぐ後ろに接した形で控えている電荷の分布が、
塊として面に対し垂直に「面を貫通する方向」に動くとします。
すると、1秒当たりに面を境に反対側に移動する電荷の電気量(これがすなわち電流です)は
「電荷密度ρ × 体積(vS)」としてρvSとなるわけです。
(単位は「1秒当たり」まで単位に含めれば [C/s]です。)
1秒間だけ電荷の塊を動かして、
止めた後に塊の先端がどこまで移動したかを計る事で「電荷密度×体積」の計算によって
「面を通過した電気量の合計」を電流は表していると捉える事ができます。
話を整理しますと、まず電流密度ベクトルを改めて次のように考えたわけです。
$$\overrightarrow{j}=\rho\overrightarrow{v}$$
この式のもとで、電流密度ベクトルの大きさは次のようになります。
$$\left|\overrightarrow{j}\right|=\rho v$$
そしてこの式の右辺ρvは先ほどの考察により、速度ベクトル面積を乗じる事により「電流」を表すと考える事ができるのでした。そこで上式の両辺に面積Sを乗じると次のようになります。
$$\left|\overrightarrow{j}\right|S=\rho vS$$
つまり「電流密度ベクトルの大きさ」×「ベクトルに垂直な平面における面積」=「電流」
の関係であり、最初に考えた電流密度ベクトルの定義の場合と同じ関係式が成立しているわけです。
面が速度ベクトルに対して斜めの時
ところで、そのように考えた時には
実は面に対して斜め方向に速度ベクトルが向いている時も同様に考える事ができます。
ややこしいようですが、
「電流密度ベクトルの大きさ」×「面積」=「電流」と考える時の面積は
電流密度ベクトルに対して垂直な面のものを考えますが、
電流の定義として「面を通過する電気量」と言う時は必ずしも垂直でなくてもよいと考えます。
その場合には、面に分布している電荷が一斉に次々にそこから斜め方向に移動していくと考えます。
すると、その場合は移動した電荷の電気量は「電荷密度×面積S×斜めの立体の高さ」です。
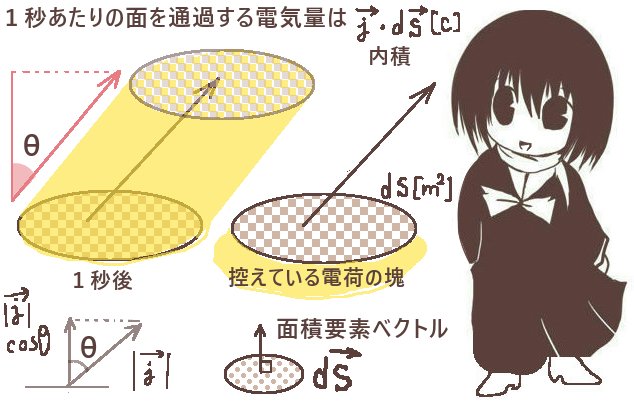
電荷密度ρと速度ベクトルの大きさ(=速さ)vの情報は電流密度ベクトルに含まれている事に注意すると、1秒間に面を通過した電荷の電気量は実は面積要素ベクトルと電流密度ベクトルとの内積で表す事ができます。「面積要素ベクトル」とは「微小領域の面に垂直で、大きさは微小面積dSである」というベクトルです。
これは、内積で使う余弦 cosθを速さvに乗じる事により1秒後に電荷の塊が通過してできる体積の「高さ」が計算できて、さらに底面積のdSに乗じれば体積が計算されるためです。
そして、体積が分かれば電荷密度ρを乗じて「1秒当たりに面を通過した電気量」すなわち電流が分かる事になります。
電荷密度ρで分布する電荷が一斉に速度\(\overrightarrow{v}\)で運動しているとします。
この時に面積がdSの微小面を1秒あたりに通過する電荷の電気量(つまり電流)は、
面の向きに関わらず電流密度ベクトルと面積要素ベクトルの内積を使って次式で表せます。
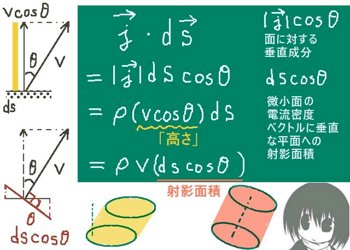
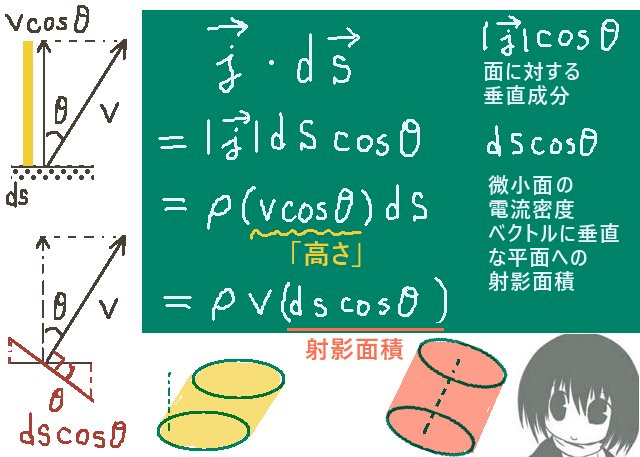
$$Q=\overrightarrow{j}\cdot d\overrightarrow{S}=\left|\overrightarrow{j}\right|\hspace{2pt}\left|d\overrightarrow{S}\right|\cos\theta$$
$$=\rho (v\cos\theta)dS$$
面積要素ベクトルは微小面に対して「垂直」なベクトルなので、角度θの位置関係には注意。
この式は電流密度ベクトル(および速度ベクトル)が面に垂直な場合も含めて使えるので、
一般に微小面を単位時間当たりに通過する電荷の電気量(=電流)を表す式になります。
ここで、内積計算では余弦を電流密度の大きさと面積要素のどちらに乗じても結果は同じです。
すると上式は数式上、
「電流密度ベクトルの、面に対する垂直成分とdSの積をとる(面に垂直な体積として計算)」
「面を電流密度ベクトルに対して垂直な平面に射影して、その射影面積とvρの積をとる」
といった解釈をしてもよい事になります。
$$Q=\left|\overrightarrow{j}\right|\hspace{2pt}\left|d\overrightarrow{S}\right|\cos\theta=
\left(\left|\overrightarrow{j}\right|\cos\theta\right)
\left|d\overrightarrow{S}\right|
$$
$$=\left|\overrightarrow{j}\right|
\left(\left|d\overrightarrow{S}\right|\cos\theta\right)
$$
電流とはそもそも何なのか?「電荷の流れ」とみなせる根拠は
ここで、そもそも電流とは「電荷の流れ」なのか?という疑問も生じるかもしれません。その話はまた長くなりますが興味深い議論でもあります。ここではそのように見なせる事を支持する実験事実や理論的根拠をいくつか列挙しておくに留めます。
- 陰極線の実験:真空中でつながっていない電極間に高電圧をかけると、光の筋が見える。この光の筋は電場をかけると曲がり、磁場によっても曲がる(ローレンツの力を受ける)ので「電荷を持った運動する」であると解釈できる。正確にはこれは電極から飛び出した電子線の流れだが「電荷を持つ粒子の流れ」の実例となっている。
- コンデンサーの放電電流:静電気を帯びた物体は、短い時間だけだが電流が生じさせる事ができ、電流発生後では物体が帯びていたはずの静電気が無くなっている。
これは蓄えられていた電荷が「流れ出た」のではないかと見れる。コンデンサーとは2枚の電極で薄い絶縁物を挟んだ電気回路の素子で、電荷を蓄えたり放出したりする。 - 導線中の電流は導線の空間的向き以外の「導線に沿った一方向とその逆向き」の2方向の「向き」を持つ。電流の向きが異なれば発生する磁場の向きも逆転する、また、電流を発生させる電源につなぐ2つの端子を入れ換える事で、電流の向きが逆になる事が確認できる。
水などの流体も管の中での流れは一方向とその逆向きの2方向ある。 - 電気回路においてはキルヒホッフの法則として、導線の分岐があった場合には電流も「分岐前の電流=分岐後の電流の総和」となる事が確認できる。これは水などの「流体の流れ」で見られる性質。(電流の量は発生する磁場の大きさから確認可能。一般的な電流計もそのようにして電流を測定しています。)
- 化学電池では化学反応が必ず起きていて、電荷の流れが「電子の流れ」に由来するものであると捉えると、化学反応における理論との整合性もとれる。
電流密度の法線面積分と、電流の総和との関係の式
特定の曲面を通過する電流の総和を考える時、
電流密度ベクトルによる法線面積分を使う方法があります。
これは、曲面上のある微小領域を通過する電流は、電流密度ベクトルと面積要素ベクトル(微小領域に垂直な向き)との内積で表せるという事を根拠にしています。ここでの微小領域は電流密度ベクトルに対して一般的には垂直ではなく「斜め」になっている事に注意が必要となります。
電流及び電流密度ベクトルが曲面上で連続的に分布しているとして、曲面全体で法線面積分を考える事によって曲面を通過する電流の総和を表す事ができます。
ある曲面Sを「通過する」(=貫通する)電流が連続的に分布している時、
その電流の総和は電流密度ベクトルの法線面積分によって表す事ができます。
$$I_S=\int_S\overrightarrow{j}\cdot d\overrightarrow{s}$$
この式を考える曲面は開曲面でも閉曲面でも可です。
「電流が連続的に分布している」と書きましたが、
「電荷の流れが生じている」と考えても同じです。
(ここでは渦電流のように表面上をまわるような電流ではなく、「面を貫通する向き」の電流の分布を想定しています。曲面に接する向きの電流も考える事はできますが、その分の量に関してはここでは内積計算により0として扱われます。)
法線面積分では、面積要素ベクトルは大きさは微小領域の面積であり、向きは微小領域に対して垂直な向きのベクトルとして考えます。
この式は、内積の見方によって2つの見方ができます。
すなわち余弦を微小面積に乗じて射影面積を考えていると見るか、電流密度ベクトルの大きさに乗じると見るかの違いですがどちらで考えても結果は同じというのが本質です。
どちらにしても、\(\overrightarrow{j}\cdot d\overrightarrow{s}\) という量は微小領域における電流を表します。
まず、積分を行う曲面を多数の微小平面に分割します。(例えば曲面上の3点を結ぶと確実に三角形状の微小な平面領域ができるので多数の点を考えて分割します。)
微小領域の射影を考える場合
微小領域において一般的には面が電流密度ベクトルに対して垂直ではないので、単純に微小面積を乗じても正しい電流の値が出ません。しかし、前述の考察で見たように内積を考える事で、
位置関係的に微小面積dscosθは電流密度ベクトルに垂直な平面への射影面積になります。
よって、\(\overrightarrow{j}\cdot d\overrightarrow{S}==\left|\overrightarrow{j}\right|
\left(\left|d\overrightarrow{S}\right|\cos\theta\right)\)は曲面上の微小領域あたりの電流を表します。
ただし、曲面の領域の分割を十分多くしないと微小領域を平面に近似する事はできませんから、極限をとって積分として考える必要があります。それによって曲面上に分布する(ベクトルの向きを考えれば「通過する」)電流の総和を得るわけです。
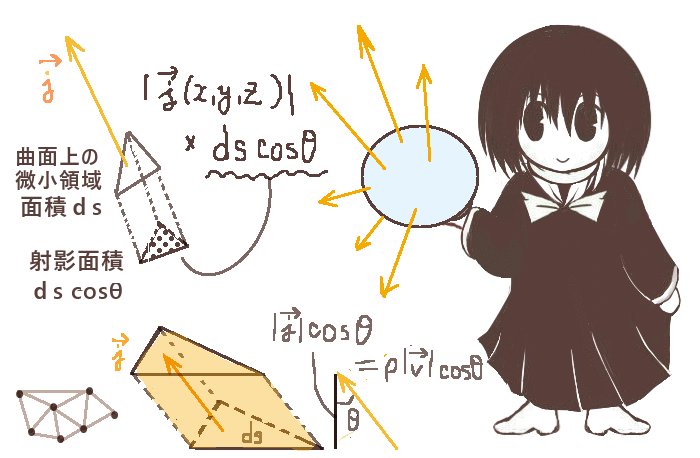
面を通過する電気量として考える場合
次に、電流密度ベクトルに対して垂直ではなく斜めになっている面に対して
「単位時間あたりに通過する電荷の電気量」を考えても同じ結果を得ます。
前述の「電流を電荷の流れと考える」時の考察により、
電流密度ベクトルと面積要素ベクトルの内積は「微小面(角度を問わず)を単位時間あたりに通過する電荷の電気量」です。すなわちそれはその微小領域における電流の大きさだと考えられるわけです。
$$\overrightarrow{j}\cdot d\overrightarrow{S}=\left|\overrightarrow{j}\right|\hspace{2pt}\left|d\overrightarrow{S}\right|\cos\theta$$
$$=
\left(\left|\overrightarrow{j}\right|\cos\theta\right)
\left|d\overrightarrow{S}\right|=\rho (v\cos\theta)dS$$
法線面積分の内積の部分については「余弦が電流密度ベクトルの大きさに乗じられている」と見ます。
さらに、余弦が速度ベクトルの大きさ(速さ)に乗じられていると見れば、\(v\cos\theta\) が1秒あたりの電荷が通過した体積の「高さ」になっています。さらに電荷密度と面積を乗じれば電流になるわけです。
曲面全体で微小領域における電流の合計を考えて、分割を十分多くとった極限として積分を考える必要があるのは先ほどと同じです。
このようにして、\(I_S=\large{\int_S}\overrightarrow{j}\cdot d\overrightarrow{s}\)が成立します。
電荷保存則の式
電流を電流密度ベクトルの法線面積分で表す方法において、閉曲面を考えます。
そこで、電流を電荷の流れの量として見る時には曲面の外に出ていく電気量もあるけれども内側に入って行く電気量もあり得るわけです。
いずれにしても、単位時間あたりに曲面の内側の領域全体の電荷の量には変化が生じます。
(その変化が「合計すると0」という事もあり得ますが、それも含めて「変化」としておきます。)
そこで、曲面の内側の全電荷を電荷密度で表します。
(これは電場に関するガウスの法則で行うやり方と同じです。)
$$閉曲面S内部の全領域Vの電荷の合計値は、Q_S=\int_V\rho dv$$
その量の単位時間当たりの変化量を微分によって考えます。
これは偏微分になりますが、積分変数(dv=dxdydz)とは異なる変数なので、「積分全体」を微分したものと「微分したものを積分」したものは同じ結果になります。(※積分領域に関数の不連続点が無ければ、これは数学的にやってよい計算です。領域の形や電荷密度の分布と関数形については不連続点が生じるような変なものを考えない必要はあります。)
$$\frac{\partial }{\partial t}Q_S=\frac{\partial }{\partial t}\int_V\rho dv=\int_V\frac{\partial \rho}{\partial t}dv$$
この式は「曲面の内部で電荷が増えたらプラス」としています。他方、電流密度の法線面積分で電流を表す方法では「曲面の外部で電荷が増えたらプラス」としています。
そのため、両者は「符合を入れ換えて」から等号で結ぶ事ができます。
$$\int_S\overrightarrow{j}\cdot d\overrightarrow{s}=-\int_V\frac{\partial \rho}{\partial t}dv$$
これは電荷の保存を表す式であり、「電荷保存則」のように呼ぶ事もあります。
要するに、内部で減ったものは外部では増えており、逆に内部で増えたものは外部では減っており、
「内部と外部の合計では一定値が保たれる」事を意味します。
もっとも、この「電荷の保存」自体(つまり2式を等号で結んだ事)に関しては何かから導出したというよりは、基本法則として考えて式で表したという性質のものと言えます。
次に、ガウスの発散定理を使って電荷保存則の式を書き替えます。(これは「ガウスの法則」ではなく、法線面積分と体積分の関係を表す「ガウスの発散定理」です。単に「ガウスの定理」「発散定理」とも言います。)ここでの曲面は「閉曲面」としているので定理が適用できる事に注意。
$$ガウスの発散定理により、\int_S\overrightarrow{j}\cdot d\overrightarrow{s}=\int_V \mathrm{div}\overrightarrow{j}dv$$
よって電荷保存則は次のようにも書けます。
$$\int_V \mathrm{div}\overrightarrow{j}dv=-\int_V\frac{\partial \rho}{\partial t}dv=\int_V\left(-\frac{\partial \rho}{\partial t}\right)dv$$
ここで、領域Vは条件を満たす範囲で(先ほどの連続に関する事など)任意の形状であり得るので、積分の中身も一致する事になります。よって、電荷保存則の微分形の形が得られます。
$$\mathrm{div}\overrightarrow{j}=-\frac{\partial \rho}{\partial t}$$
この形の式は流体力学でも使われ、一般的に「連続の方程式」とも言います。
閉曲面内部の電荷の時間変化が無い場合、すなわち∂ρ/∂t=0の時(外部への電流の出入りについても大きさに時間変化が無いので定常電流の時)には電流密度ベクトルの発散も0です。
つまり電流が定常電流である時には、電流密度ベクトルはベクトル場としては「湧き出しが無い」事が式で表現されます。
アンペールの法則で使う電流密度ベクトル
アンペールの法則は、マクスウェル方程式の中でも電流密度ベクトルとの関係が深い式です。それは元々、電流と磁場の関係を表す法則である事に由来するのですが、ベクトルとしては「電流」をそのまま扱うのではなく、「電流密度ベクトル」で考えたほうが都合が良い事が式を表しやすいのです。
アンペールの法則の微分形の導出の概要
アンペールの法則の周回積分の形を変形して、
法則の微分形を導出する過程で電流密度ベクトルを考える方法があります。まず、時間変化しない定常電流の範囲でアンペールの法則の周回積分側の式をストークスの定理で書き換えます。
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s}(=\mu_0 I)$$
Sは開曲面で、閉曲線Cを外縁に持つ条件のもと「任意の開曲面」になります。このような形になるので、法則の微分形を得るために電流を「何かの法線面積分で書けないか」と考えるわけですが、ここで電流を電流密度ベクトルの法線面積分で表す式が使えます。
$$I=\int_S\overrightarrow{j}\cdot d\overrightarrow{s}であるので、$$
$$\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s}=\mu_0 I=\int_S\left(\mu_0\overrightarrow{j}\right)\cdot d\overrightarrow{s}$$
$$Sは任意の開曲面なので\mathrm{rot}\overrightarrow{B}=\mu_0\overrightarrow{j}$$
このように、静磁場の回転が電流密度ベクトル定数倍に等しいという結果が得られました。
これが「定常電流における」アンペールの法則の微分形です。
この場合に発生する静磁場は直線電流に垂直な平面にだけ成分を持ちますが、
実際に具体的な計算をすると\(\overrightarrow{B}\cdot \overrightarrow{j}=0\) となる事や、電流の向きをz軸にとった時には磁場の回転がz成分以外の成分が0になる事などが確かめられます。
電荷保存則にしてもアンペールの法則の微分形にしても、電流をベクトルとして直接的に扱うよりも「電流密度ベクトル」で考えたほうが計算がしやすいという事情が見えてくるのではないでしょうか。
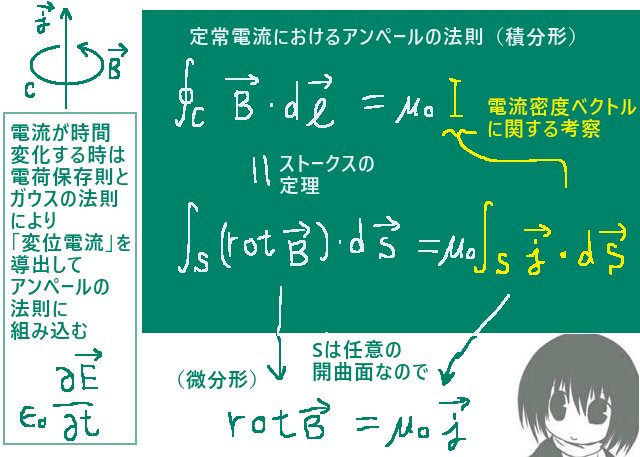
電流の時間変化がある時のアンペールの法則の概要
ところで電流の時間変化がある時のアンペールの法則はどうなるのかというと、電場の時間変化を含む項(変位電流)が加わります。アンペールの法則の「修正」ともよく言われます。
この変位電流とは電場の変化であって「電荷の流れ」ではないので普通の電流とは区別されるものではありますが、例えば電気回路でコンデンサーによって電流としては絶縁部分になっているところの電場の変化などを指します。
簡単にだけ述べると、まず先ほどの電荷保存則の微分形において、電荷密度の部分をガウスの法則の微分形によって電場に書き換えます。(これは「ガウスの発散定理」ではなく「ガウスの法則」です。)
$$\mathrm{div}\overrightarrow{j}=-\frac{\partial \rho}{\partial t}=–\frac{\partial}{\partial t}\left(\epsilon_0\mathrm{div}\overrightarrow{E}\right)$$
最右辺を左辺に移行して、発散を2つの項に作用させると考えると次式です。
$$\mathrm{div}\overrightarrow{j}+\frac{\partial}{\partial t}\left(\epsilon_0\mathrm{div}\overrightarrow{E}\right)=0\Leftrightarrow \mathrm{div}\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)=0$$
「磁場の回転」に対する発散は必ず0である事に注意して、定常電流におけるアンペールの法則の微分形にこの式を使い、さらに積分形のほうもこの式で書き直したものが電流の時間変化がある時のアンペールの法則の式です。
電流の時間変化がある時のアンペールの法則の微分形と積分形を書くと次のようになります。
$$\mathrm{rot}\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)$$
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\mu_0\int_S\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\cdot d\overrightarrow{s}$$
積分形のほうに関しては、電流密度ベクトルの部分を積分すると電流の大きさになるのでその項が定常電流の場合のアンペールの法則の電流の部分になります。
補足事項
説明した式の一部のナブラ表記
以上で説明した電流密度ベクトルを含む式で、
div, rot の記号の代わりにナブラ記号で書いたものを補足としてまとめておきます。
電荷保存則の微分形
$$\nabla\cdot\overrightarrow{j}=-\frac{\partial \rho}{\partial t}$$
特に、領域内の電荷の変化が無い場合(電荷の流れ=電流は一定値)には
電流密度ベクトルは発散が0で、湧き出しがありません。
$$\nabla\cdot\overrightarrow{j}=0$$
定常電流の場合において\(\nabla\cdot\overrightarrow{j}=0\)である事は、アンペールの法則からも導出可能です。
電流の時間変化が無い時 $$\nabla\times\overrightarrow{B}=\mu_0\overrightarrow{j}$$ 電流の時間変化がある時 $$\nabla\times\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)$$
マクスウェル方程式から電磁波の式を導出する過程などでは、電流密度ベクトルの回転を考える事もあります。それは回転を含む式であるアンペールの法則と電磁誘導の式に対して改めて回転を考える計算に由来します。
補足2:その他の電流密度ベクトルの使用例
この記事では扱っていませんが、
静磁場のベクトルポテンシャルは電流密度ベクトルを使って表されます。
また同じく、磁場に関する法則のビオ・サバールの法則は電流を使った形と
電流密度ベクトルを使った2つの形があります。
静磁場のベクトルポテンシャル(発散が0の条件のもとでの式)
$$\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j}}{R}dv$$
ビオ・サバールの法則の形の1つ
(積分の中の「×」記号は「回転」ではなく外積ベクトルを表す記号)
$$d\overrightarrow{B}=\frac{\mu_0}{4\pi}\frac{\overrightarrow{j}\times \overrightarrow{r}dv}{r^3}$$
これら2つの関係式・法則はいずれもアンペールの法則との関わりがあります。