ナブラ記号の使い方

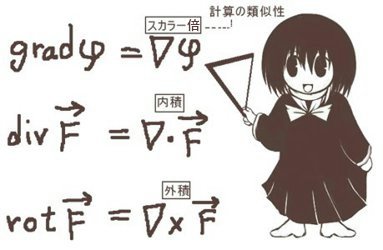
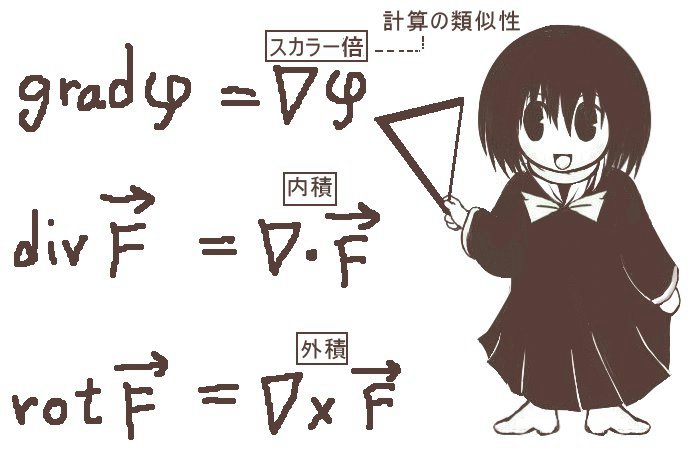
ベクトル解析などで使う grad, div, rot (または curl) の代わりに∇（「ナブラ」nabla, del）という記号を演算子として使って表記する方法があります。

この記事ではそれらの書き換えの方法と、ナブラ記号を使って作られる別の２つの演算子について詳しく説明します。

■サイト内参考記事（主に応用・ナブラを使う例など）
物理学全般で使用され、例として電磁気学で使う事ができます。

• 電磁場の波動方程式と真空中の電磁波の式
• 電磁誘導の法則
• アンペールの法則
• 電流密度ベクトル（および電荷保存の式など）

ナブラを使う利点は何か？

grad, div, rot の代わりにナブラ記号を使う利点は、特に式が複雑になる時などです。記述する文字数が少なくなるので比較的見やすくるといった事などの利点があります。

また数式の記述に統一性が出るために意味で好んで使われる場合もあるのです。後述していくように、grad, div, rot などの計算はベクトルの演算に類似性が見られるのでそれをナブラ記号によって統一的に整理する事も可能になるからです。

ただし grad, div, rot の置き換えとしての使用ではあくまで記号の「書き換え」なので数学的な意味が変わってしまうという事ではありません。

ナブラ記号を使わない grad, div, rot の表記法ではイメージ的な意味がつかみやすいという利点があります。言い換えると、一度イメージがつかめたのであれば数式的な形の簡便さや統一性を重視してナブラ記号での表記を行うという考え方もあると言えるでしょう。

尚「ナブラ」という言葉自体は元々楽器の「竪琴」の意味らしく、逆三角形の記号の形∇として見立てたというのが通説のようです。

勾配(grad)の書き換え

まずスカラー場に対して「勾配」を表す grad の書き換えです。

スカラー関数ｆ（ｘ，ｙ，ｚ）に対して gradｆの代わりに∇ｆと書いても同じ意味を表す約束になっています。

ｇradｆ＝∇ｆはベクトルなので成分を持ちますが、個々の成分を表す時には下に添え字を付けて表記する時があります。すなわち、∇ｆのｘ成分は∇_ｘｆ，y成分は∇_ｙｆ，ｚ成分は∇_ｚｆのように書いたりします。

$$\large{\mathrm{grad}f(x,y,z) =\nabla f=(\nabla_x f,\nabla_y f,\nabla_z f)}$$

例としては、ベクトル場がポテンシャル（スカラーポテンシャル、位置エネルギー）の勾配で表される式を書く時には記号として grad の代わりに∇を使えるわけです。

$$\overrightarrow{F}=-\mathrm{grad}\phiの代わりに\overrightarrow{F}=-\nabla\phiとも書けます。$$

この意味で使うナブラ記号はハミルトン演算子と呼ばれる時もあり、
形式的には「ベクトルとスカラーの積」として捉えられます。
※これは量子力学におけるハミルトン演算子もしくはハミルトニアンとは別物です。

あくまで形としての話ですが∇を数式上ベクトルとみなし（ベクトルそのものではない）、スカラー場との「積」のように考えるわけです。この考え方は、次に見るように発散や回転の書き換え時には「内積」や「外積」との数式上な類似性に着目する事との統一性を持っています。

$$形式的に、\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)ともみなせます。$$

発散（div）の書き換え

次に、ハミルトン演算子としてのナブラ記号を使ってベクトル場の「発散」div を書き換える方法を見ます。（※極限における「無限大への発散」は別物です。）

この場合には、発散 div がハミルトン演算子とベクトル場との「内積」のような形をとる事に着目します。そこで形式上の「∇とベクトル場の内積」を考えてベクトル場の発散を表すものと約束します。

$$\mathrm{div}\overrightarrow{F}の代わりに\nabla\cdot\overrightarrow{F}とも書けます。$$

$$\mathrm{div}\overrightarrow{F}=\nabla\cdot\overrightarrow{F}=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}$$

形式上という事は強調されるべきですが
勾配 grad は「スカラー場からベクトル場を作る」操作であり、
発散は逆に「ベクトル場からスカラー量を作る」操作である事を考えると
「ベクトルとスカラーの積はベクトル」であり
「ベクトルとベクトルの内積はスカラー」という、ベクトルの基本演算との類似性や統一性を見れるわけです。

例としてはガウスの発散定理は次のように書いてもよいわけです。

$$\int_V\nabla\cdot\overrightarrow{F}dv=\int_S \overrightarrow{F}\cdot d\overrightarrow{s}$$

ここで、左辺の積分の中身は\(\mathrm{div}\overrightarrow{F}\)であり、それに対して右辺の内積記号は図形的にも内積を考えますので数式的な形は同じでも意味が異なるわけです。この事に対して意味的に紛らわしいと見るか、数式上の統一性があって好ましいと見るかは人それぞれの考え方によるでしょう。

規則性に類似点は見られるとはいえ勾配と発散は異なる数学的な操作を表しますから、単独のナブラ「∇」とドットがついた「∇・」はそれぞれ意味としては別々の操作を表す事になります。

また、後述しますが少し紛らわしい表記として「∇・」ではなくナブラ記号とベクトル場の「内積の順序を変えたもの」は別の意味を表す演算子とみなす場合があります。通常のベクトルの場合は内積は順序を変えても同じスカラーになりますが、ナブラ記号を演算子として考えた場合には「∇・」の順番で書いて「発散 div」の意味になります。

$$\nabla\cdot\overrightarrow{F}=\mathrm{div}\overrightarrow{F}ですが、\overrightarrow{F}\cdot\nablaは別の演算子です。$$

回転（rot, curl）の書き換え

ベクトル場の回転をハミルトン演算子としてのナブラ記号で書き換える場合には３次元ベクトルの外積（クロス積、ベクトル積）の記号を使います。
つまり\(\nabla\times\overrightarrow{F}\)のように書くわけです。

$$\mathrm{rot}\overrightarrow{F}=\nabla\times\overrightarrow{F}$$

３次元ベクトルの外積はまた１つの３次元ベクトルですが、ベクトル場の回転もまた別のベクトル場ですから記述上の統一性があります。

通常のベクトルの場合、外積あるいはクロス積の成分での計算は次のようになります。

$$\overrightarrow{E}\times\overrightarrow{F}=(E_2F_3-E_3F_2,\hspace{5pt}E_3F_2-E_2F_3,\hspace{5pt}E_1F_2-E_2F_1)$$

この外積における最初のベクトル\(\left(\overrightarrow{E}のほう\right)\)をハミルトン演算子としてのナブラ記号で置き換えると、数式の形としてはベクトル場の回転になるわけです。

$$\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)のもとで$$

$$\nabla\times\overrightarrow{F}=\left( \frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z} ,\hspace{5pt} \frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x} ,\hspace{5pt} \frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y} \right)$$

見た目としては、∇を先に書いて偏微分する変数が「下側」に書かれますので順番を間違えないように注意。「偏微分の演算子」をベクトル場の各成分に付けると考えたほうが順番的には通常のクロス積との見た目の整合性が取れます。

$$\frac{\partial }{\partial y}F_3=\frac{\partial F_3}{\partial y}に注意して$$

$$\nabla\times\overrightarrow{F}の第１成分は\frac{\partial }{\partial y}F_3-\frac{\partial }{\partial z}F_2と考えます。$$

使用例としてストークスの定理をナブラ記号で書くと次のようになります。

$$\oint_C\overrightarrow{F}\cdot d\overrightarrow{l}=\int_S\left(\nabla\times\overrightarrow{F}\right)\cdot d\overrightarrow{s}$$

この式の右辺のように、ベクトル場の回転に「内積」が続くような場合には括弧をつけて\(\left(\nabla\times\overrightarrow{F}\right)\) のように書く事が多いです。そのまとまりで１つのベクトルである事を強調するわけです。括弧を付けないで内積を書く事もありますが、意味としては「ベクトル場の回転」と別のベクトルとの内積です。式の形から紛らわしい場合には括弧を付けておいたほうが無難かとは思われます。

「外積」という用語やその計算規則についてはベクトル場の回転を含む事項（例えばストークスの定理）を純粋に数学の解析学的に取り扱う場合にも重要になってきます。

２階の偏微分を扱う「ラプラス演算子」

以上の３例の他に「３変数の各々により２階の偏微分を行い加え合わせる」という操作が行われる時があります。つまり、ベクトル場の発散を１階ではなく２階の偏微分で行うような場合です。これは、スカラー場に対して行う場合とベクトル場に対して行う２つの場合があるので区別して説明します。

いずれの場合もナブラ記号を使って書く方法があります。
∇^２あるいは∇・∇と書いて１つの演算子としてみなし、「ナブラ２乗」と読むかラプラス演算子と呼びます。∇^２φのようにスカラー場やベクトル場に作用させて使います。

スカラー場に対する場合の例は次のようなものです。

$$\nabla^2\phi=\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}のような量を考えます。$$

ラプラス演算子の表記上の注意点

ラプラス演算子について∇^２という記号の代わりに、単独の三角形の記号「△」を使う事もあるので注意する必要があります。つまり、ナブラ記号を使わず、grad, div のような名称を元にした記号とも異なった、全く別の記号が改めて使われる事もあるという事です。

$$例：\nabla^2\phi=△\phi=\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}$$

さらにはラプラス演算子としての△記号は、書籍によっては微小量を表す「デルタ」Δ（これはギリシャ文字の１つ）との表記上の区別もつけられない場合もあります。そのため、書籍によっては記号の意味をきちんと押さえていないと数式の読み取りが非常に難しくなる場合があります。

デルタとラプラス演算子の記号が区別されない表記方法の場合、基本的にデルタはΔx（デルタエックス）などのように「変数」に付ける事が多く、ラプラス演算子は３変数の関数に付ける事からおおよその区別は可能です。つまり微小量の議論の文脈が無い箇所で唐突に３変数関数に対して△φなどと式に書かれたらそれは普通はラプラス演算子による計算を表します。

スカラー場に対するラプラス演算子

スカラー場の各成分に対して「２階の偏微分を行って加え合わせる」量は、スカラー場から始めて発散と勾配を組み合わせて作る事ができます。すなわち、あるスカラー場φに対してgradφを考え、その発散をとればよい事になります。

$$\mathrm{div}(\mathrm{grad}\phi)=\mathrm{div}\left(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z}\right)=\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}$$

この事自体をナブラ記号で書く事もできるのです。

$$\nabla\cdot(\nabla\phi)=\nabla\cdot\left(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z}\right)=\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}$$

そこで、ナブラ記号による演算の組み合わせである∇・∇を考えます。注意点として、これは∇・（∇φ）のナブラをくっつけてしまうというよりは、ハミルトン演算子同士の形式上の「内積」を考えて、それをスカラーのように考えてスカラー場φに乗じるという考え方に近いものです。（後述するスカラー演算子と同じ考え方です。）

また、そのように考えた∇・∇を∇^２と書く事もあります。いずれにしてもこれを１つの演算子とみなしてラプラス演算子と呼ぶわけです。

$$\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)同士の形式上の「内積」を考えます。$$

$$\nabla\cdot\nabla=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$$

$$あるいは\nabla\cdot\nablaを\nabla^2と表記して\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$$

∇・∇と∇^２を同じ意味で使う事に関しては、普通のベクトル同士の内積をとる時にはそれは「自乗」とはみなしませんので注意は必要です。（ベクトル同士の内積は「ベクトルの絶対値」の２乗にはなります。また、細かい点ではありますが曲線座標をもし考える場合には∇・∇と∇^２は同一視しません。）

このスカラー的な演算子（内積はスカラーである事にも注意）をスカラー場φに乗じるように作用させる事で∇・（∇φ）と同じ結果を得るというわけです。

$$\nabla^2\phi=\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)\phi=\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}$$

スカラー場に対してラプラス演算子を作用させる例としては微分方程式としての波動方程式があります。（解が周期関数のような「波動」になる。）また、演算子の部分だけをとって波動演算子と呼ぶ事もあり、そこにラプラス演算子が使われるというパターンもあります。

$$例：\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2} \right)\phi=-\frac{\rho}{\epsilon_0}$$

$$\left(\Leftrightarrow \nabla^2\phi-\frac{1}{c^2}\frac{\partial^2\phi}{\partial t^2} =-\frac{\rho}{\epsilon_0}\right)$$

この例は、電場に関するガウスの法則で電場の代わりにスカラーポテンシャル（これはスカラー場）を使って変形したものです。c は光の速さでｔは時間、右辺の記号は電荷密度と真空の誘電率。
ポテンシャルを使わず電場のままでも同様の式を導出できますが項などが増えて少しばかり複雑さが増します。同じ型の式を磁場についても導出できて、合わせて電磁波の式を導出できます。

ベクトル場に対するラプラス演算子

ラプラス演算子∇^２は、スカラー場だけでなくベクトル場にも作用させる事ができます。勾配はスカラー場に対して、発散と回転はベクトル場に対して必ず作用させるものである事と比較すると少し特殊であるとは言えます。しかし、通常の微分や偏微分の操作を演算子として考えると同じくスカラー場にもベクトル場にも作用させる事ができますからそれほど不思議な考え方ではないとも言えます。

そして、考え方自体はラプラス演算子をスカラー場に作用させる時と同じなのです。つまり、∇^２あるいは∇・∇はスカラー的な演算子と言えるからベクトル場にも作用できると考えるのです。そのため、ラプラス演算子をベクトル場に作用させたものもまたベクトル場になります。演算子がスカラー量の乗法のように「ベクトルの各成分に対して作用する」と考えるためです。

計算上は演算子の作用により一度３つのベクトルができて、合計して結果的に１つのベクトルになると考える事も可能です。いずれにしても最終的にはベクトル場の成分に対して作用する計算です。具体的には次のようになります。

$$\nabla^2\overrightarrow{F}=\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)\overrightarrow{F}=\frac{\partial^2}{\partial x^2}\overrightarrow{F}+\frac{\partial^2}{\partial y^2}\overrightarrow{F}+\frac{\partial^2}{\partial z^2}\overrightarrow{F}$$

$$=\small{\left( \frac{\partial^2F_1}{\partial x^2}+\frac{\partial^2F_1}{\partial y^2}+\frac{\partial^2F_1}{\partial z^2},\hspace{5pt} \frac{\partial^2F_2}{\partial x^2}+\frac{\partial^2F_2}{\partial y^2}+\frac{\partial^2F_2}{\partial z^2},\hspace{5pt} \frac{\partial^2F_3}{\partial x^2}+\frac{\partial^2F_3}{\partial y^2}+\frac{\partial^2F_3}{\partial z^2} \right)}$$

$$=\left(\nabla^2F_1,\hspace{5pt}\nabla^2F_2,\nabla^2F_3\hspace{5pt}\right)$$

ここで最後の式の各成分については∇^２F_１などはスカラー場に対してラプラス演算子が作用する形をとっています。

ベクトル場に対してラプラス演算子を作用させる場合には注意点もあります。
∇^２＝∇・∇と考える事には問題ありませんが、
例えば\(\nabla\left(\nabla\cdot\overrightarrow{F}\right)\neq(\nabla\cdot\nabla)\overrightarrow{F}\)です。

ベクトル場の発散はスカラー場になりますから、それに対してハミルトン演算子を作用させると結果は再びベクトル場になります。
しかし結果は、\(\nabla\left(\nabla\cdot\overrightarrow{F}\right)\)の例えば第１成分には「Ｆ_２をｘとｙで偏微分した関数」が生じるのです。これは∇^２\(\overrightarrow{F}\) の結果とは異なるものになっています。

この事はスカラー場に対するラプラス演算子の作用の考察において結果的には
「∇^２＝∇・（∇φ）」として扱うけれども単純に括弧を外してナブラをくっつけるのとは違うと考えられる事に関連しています。

通常のベクトルの場合でも、３つのベクトル対して
\(\overrightarrow{C}\left(\overrightarrow{A}\cdot\overrightarrow{B}\right)と\left(\overrightarrow{C}\cdot\overrightarrow{A}\right)\overrightarrow{B}\) は一般的に異なるベクトルです。
そのように、演算の結果同士で等号で結べるものとそうでないものがある事には注意が必要となります。

ナブラで作る「スカラー演算子」

最後に、ナブラ記号を使って発散を表した時の「内積の順番」を入れ換えた形の演算子についても触れておきます。これはスカラー演算子などと呼ばれる事もあります。あるベクトル場とナブラ記号が結び付いて「１つの演算子」として機能します。

$$スカラー演算子：\overrightarrow{A}\cdot\nabla（これでまとめて演算子扱い。）$$

$$\left(\nabla\cdot\overrightarrow{A}であれば\mathrm{div}\overrightarrow{A}の事\right)$$

スカラー演算子はラプラス演算子と似ていてスカラー場とベクトル場の両方に作用させる事ができます。（ラプラス演算子はスカラー演算子の１つであるという見方をする場合もあります。）

より具体的には、ハミルトン演算子（スカラー場に作用する単独の∇）との内積的な計算はしますが偏微分の操作自体はいじらず、３つの偏微分に対して１つのベクトル場の対応する成分が乗じられているというものです。例えば次のようになります。

$$\overrightarrow{A}\cdot\nabla=A_1\frac{\partial}{\partial x}+A_2\frac{\partial}{\partial y}+A_3\frac{\partial}{\partial z}$$

これをスカラー場に演算子として作用させると、別のスカラー場になります。次のようになります。

$$\left(\overrightarrow{A}\cdot\nabla\right)\phi=A_1\frac{\partial\phi}{\partial x}+A_2\frac{\partial\phi}{\partial y}+A_3\frac{\partial\phi}{\partial z}$$

ベクトル場に作用させる場合にはラプラス演算子と考え方は同じで、それぞれの成分に対して演算子が作用するという計算になります。計算結果はベクトルのままです。

$$\left(\overrightarrow{A}\cdot\nabla\right)\overrightarrow{B}=\left(A_1\frac{\partial\phi}{\partial x}+A_2\frac{\partial\phi}{\partial y}+A_3\frac{\partial\phi}{\partial z}\right)\overrightarrow{B}$$

$$=\small{\left( \frac{\partial B_1}{\partial x}+\frac{\partial B_1}{\partial y}+\frac{\partial B_1}{\partial z},\hspace{5pt} \frac{\partial B_2}{\partial x}+\frac{\partial B_2}{\partial y}+\frac{\partial B_2}{\partial z},\hspace{5pt} \frac{\partial B_3}{\partial x}+\frac{\partial B_3}{\partial y}+\frac{\partial B_3}{\partial z} \right)}$$

ラプラス演算子の時と同様に、まず３つのベクトル場ができてから合わさるという考えでも、ベクトル場の各成分にスカラー演算子が作用すると考えても結果は同じです。

このようなスカラー演算子を作用させる例としては、実は３変数関数（スカラー場としてみなせる）に対する全微分がその形を作っています。（２変数の全微分でも考え方自体は同じです。）

スカラー場を３変数のそれぞれによって偏微分し、各項にはｄｘ，ｄｙ，ｄｚが乗じられている形ですから（ｄｘ，ｄｙ，ｄｚ）というベクトルとナブラ記号を組み合わせたスカラー演算子を考えれば全微分の形になるわけです。

$$\overrightarrow{R}=(dx,dy,dz)によるスカラー演算子\overrightarrow{R}\cdot\nablaを考えると$$

$$\overrightarrow{R}\cdot\nabla=dx\frac{\partial}{\partial x}+dy\frac{\partial}{\partial y}+dz\frac{\partial}{\partial z}であり、$$

$$スカラー場の全微分d\phi=dx\frac{\partial\phi}{\partial x}+dy\frac{\partial\phi}{\partial y}+dz\frac{\partial\phi}{\partial z}=\left(\overrightarrow{R}\cdot\nabla\right)\phi$$

スカラー場に対して全微分を作る演算子をベクトル場に対して作用させた場合には各成分が全微分の形になり、これをベクトルの全微分と呼ぶ事があります。

$$同じく\overrightarrow{R}=(dx,dy,dz)によるスカラー演算子\overrightarrow{R}\cdot\nablaを考えて$$

$$ベクトル場の全微分d\overrightarrow{F}=(dF_1, dF_2,dF_3)=\left(\overrightarrow{R}\cdot\nabla\right)\overrightarrow{F}$$

$$第１成分だけ記すとdF_1=dx\frac{\partial F_1}{\partial x}+dy\frac{\partial F_1}{\partial y}+dz\frac{\partial F_1}{\partial z}$$