今回は、全微分という、少し聞きなれないかもしれない考え方について説明します。これは、前回の偏微分の理論と直接的に関係するものです。全微分の考え方を述べた後に、物理の熱力学での応用について述べます。
英名では、全微分は exact differential あるいは total differential と言います。
★ このページでは、「関数」と言ったら全て(偏)微分可能な関数の事を指す事にします。そのため、「連続な」「偏微分可能な」といった表現は基本的に省略いたします。解析学的に見る場合は、それらの考察も重要になります。
「全微分」とは何か?定義と考え方・偏微分との関係
初めに、数学的な定義と考え方です。本質的に、偏微分と深い関わりがあります。
■ 全微分の定義 単独で表れるdF、dx、・・
■ 全微分と「合成関数に対する偏微分の公式」との関係
■ 1変数の場合の dF や dx の元々の数学的意味は?
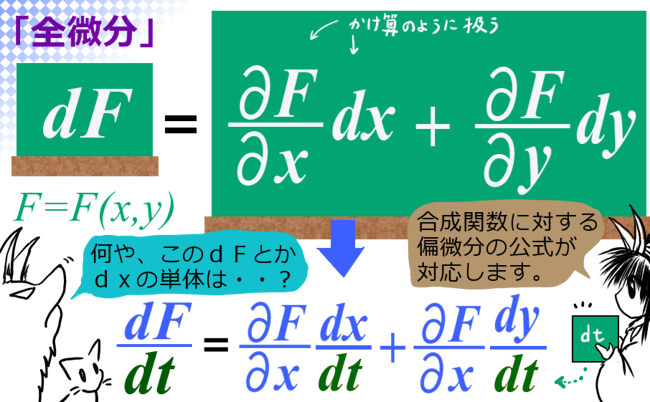
全微分の定義 単独で表れるdF、dx、・・
全微分とは多変数関数について定義されます。多変数関数に関しては偏微分を考える事ができますが、この偏微分による偏導関数を用いて全微分は定義されます。
多変数関数 F(x,y,z,・・) の全微分とは、次のように定義します。
$$dF=\frac{\partial F}{\partial x}dx+\frac{\partial F}{\partial y}dy+\frac{\partial F}{\partial z}dz+\cdots$$
このように、単独でdFというものを定義し、別の単独のdxやdyを偏微分(偏導関数)と組み合わせて定義するものが全微分です。(※単に「微分」と呼ぶ事もありますが、当サイトでは避けます。)
物理では、良く使われます。意味については後述していきましょう。
この「dF」が単独で表現される事に違和感を覚えるかもしれません。実際、このままでは具体的な関数の微分計算はできません。例えば、具体的な関数 \(F(x) =e^x\) に対して dF というものを考えたとしても、それは \(dF=d(e^x)\) とだけしか表現のしようのない物でそれ以上計算はできません。導関数として計算できるのは、あくまでdF/dxです。
では、上記定義で表される「全微分」とは何の意味があるのでしょう?この定義の計算としての意味は、じつは合成関数に対する偏微分の公式です。
全微分と「合成関数に対する偏微分の公式」との関係
全微分の定義には偏微分が含まれていますが、本質的に、偏微分について成立する公式と直接的な対応を持っています。合成関数に対する偏微分の公式は、x、y、z・・の各変数が、別の1つだけの変数の関数である場合は次のようになります。
多変数関数 F(x,y,z,・・) の各変数が別の変数t(のみ)の関数である時:
$$\frac{dF}{dt}=\frac{\partial F}{\partial x}\frac{dx}{dt}+\frac{\partial F}{\partial y}\frac{dy}{dt}+\frac{\partial F}{\partial z}\frac{dz}{dt}+\cdots$$
x、y、z、・・が、t、u、v、・・などの多変数関数になる場合は、
ここでのdF/dt、dx/dtなどは偏微分∂F/∂t、∂x/∂tなどになります。
さて、これを全微分の定義の式と見比べてみましょう。
すると、形式的には「全微分の定義」の式について「両辺をdtで割った」形を考えてみるとぴったりと偏微分の公式に一致する事が分かるでしょうか?
じつは全微分の定義にはこのような「意味」があるわけなのです。
★ これは形式的に対応するという事であり、数学的に厳密にはdxをdtで「割って(除算して)」dx/dtにするという演算は行わない事に注意してください。後述もしますが、dx/dtと書いた場合はあくまで「導関数」を指し、極限値として得られる関数です。
ですから、全微分の定義式は偏微分のほうの公式から「導出・証明されるもの」ではなく、あくまで定義になります。
多変数関数が常に合成関数として扱えるという保証はないわけですが、具体的な計算を考える時に意味を持つのは合成関数に対する偏微分の公式のほうです。
それを踏まえたうえで、多変数関数に対する全微分を考える事は割と多くあり、特に物理では使用する事が多いです。
1変数の場合の dF や dx の元々の数学的意味は?
物理などの応用で使う場合は、dF や dx という表記を単独で用いる場合は「微小量」を表す事が多いです。ただし、じつは数学の解析学的にもきちんと意味があります。
上記のように 多変数関数F(x,y,・・)に対する「全微分」dFが定義されるわけですが、じつは1変数関数F(x)に対しても同様にdFという単独の表記にも解析学での定義があります。
解析学的には、dFやdxというのは、
じつは本来は、ある点を新しい原点として設定した時の座標軸の変数です。
その新しい原点での、関数F(x)に対する接線の傾きをAとして、
dF=A(dx)
という1次式を考えます。この1次式は、近似1次式とも呼ばれます。
解析学的に厳密には、この時のdFの事を1変数関数におけるF(x)の微分と言うのです。
この意味では、接線の傾きは「割り算」によって「A=(dF)/(dx)」という事になります。
ただし、導関数として dF/dxと書く時は、あくまで極限値としての導関数として、
dF/dx という表記全体で1つの意味を持つ事にしています。
(導関数に具体的な値を代入したものを微分係数と呼ばれます。)
こういった事が、決め事として少々分かりにくいところかもしれません。
★ 数学において、特に解析学・微分積分学においてdF/dxの事を「導関数」と呼ぶ事にこだわって、慣習的な俗称である「微分」という言葉で呼ぶ事を極力避けようとする傾向があるのはこういう理由があると言えます。本来、数学の用語として区別する事に決めているものであるためです。
ただし応用ではその区別があまり重要でないため(近似的にほぼ同じものとみなせるという解釈を前提におくため)、慣習的に導関数と言わずに「微分」と言ってしまう事が多いわけです。
じつは全微分の定義とは、この意味で用いられているものなのです。すなわち、多変数関数に対しても同様に、dF=A(dx)+B(dy)+C(dz)+・・を考えるという意味です。2変数関数の場合は、3次元座標での「接平面」を考えている事になります。
★ 上記でも触れましたが、多変数の場合でも「微分」と言ってしまう場合もあります。しかしこのサイトでは、基本的に多変数の場合は「全微分」と呼ぶ事にします。
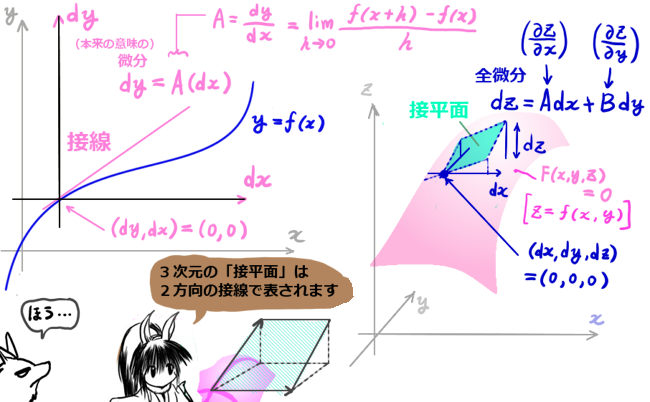
この時に、1変数関数の場合には接線の傾きと考えていたものについて、多変数関数の場合は各変数に沿った傾きとするわけです。座標上の具体的な点においては、偏導関数に特定の値を代入した偏微分係数が各傾きになります。
すなわち上の式で、A=∂F/∂x、B=∂F/∂y、C=∂F/∂z、・・という事です。
意味としては、こういう事なのです。
重要公式:積の形の関数に対する全微分
2つの多変数関数F(x,y,z,・・)と G(x,y,z,・・)の積【掛け算】FGに対する全微分d(FG)を考えてみます。結論を先に言うと、1変数の微分の時の積の微分の時と同じ形の式が成立します。これも、物理での応用で使われます。
■ 積の形の関数に対する全微分の公式
■ 証明に必要な事: 積の形の関数に対する偏微分
■ 積の形の全微分の式の証明
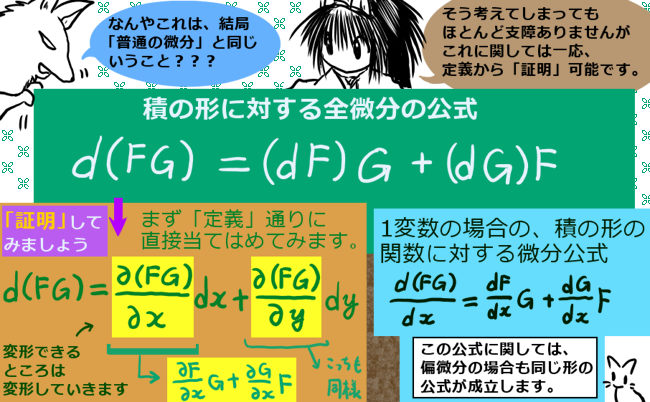
積の形の関数に対する全微分の公式
積の形の関数に対する全微分については、通常の1変数関数の場合の、積に関する微分公式同様の式が成立します。
これは数学の解析学ではそれほど重要な式ではありませんが、物理では使う事があるので述べておきましょう。
次のように、2つの項の和の形で表されます。 $$d(FG)=(dF)G+(dG)F$$ $$=\left(\frac{\partial F}{\partial x}dx+\frac{\partial F}{\partial y}dy+ \frac{\partial F}{\partial z}dz+\cdots\right)G+\left(\frac{\partial G}{\partial x}dx+\frac{\partial G}{\partial y}dy+\frac{\partial G}{\partial z}dz+\cdots \right)F$$ これは全微分の定義から導出もできますし、積の形の合成関数の偏微分公式に対応させても可です。
この公式が成立する事を示すには、「積の形の関数に対する偏微分」がどのように表されるかという事が問題になります。ただ、この問題はじつは難しくなくて、1変数の時と同じように考える事が出来ます。
証明に必要な事: 積の形の関数に対する偏微分
偏微分に関して、積の形に対する計算は通常の微分の場合と同じく次式が成立します。
$$\frac{\partial }{\partial x}(FG)= \frac{\partial F }{\partial x} G+ \frac{\partial G } {\partial x} F$$
これに対する証明は、(合成関数の場合とは違って)1変数の場合の積に対する微分公式と全く同じです。プラスマイナスでゼロになる2つの項を加える事で証明できます。式の形を見ると、本質的に1変数の時と同じである事が分かります。
2変数の場合を記しますが、何変数でも同じです。
$$ \frac{\partial }{\partial x}(F(x,y)G(x,y))= \lim_{h\to 0}\frac{F(x+h,y,)G(x+h,y)-F(x,y)G(x,y)}{h}$$
$$= \lim_{h\to 0} \frac{F(x+h,y)G(x+h,y)-F(x,y)G(x+h,y)+\{ F(x,y)G(x+h,y)- F(x,y)G(x,y)\}}{h} $$
$$= \lim_{h\to 0} G(x+h,y) \frac {F(x+h,y) – F(x,y)}{h}+ \lim_{h\to 0} F(x,y) \frac {G(x+h,y) – G(x,y)}{h}$$
$$= \frac{\partial F }{\partial x} G(x,y)+ \frac{\partial G }{\partial x} F(x,y)【証明終り】 $$
このように、1変数の時と同じです。
★ 合成関数の時に通常の微分と偏微分とで追う式の形が変わるのは、1つの変数tなどに対してx、y、z、・・の全ての変数に関して x+h, y+h, z+h,・・を考える必要があり、プラスマイナスゼロになる項を複数加える必要があるからです。
積の形の全微分の式の証明
では、関数が積の形の場合の全微分の式の「証明」について見てみましょう。
こういう場合、上記の定義のFの部分に(FG)という積の形をそのまま入れて、計算が可能であれば進めていって公式を得るという方法をとります。すると、よく見ると積の部分は偏微分の計算さえできればよい事が分かります。
積の形になっている部分の偏微分を、1変数の時と同じ要領で計算していきましょう。すると・・・・。
$$d(FG)=\frac {\partial (FG) }{\partial x}dx+ \frac {\partial (FG) }{\partial y}dy$$
$$= \left(\frac{\partial F }{\partial x} G+ \frac{\partial G }{\partial x} F\right) dx+ \left(\frac{\partial F }{\partial y} G+ \frac{\partial G }{\partial y} F\right) dy$$
$$ = \left(\frac{\partial F }{\partial x}dx + \frac{\partial F }{\partial y}dy \right)G+ \left(\frac{\partial G }{\partial x}dx + \frac{\partial G }{\partial y}dy \right)F=(dF)G+(dG)F 【証明終り】$$
このように、偏微分に関して積の計算をした後、上手にFとGに関してまとめると、dFとdGの定義の形が出てくるので d(FG)=(dF)G+(dG)F という形にまとまるわけです。
つまり、結果として、多変数関数に対する全微分も、積の形の関数に対しては
1変数関数や偏微分の場合と同じ形になる、という事です。
じつは、合成関数の偏微分に対して積の形の場合を計算して対応させると考えても同じ結果を得ます。
その場合の計算も記しておきましょう。
(上記と同じく、x,y はtだけの関数とします。つまり∂x/∂t=dx/dtです。)
$$\frac{d(FG)}{dt}=\frac {\partial (FG) }{\partial x}\frac{dx}{dt}+ \frac {\partial (FG) }{\partial y}dy$$
$$= \left(\frac{\partial F }{\partial x} G+ \frac{\partial G }{\partial x} F\right) \frac{dx}{dt} + \left(\frac{\partial F }{\partial y} G+ \frac{\partial G }{\partial y} F\right) \frac{dy}{dt} $$
$$= \left(\frac{\partial F }{\partial x} \frac{dx}{dt} + \frac{\partial F }{\partial y} \frac{dy}{dt} \right)G+ \left(\frac{\partial G }{\partial x} \frac{dx}{dt} + \frac{\partial G }{\partial y} \frac{dy}{dt} \right)F= \frac{dF}{dt} G+ \frac{dG}{dt} F $$
得られた式から形式的にdtの部分を除くと、積の形に対する全微分の式にちょうど対応します。
物理での使い方:熱力学での例
全微分の形で議論を進める分野の1つの例として、初歩的な熱力学の理論について述べます。
■ 熱力学での色々な変数
■ 内部エネルギー変化dUの計算 全微分と偏微分の関係の利用
■ エンタルピーHの変化量dH と積に対する全微分の式
この理論はさらに、化学反応に対する物理化学的な考察に使われたりします。
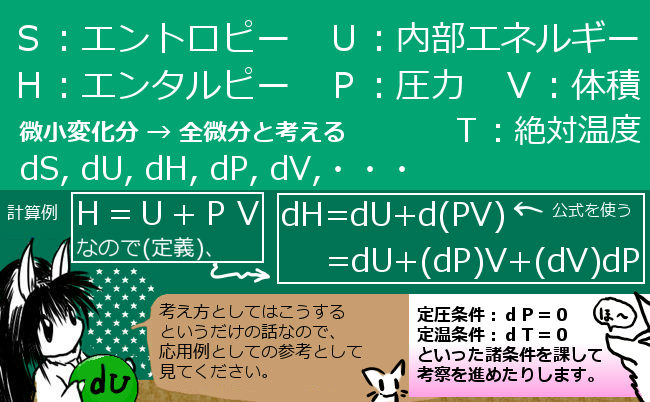
熱力学での色々な変数
熱力学とは、通常の力学や電磁気学とは少し性質が異なり、どちらかというと物理化学などの分野と相性がよい領域です。熱力学では、ある「系」(例えば容器に入った気体)について、まず次の量を考えます。
- 体積V
- 圧力P
- 温度T【これは、いわゆる絶対温度で、0[℃]を298[K]とします。】
- 内部エネルギーU
また、これらを組み合わせた量や、系に出入りする「熱」(温度とは別)も考えます。
- 熱 q
- 仕事 w【本質的には力学での仕事と同じものです。】
- エンタルピー H=U+PV【主に発熱・吸熱として観測できる量です。】
- エントロピーS ・・dS = Δq /T なるSとして定義
これらの変化量を dV 、dP などの全微分の形で表記して議論を進めます。物理でこれらを考える場合には時間という変数で微分・積分が可能と考えられますからdv/dtなどを考えても同じ事ですが、導関数ではなくて全微分の形で話を進めてしまう事が普通です。
上記の量のうち、「エントロピー」(記号S)というものだけが妙な定義のされ方をされているように見えるかと思いますが、これで計算を行うという理論になります。意味としては、系の「乱雑さ」の度合いを表す量です。
$$積分によりS=\int_{T1}^{T2 } \frac{Δq}{T} dTとも表せます。【このページでは、あまり関係ありません。】$$
「エンタルピー」という量(記号H)も少し分かりにくいかもしれませんが、定圧条件(dP=0)で dH=Δq となり、発熱・吸熱として比較的観測しやすい量なので敢えて定義されるものになります。
参考:系の「状態量」であるものは体積・圧力・温度・内部エネルギー・エントロピーであり、熱や仕事は「非状態量」です。「非状態量」という語には、系にされる仕事と形に出入りする熱の比は条件によっていくらでも変えれるので系自体の状態の量を表さない・・という意味合いが含まれています。熱力学では重要な考え方です。微小量を考える時、状態量については全微分としてdVなどで表し、非状態量についてはΔqなどと書いて区別する事が多いです。
内部エネルギー変化dUの計算 全微分と偏微分の関係の利用
まず、内部エネルギーの「変化」を考えます。つまり、Uに対してdUを考えるわけです。このdUは、全微分です。しかし最初は、上記の全微分の定義は直接的には使わずに少しだけ計算を進めます。いくらか変形した後で適用する箇所があります。
物理的な考察から、dU=Δq + Δw と書いておきます。※dw、dqと書いてもよいのですが、非状態量である事を強調して区別する事が多いです。
意味としては、外部からの圧力で仕事がされた、外部から熱が入ってきたという状況です。(あるいは膨張などで外部に仕事をした・熱が外に出て行ったなど。)
ここで、まずΔw=- (dV)P の関係があります。
これは、等圧(dp=0)の条件下で、次の仮定でのモデルを考える事によります:
- 系が外部に仕事をした時は体積が増える。
- その分、内部エネルギーは減る。(温度は下がる。)
逆に、逆に外部から仕事をされた場合は体積は減りますが内部エネルギーは増えます。
また、熱の変化Δqに関しては、
dS=Δq/T ⇔ Δq=(dS)T
の関係からエントロピーでの表記に直します。
組み合わせて、dU=(dS)T -(dV)P という関係式を作っておきます。
数学的な全微分の定義の式を直接使って考察をするのはここからです。
ここで、Uが多変数関数U(S,V,・・)であるとして、
さらに「等圧条件」dP=0と「等温条件」dT=0という場合を考えます。
(このように所定の条件を加えて考察する事が多いです。)
すると、全微分としては次のようにります。
$$dU=\frac{\partial U}{\partial S}dS+\frac{\partial U}{\partial V}dV+\frac{\partial U}{\partial T}dT+\cdots= \frac{\partial U}{\partial S}dS+\frac{\partial U}{\partial V}dV $$
普通に全微分を考える際にはdP、dTを含めた項も含まれますが、dP=0、dT=0【圧力、温度の変化は無し】という条件を設けるので式が簡単になるわけです。
成立する2式を並べて書くと次のようになります。
この事から何が言えるでしょう?
結論を言いますと、Uに対するS,Vの偏導関数がそれぞれT、Pであると解釈がなされるのです。
ここから先も計算による考察が続くのですが、このページではここで止めておきます。
エンタルピーHの変化量dH と積に対する全微分の式
次の例として、エンタルピーHの変化量dHを考えてみましょう。
これに対しては、積に対する全微分の式を用いるのです。
「エンタルピー」Hの定義は、H=U+PV です。も考えておきます。
次に、Hの変化量(全微分)を考えます。
これは dH=dU+d(PV) になります。
ここで上記の「積の形に対する全微分」の公式を適用しましょう。
PVという、圧力と体積の積になっている部分に対して適用します。すると、
dH=dU+d(PV) = dU+(dP)V+(dV)P
という形になるわけです。
参考:等圧条件dP=0の時、dH= dU+(dP)V+(dV)P = dU+(dV)Pになります。
他方、dU=Δq+Δw=Δq-(dV)Pなので、dU+ (dV)P=Δq
つまり、dP=0 ⇒ dH=Δq という事であり、
等圧条件下ではエンタルピーの変化は熱の変化(系への出入り)として表される
・・という解釈が、理論的に成立するというわけです。
前述でも触れましたように、この部分の計算は1変数関数の積に対する微分公式と同じ形になるので「通常の微分(変数は時間)」と捉えて計算しても結果的に差し支えない箇所です。
ただし、本質的にこれらのP、V、U、Sなどは多変数関数である事に注意も必要です。そのため、一応多変数関数の全微分と捉えたほうがよいとは思います。
この他に、A=U-TS、G=H-TSといった量を考えます。(いずれもエネルギーとして考えられます。)dAやdGも、dHと同じく積に関する全微分の式を考えて変形を行う事ができます。
熱力学というのは決して分かりやすい分野ではなく、この他にも色々な面倒な計算の理論があったりします。しかし、数学の偏微分や全微分の理論を踏まえておくと、初歩的な部分に関しては大分分かりやすくなるのではないかと思います。
参考文献・参考資料
■ 参考文献のリンクは、外部リンクになります。


