この記事では初等関数の微分公式とその導出・証明をまとめています。ここで扱う初等関数は主に単項式、三角関数、指数関数、対数関数を主に指します。(逆三角関数は別の記事で詳しく扱っています。)
- 初等関数の微分公式の一覧表
- 初等関数の微分公式の証明
(個々の微分公式の証明)
■ 単項式
■ e の指数関数
■ 一般の指数関数
■ 自然対数関数
■ 三角関数(正弦、余弦)
■関連サイト内記事:微分についての定義や定理、関連する事項などです。
初等関数の微分公式の一覧表
基本となる初等関数の微分公式
初等関数について、微分演算によって得られる導関数のうち、
最も基本的なものと思われるものをまとめると次のようになります。
| 関数名 | 式 | 導関数 | 備考 |
| 定数関数 | y=c | y’=0 | 定数に対する微分は0になります。 |
| 単項式 | y=xa | y’=axa-1 | aは実数で、y=1/xや y=\(\sqrt{x}\) を含む |
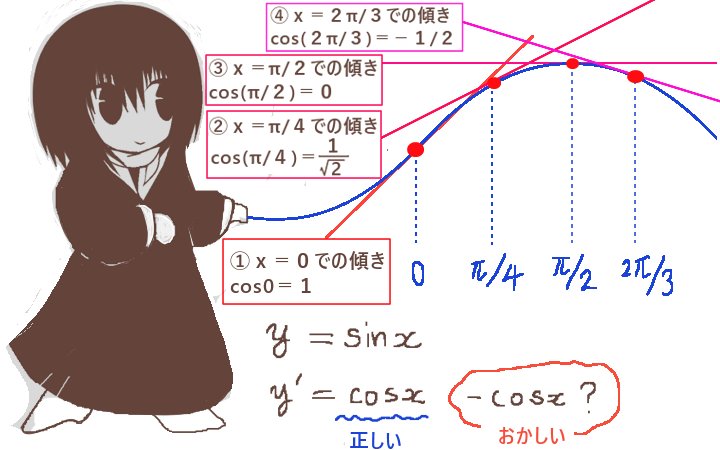
| 正弦関数 | y=sinx | y’=cosx | 4回微分するともとの式に戻る |
| 余弦関数 | y=cosx | y’=-sinx | 4回微分するともとの式に戻る |
| 指数関数 | y= ex | y’=ex | 自然対数の底 e を使った場合。 もとの関数と導関数が一致。 |
| 対数関数 | y= lnx | y’=1/x | 自然対数関数の場合。(底が e) |
「単項式」とは2次関数や3次関数がxaの形で単独で存在しているものを指し、それを定数倍と和や差で組み合わせると「多項式」になります。
定数関数については単項式で指数が0の場合と考えても可です。定数関数の微分が0になるという事は、要するに普通の1とか2とかの定数を微分すると結果は必ず0であるという意味です。
単項式の導関数について代表的なものをいくつか挙げると次のようになります。
| a | 単項式 | 導関数 | 備考 |
| a=1 | y=x | y’=1 | 2階微分は0 |
| a=2 | y=x2 | y’=2x | 2階微分は定数 |
| a=3 | y=x3 | y’=3x2 | 3次関数のグラフの 形状に関係 |
| a=-1 | y=1/x =x-1 | y’=\(-\frac{\Large 1}{\Large x^2}\) =-x-2 | x=0で微分不可能 (関数を定義できない) |
| a=-2 | y=1/(x2) =x-2 | y’=\(-\frac{\Large 2}{\Large x^3}\) =-2x-3 | x=0で微分不可能 (関数を定義できない) |
| a=1/2 | y=\(\sqrt{x}\) =x1/2 | y’=\(\frac{\Large 1}{\Large 2\sqrt{x}}\) =(1/2)x-1/2 | x=0で微分不可能 (導関数を定義できない) |
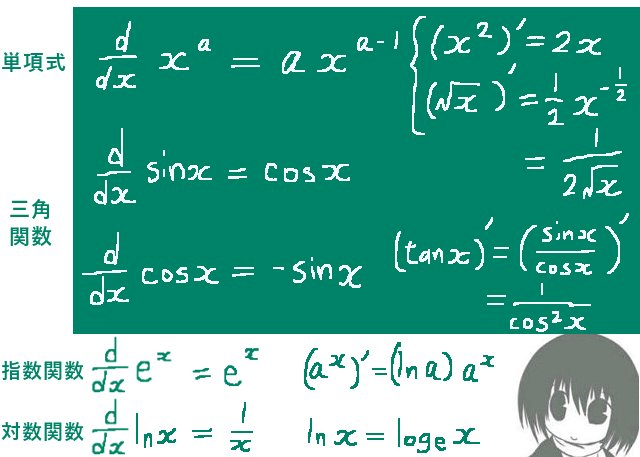
その他の初等関数の微分公式
次に、その他の初等関数の微分公式です。
これらは、基本となる微分公式から導出できるものが少なくありません。
| 関数名 | 式 | 導関数 | 備考 |
| 正接関数 | y=tanx | y’=1/(cos2x) =1+tan2x | 正弦、余弦の微分公式と 積・商の微分公式から |
| 指数関数 (一般) | y=ax | y’=(ln a)ax | e 以外の指数関数 |
| 対数関数 (一般) | y= logax =(lnx)/(ln a) | y’=1/(xln a) | e 以外の底。 底の変換公式使用 |
| 逆正弦関数 | y=Arcsinx | y’=\(\frac{\Large 1}{\Large \sqrt{1-x^2}}\) | マイナス符号をつけると 逆余弦関数の導関数 |
| 逆正接関数 | y= Arctanx | y’=\(\frac{\Large 1}{\Large 1+x^2}\) | 積分で理論上 重要な場合がある |
| 双曲線関数 | y= \(\frac{\Large e^x-e^{-1}}{\Large 2}\) =sinhx y= \(\frac{\Large e^x+e^{-1}}{\Large 2}\) =coshx | (sinhx)’=coshx (coshx)’=sinhx | 三角関数の導関数の 関係に似ている。 (微妙に違う。) |
微分の公式と接線の傾きの関係
初等関数の微分公式は、基本となる単項式・三角関数(特に正弦と余弦)・指数関数・対数関数に限って言えば比較的平易な形をしているとも言えます。
と言ってもプラスとマイナスの符号の関係など、細かい部分は混乱する事もあるかもしれません。そのような時には、関数のグラフの接線の傾きとしての微分係数を考えてみると理解に役立つ場合があります。
関数のグラフを描いてみて、接線の傾きが正(グラフで言うと右上がり)、負(右下がり)、0、無限大など、見て大体分かる部分があるので、微分の公式の導関数との対応を考えると比較的分かりやすいです。
対数関数などは、 微分して得る導関数は 1/x ですが、x がゼロに近づくにつれて無限大の急な傾きになっていく事が表現されています。また、逆に x を無限大にしていくと傾きはどんどん緩やかに0に近づいて行く事になります。
x = 0 付近で傾きが非常に急で無限大に近く、x の値が巨大になるにつれて傾きが緩やかになり次第にほとんど0になるのは、「xの平方根」(xの1/2乗)などの関数でも同じです。
初等関数の微分公式の証明
微分の定義式からの個々の関数の微分公式の導出および証明を記します。
なるべく定義式からの極限として考えますが、
積の微分公式・合成関数の微分公式・逆関数の微分公式を途中で使ったほうがよい事もあります。(積の微分公式等はいずれも微分の定義式から導出されます。)
基本となる初等関数の微分公式は結果は比較的平易ですが、単項式で実数を指数とする場合の証明は意外と複雑だったり、三角関数に対しては計算を進めるうえで加法定理が必要だったりと、微分の定義から公式を導出する過程は意外と複雑であったりします。(そのため、微分を使っていくうえでは証明方法を理解したうえで「公式の結果は覚えてしまったほうが早い」とも言えます。)
単項式の微分公式の証明
定義式に直接単項式を代入すると、$$\frac{(x+h)^a-x^a}{h}$$となります。
他方で(x+h)a について、a が自然数 nであれば2項定理で展開する事によって$$\frac{nhx^{n-1}}{h}=nx^{n-1}$$の項だけが h→0 で 残り、他の項は全てゼロに収束します。
つまりx2の導関数2xや、x3の導関数3x2における、
2とか3とかの係数は2項展開した時の係数由来(nC1の項)であるというわけです。
しかしa が自然数でない場合には、少し証明に工夫を要します。
a が実数の場合でも「一般2項定理」が成立するのですが、その肝心の一般2項定理の証明が、一般的には単項式の微分の結果を使って行われます。(マクローリン展開を使います。マクローリン展開とは、微分を利用した関数の無限級数展開です。言い換えると微分の公式を必要とする展開です。)
そこで、単項式の微分公式の証明では、強引に一般2項定理の単独での証明を試みるよりは、
実は対数関数の微分を利用するほうが簡単です。
対数の性質 ln xa=a ln x に注意して、$$\frac{d}{dx}(\ln x^a)=\frac{d}{dx}a\ln x=a\frac{d}{dx}\ln x=\frac{a}{x}$$
他方で、合成関数の微分公式を用いると同じ式を別の形で表せます。
$$\frac{d}{dx}(\ln x^a)=\frac{\large{\frac{d}{dx}(x^a)}}{\large{x^a}}$$
という事は、$$ \frac{a}{x}=\frac{\large{\frac{d}{dx}(x^a)}}{\large{x^a}} $$
$$\Leftrightarrow {\large \frac{d}{dx}(x^a)=\frac{a}{x}x^a=ax^{a-1}}【h→0】$$
指数関数の微分公式の証明
指数関数の微分は、e に関する微分公式の証明が基本になります。
証明の方法は、微分の定義式に直接関数を当てはめて計算を進める形になります。
その際に、指数と対数との関係を使って式変形をしていきます。
$${\large\frac{e^{x+h}-e^x}{h}=e^x\frac{e^h-1}{h}=e^x\frac{e^h-1}{\ln e^h}}$$
次に、eh-1=kとおきます。$$e^h-1=k\Leftrightarrow\hspace{5pt}e^h=1+k\hspace{5pt}に注意して$$
$${\large\frac{e^h-1}{\ln e^h}}=\frac{k}{\ln (1+k)}=\frac{1}{\Large{\frac{1}{k}}\large{\ln (1+k)}}$$と表す事ができて、これの分母についてさらに$$\frac{1}{k}\ln (1+k)=\ln (1+k)^{\Large{\frac{1}{k}}}$$
という、e の定義式の形を含んだ式に変形できます。
h→0 の時k→0なので k に関する極限として考えてもよく、
$$\lim_{k \to 0}(1+k)^{\Large{\frac{1}{k}}}=\lim_{k \to \infty} \left(1+\frac{1}{k}\right)^k=e$$
なので
$$\lim_{k \to 0}\frac{1}{k}\ln (1+k)=\lim_{k \to 0}\ln (1+k)^{\Large{\frac{1}{k}}}=\ln e = 1 $$ですから
$$
\lim_{h \to 0}\frac{e^{\large{x+h}}-e^x}{h}=\lim_{k \to 0}e^x\frac{k}{\ln (1+k)}
$$
$$=\lim_{k \to \infty}e^x\frac{1}{\ln (1+\large{\frac{1}{k}})^k}=e^x\frac{1}{\ln e}=e^x\frac{1}{1}=e^x$$

$$\lim_{n \to 0}(1+n)^{\Large{\frac{1}{n}}}=\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n=e$$ で定義される自然対数の底 (ネピア数)e が有限の値であるという事は、きちんと証明できます。少し面倒ではありますが自然数に関する2項定理を使って式を直接展開して、対象の式を数列として見た時に「上に有界である単調増加数列である」事を示す事で証明できます。e = 2.718・・・である事はマクローリン展開を使うと見やすいです。
一般の指数関数の微分
一般の指数関数の微分については、定義に当てはめて自然対数の底の場合と全く同様にして計算を進めます。対数の底の変換公式により次のようになる事を使います。$$\log_a\left(1+\frac{1}{h}\right)^h=\frac{\large{\ln(1+\frac{1}{h})^h}}{\ln a}$$
$$これは、h → ∞ で\hspace{5pt}\frac{1}{\ln a}\hspace{5pt}に収束します。$$
微分の定義式による計算ではこの式が分母にありますから微分により得られる導関数は次式です。$$\frac{d}{dx}a^x=a^x\ln a$$
対数関数の微分公式の証明
直接定義から計算しても証明できますし、指数関数の逆関数が対数関数なので、逆関数の微分公式を用いても証明できます。いずれの方法でも、自然対数の底 e の定義式の極限値の存在が、対数関数の微分公式でも成立の根拠となります。
以下では微分の定義式から証明してみます。
$$\frac{\ln (x+h)-\ln x}{h}=\frac{\ln \large{\frac{x+h}{x}}}{h}=\frac{\ln \left(\large{1+\frac{h}{x}}\right)}{h}$$ $$=\frac{1}{x}\frac{x}{h}\ln \left(1+\frac{h}{x}\right)=\frac{1}{x}\ln \left(1+\frac{h}{x}\right)^{\LARGE{\frac{x}{h}}}$$ $$ \rightarrow \frac{1}{x}\ln e =\frac{1}{x} 【h→0】$$
三角関数の微分公式の証明
三角関数のうち正弦関数と余弦関数の微分公式は、まず定義に当てはめて、sin(x+h) の形を三角関数の加法定理によって (sinx)(cos h) +(cosx)(sin h)の形にして計算を進めれば導出する事ができます。
ただし、計算の過程の最後で$$\lim_{h \to 0}\frac {\sin h}{h}=1$$の極限の公式が必要になります。(この公式は角度を弧度法で考えないと話が変になります。)
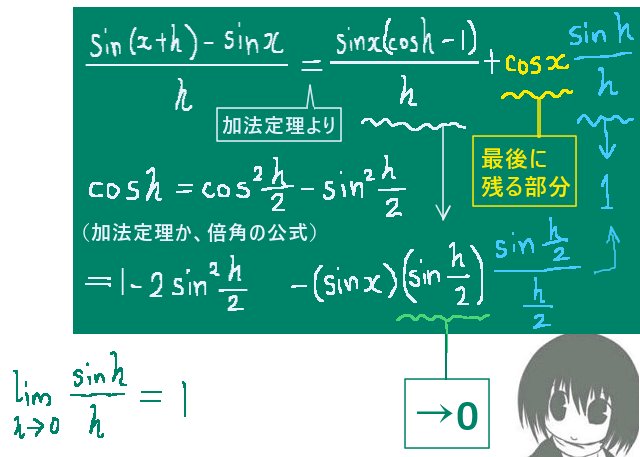
■正弦関数 sin x の微分
$$\frac{\sin (x+h)-\sin x}{h}
=\frac{\sin x \cos h + \cos x\sin h – \sin x}{h}$$
$$=\sin x \frac{(\cos h -1)}{h}+\cos x\frac{\sin h}{h}
=-2\sin x \frac{\sin^2 \Large{\frac{h}{2}}}{h}+\cos x\frac{\sin h}{h}$$
$$\left(∵ \cos h-1=\cos^2\frac{h}{2}-\sin^2\frac{h}{2}-1=1-2\sin^2\frac{h}{2}-1=-2\sin^2\frac{h}{2}\right)$$
$$=-(\sin x) \sin \frac{h}{2}\frac{\sin \large{\frac{h}{2}}}{ \large{\frac{h}{2}}}+\cos x\frac{\sin h}{h}$$
$$ →\cos x【h→0】\left(\lim_{h\to 0}\frac{\sin h}{h}=1より\right)$$
■余弦関数 cos x の微分
$$\frac{\cos (x+h)-\cos x}{h}
=\frac{\cos x \cos h – \sin x\sin h – \cos x}{h}$$
$$=\cos x \frac{(\cos h -1)}{h}-\sin x\frac{\sin h}{h}=-2\cos x \frac{\sin^2 \Large{\frac{h}{2}}}{h}-\sin x\frac{\sin h}{h}$$
$$\left(∵正弦の時と同じく \cos h-1=-2\sin^2\frac{h}{2}\right)$$
$$=-(\cos x) \sin \frac{h}{2}\frac{\sin \large{\frac{h}{2}}}{ \large{\frac{h}{2}}}-\sin x\frac{\sin h}{h}$$
$$→-\sin x 【h→0】$$
正接関数の微分に関しては定義からも計算できますが、商の微分公式を使うほうがじつは簡単です。tanx=(sinx)/(cosx) である事を利用します。
途中式にある(cosh -1)/hの極限計算は加法定理を使わない計算方法もあります。
$$\frac{\cos h-1}{h}=\frac{(\cos h-1)(\cos h+1)}{h(\cos h+1)}=\frac{\cos^2 h-1}{h(\cos h+1)}$$
$$=\frac{-\sin^2 h}{h(\cos h+1)}=\frac{-\sin h}{\cos h+1}\cdot\frac{\sin h}{h}\rightarrow 0\cdot 1=0【h\rightarrow 0】$$
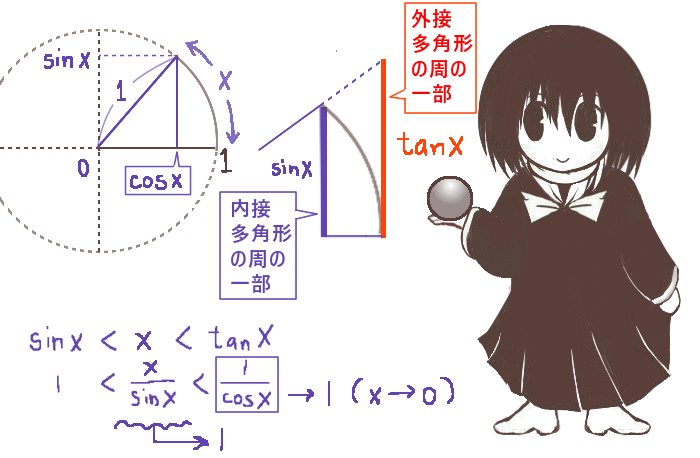
(sin x)/x の極限問題
ここでは、円弧の長さを変数とする関数として正弦、余弦、正接を考えてみます。(それが弧度法の考え方そのものでもありますが、ここでは「角度」という語を使わないで考えてみます。)
その場合に余弦と正弦波は単位円の円周上の点のx座標とy座標として考える事ができますが、正接も相似な三角形の辺の比から tanx=(sinx)/(cosx) としてきちんと考える事ができます。
この時に円弧の長さをxとすると sinx<x<tanxが成立しますが、
より詳しく見るとsinxは単位円に内接する正多角形の周の一部であり、
tanxは単位円に外接する正多角形の周の一部です。
この図形的な長さの関係は、円弧および円周の長さを計算する時に使うものと実は本質的に同じです。
すなわち円の内接多角形と外接多角形の周の長さを考えて、角の数を増やした時の極限値として円弧や円周の長さを計算するやり方です。
それらの正多角形を正n角形として考えた時、
内接する正n角形については周の長さはnについての単調増加数列となり、逆に
外接する正n角形については周の長さはnについての単調減少数列となります。
それらのn→∞の時の極限値として円弧の長さxが存在します。
詳しく言えばそれは半径および直径に比例し、円周全体の場合の比例定数はπ(円周率)です。
そのため、任意の長さの円弧についてsinx<x<tanxが成立するというわけです。
(この図形的考察は、より詳細には三角不等式等を使って丁寧に見て行く必要があります。)
この時に内接・外接する正多角形の隣り合う頂点を結んだ円弧の長さxは、x→0となります。それが(sinx)/xの極限としてx→0を考える図形的な意味です。
sinx<x<tanxに1/(sinx)を乗じると、1<x/(sinx)<1/(cosx) です。
x→0で1/(cosx)→1なので、極限の性質によりx→0でx/(sinx)→1
(sinx)/xの極限はその逆数ですが、1の逆数なのでそのまま同じ1になります。
そのため、x→0で(sinx)/x→1という事になります。