最も簡単な微分方程式５つ

大学の微積分学の入門として、簡単に解ける微分方程式について説明します。

微分方程式の解き方の手短な説明

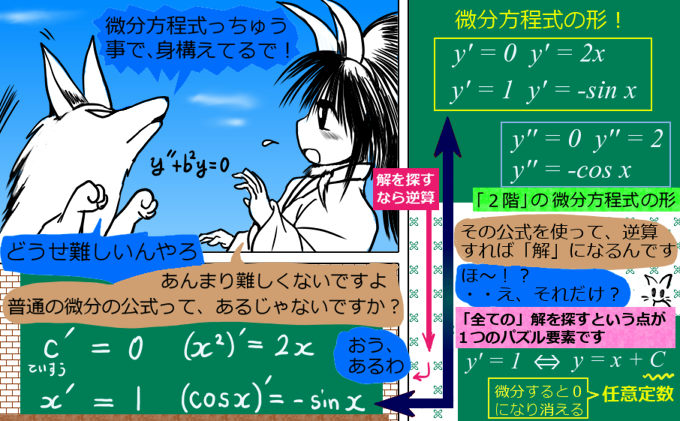
微分方程式とはその通り、微分（および高階微分）を含んだ方程式ですが、要はその方程式を満たす「関数」を探す事が、その方程式を解くという事です。このページで紹介する微分方程式は、パズル感覚で色々組み合わせるだけで解けます。

声優担当：ステ♪様　http://sute.tabigeinin.com/

つまり、微分の公式を微分方程式に当てはめてみて、確かに解になっていればよいわけです。微分の公式と言ってもたくさんあるわけですが、今回用いるのは６つで、三角関数に関しては正弦か余弦のどちらか片方あれば足りるので、実質「５つ」だけの公式を用います。それらは次の表にまとめてあります。これらを単独で使うか上手に組み合わせるかして、微分方程式を解いていけるのです。

使う公式は、この場で表にして記しておきましょう。

対象の関数	微分公式	微分方程式の解法での役割
①定数（定数関数）	\({\large \frac{d}{dx}c=0}\)	微分すると０になる
②単項式「x の a 乗」	\({\large \frac{d}{dx}x^a=ax^{a-1}}\)	微分するとx の指数が１下がる
③自然対数の底 e の指数関数	\({\large \frac{d}{dx}e^x=e^x}\)	微分すると元の関数に戻る
④-1 三角関数（正弦関数）	\({\large \frac{d}{dx}\sin x=\cos x}\)	微分2回で元の関数の符号±入替
④-2 三角関数（余弦関数）	\({\large \frac{d}{dx}\cos x=-\sin x}\)	微分2回で元の関数の符号±入替
⑤合成関数の微分	\({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\)	微分方程式内の定数倍などを調整

では具体的な微分方程式を見てみましょう。とても簡単に、解けます。

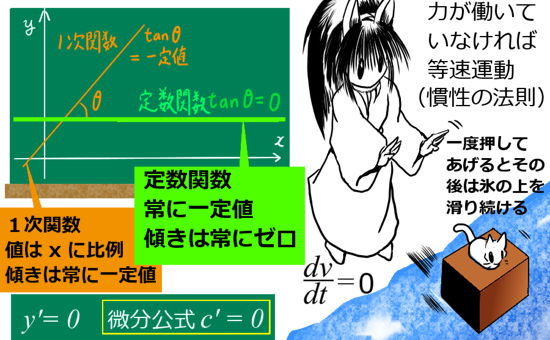
①一番簡単な微分方程式「１階微分＝０」f ‘(x)=0

最初に見るのは、「１階微分（通常微分）がゼロになる」という微分方程式です。これは、即刻解けます。しかも、運動方程式において物理的な意味も持ちます。

当てはまるような公式を探してみますと、

対象の関数	微分公式	微分方程式の解法での役割
①定数（定数関数）	\({\large \frac{d}{dx}c=0}\)	微分すると０になる

と、いうものがありますね。
定数は微分するとゼロですから、そのまま当てはまります。これで「解けた」という事になります。

１つだけ注意していただきたいのは、０や１や２などの「特定の定数」だけではなく、定数であればどんなものでもよいという事です。その事を表現するために、「任意の定数」という表現を用います。この表現は、他のタイプの微分方程式の解でも用います。
【f(0) = 1 などの具体的な x の値での関数値が条件としてあるなら、解は f(x) = 1 というただ１つの関数に定まります。そのような条件は「初期値条件」と呼ばれ、微分方程式論全体で重要です。】

物理の力学での運動方程式ではこのタイプの微分方程式は慣性の法則のうち等速運動である事を表現します。

②　２階微分＝ゼロ f ”(x)=0 １次関数　

２階微分が０になるという微分方程式も、簡単に解けるタイプのものです。高階の微分が入っていると一見難しく見えるかもしれませんが、これもじつは非常に簡単なのです。
物理的には、力が働いていない物体は等速「直線」運動する事に関わります。

２階微分が入っているので、一見、どうすればよいのか迷うかもしれません。

しかし、要するに２回微分すると０ですから・・
「１回だけの微分は『定数』」であるはず？？・・という事に気付くと、解けます。
つまり「１回の微分で定数になる関数（もう１回微分で０）」→ １次関数が解　というわけです。
使う公式としては、「１階微分＝０」の時と同じ公式の組み合わせという事に、なります。

対象の関数	微分公式	微分方程式の解法での役割
①定数（定数関数）	\({\large \frac{d}{dx}c=0}\)	微分すると０になる
②単項式「x の a 乗」	\({\large \frac{d}{dx}x^a=ax^{a-1}}\) \({\large \frac{d}{dx}x=1\cdot x^{0}=1}\)	微分するとx の指数が１下がる 「x の 0 乗」は定数

実際に、解となるはずである１次関数を「２回」微分してみましょう。

1. 微分１回目：\(\frac{d}{dx}(bx+c)=b\)（定数）
2. 微分２回目：\(\frac{d}{dx}b=0\)（ゼロ）→ ＯＫ
3. 合わせると：\(\frac{d^2}{dx^2}(bx+c)=0\hspace{10pt}\rightarrow \frac{d^2}{dx^2}f(x)=0\hspace{5pt}の解\)

というわけで、確かに１次関数 bx + c は、２階微分＝０という微分方程式の解です。
尚、定数関数も何回微分してもゼロになるので解ですが、これは１次関数で b = 0 の場合と見なせるので、任意定数 b の値に制限を設けなければ１次関数に含める事ができます。

この解の導出過程では、「１階微分＝（ゼロ以外の）定数」というタイプの微分方程式の解も、合わせて見つけている事になります。また、同じ論法を使うと、３階微分＝０、４階微分＝０といった微分方程式の解も同様に考える事が可能というわけです。
$$\frac{d^3}{dx^3}f(x)=0 の解は「２次関数」$$

$$\frac{d^n}{dx^n}f(x)=0 の解は「(n-1)次関数」$$といった感じになるのです。

それでは次に、物理的には放物運動（２次関数のグラフの形）を表す微分方程式を見てみましょう。これについては高校の物理でも多分扱われていると思いますが、微分方程式の観点から考察してみましょう。

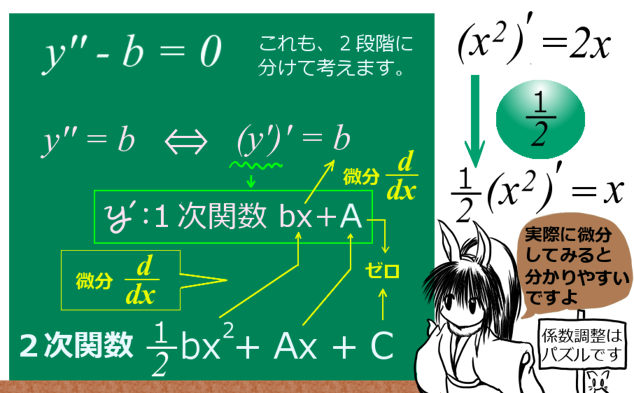
③ \(y^{\prime\prime}-b=0\)・・２次関数

「２階微分が定数に等しい」という微分方程式です。（もちろん\(y^{\prime\prime}=b\)と書いても同じです。b = 0 の場合は２階微分＝０のタイプですから、b≠0 と考えてください。）
物理的には運動方程式において地上で物を投げた時の運動としての意味があり、放物軌道の運動を表します。

■ 数学的な解法　■ 物理的な意味・・地上での水平投射の重力による運動（放物運動）

解法：１回微分すると１次関数→２回微分すると定数　と考えよう

この３つ目のタイプの微分方程式の場合、２回微分すると定数・・という事ですから、「１回微分すると１次関数」を見つければよいのです。

対象の関数	微分公式	微分方程式の解法での役割
①定数（定数関数）	\({\large \frac{d}{dx}c=0}\)	微分すると０になる
②単項式「x の a 乗」	\({\large \frac{d}{dx}x^a=ax^{a-1}}\) \({\large \frac{d}{dx}x=1\cdot x^{0}=1}\) \({\large \frac{d}{dx}x^2=2x}\)	微分するとx の指数が１下がる 「x の 0 乗」は定数

単項式の微分公式を見ると、１回微分するごとに指数（ｘの「〇乗」の〇）が１下がりますから、２次関数を１回微分すると１次関数になりますね。

ですから、解となる関数は「２次関数」です。
最後に定数 b が残ってほしいのと、係数調整のために、
\(\frac{b}{2}x^2+Ax+C\)のような形のものを選びます。２次関数の中の Ax + C の部分は、２回の微分操作の過程で０になって消えてしまうので、A と C は任意定数という形になります。
２次式を微分するために\(\frac{1}{2}\)というオマケがくっつく事に注意する必要がある事を除けば、これも難しくないのではないと思います。

実際に微分して確かめてみよう

実際に微分をしてみて、確かめてみましょう。

1. 微分１回目：
   \(\frac{d}{dx}\left(\frac{b}{2}x^2+Ax+C\right)=2\cdot \frac{b}{2}x+A=bx+A\) （１次関数）
2. 微分２回目：
   \(\frac{d}{dx}(bx+A)=b\)（定数で、しかも b に一致）→ ＯＫ
3. 合わせると：
   \(\frac{d^2}{dx^2}\left(\frac{b}{2}x^2+Ax+C\right)=b\hspace{10pt}\rightarrow ２次関数\frac{b}{2}x^2+Ax+C は、確かに\frac{d^2}{dx^2}f(x)-b=0\hspace{5pt}の解\)

物理的には、運動方程式においては「地上で物を投げた時」の運動を表します。座標同士の関係を表す軌道が２次関数の関係式になるので、放物線を描きます。

物理的意味：地上での水平投射　重力だけが働く場合は放物運動

ここでは、運動方程式で働く力が「重力」であるとします。これは、地球上では物体の質量が定まれば一意的に決まり、その大きさは mg (≒9.8m) である事が知られています。この時、水平に物を投げる（「投射する」）と、軌道は２次関数のグラフである放物線になる事を見ましょう。

■ ①考え方・・水平方向と垂直方向に分ける　■ ②設定をして、２方向の２本の運動方程式を作ろう
■ ③運動方程式の解から軌道の関係式を作ると、２次関数つまり「放物線」が得られる

① 考え方・・水平方向と垂直方向に力の働き方を分ける

水平に物を投げる（投射する）運動を考えます。投げた瞬間には力が働いているかもしれませんが、一旦手などを離れたら、水平方向には力は働かず、地面に向かう方向にのみ重力が働くと考えて数式を組み合わせるのです。

• 地面に対して水平（平行）な向き：力は働かない
  　 →　等速で運動（射影して見れば直線運動でもある）
• 地面に対して垂直（直角）な向き：重力 mg [N] が地面に向かう向きで働く
  　 →　どういう挙動をするか？（運動方程式を立てて解くと「時間の２次関数」になる）

上記の「２階微分＝０」の微分方程式の物理的意味の項目で、平面や空間の運動で運動方程式を考える場合は、力を分解して「座標成分ごとに運動方程式を立てる」という事を述べました。ここでも、同じ考え方をします。

この場合は、３次元で考えてもよいのですが、最初に物を放り投げた方向に向かって上手に１つの座標軸を合わせたと考えると、すなわち平面で考えても全く同じ運動を表せます。

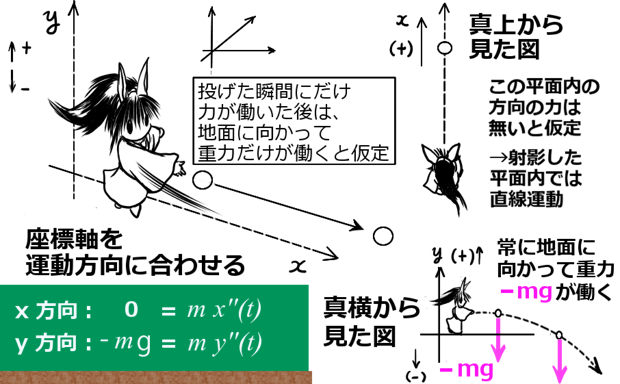
（※働く力が重力だけであると想定するので、「水平方向には力は働かない」＝「水平方向だけで見れば等速直線運動」という事が保障されるので、そのように考えてよいわけです。「直線」という事については、地面の真上から見れば「直線」になっているという事です。このような見方を「射影（しゃえい）」と言います。）

② 設定をして、２方向の２本の運動方程式を作る

このようにして考える時、どちら向きがプラスでどちら向きがマイナスかも含めて、座標軸の向きの設定を行ってから運動方程式を立てます。今、運動は平面で考える事にして、座標軸は x 軸と y 軸であるとします。

そして、２本の運動方程式を立てましょう。※尚、この場合に仮に３本目を立てたとしても、その向きには働く力はゼロ、位置もゼロから動かないので 0 = 0 という式ができるだけです。

1. x 軸成分： \(0=m\frac{d^2x(t)}{dt^2}\) → 「２階微分＝０」なので、解は t の１次関数ですね
2. ｙ軸成分：\(-mg=m\frac{d^2y(t)}{dt^2}\hspace{5pt}\Leftrightarrow \hspace{5pt}-g=\frac{d^2y(t)}{dt^2} \) → 「２階微分＝定数」の微分方程式で、
   解は t の２次関数というわけです。
   この場合、質量 m は上手い具合に両辺に入っているので、両辺で割って消せます。

y 軸成分の運動方程式で「力」の部分を – mg としているのは、空 → 地面方向は「マイナス」向きと設定したためです。地面方向に向かう「重力」の符号もマイナスにするのです。
（※では、もし「地面向き方向をプラスに設定したら + mg にするのか？」と言うと、その通りです。その場合は \(mg=m\frac{d^2y(t)}{dt^2} \)になります。符号が変わっても、解が２次関数という事自体は変わりません。）

② 運動方程式の解から軌道の関係式を作ると、２次関数つまり「放物線」が得られる

という事は、$$x(t)=bt+c,\hspace{5pt}y(t)=-\frac{g}{2}t^2+Bt+C $$という形の２式が、微分方程式である運動方程式の解として、出てくるわけです。
x(t) のほうが１次式ですから、これを t = ・・の形にして y(t) のほうの t に代入すると、$$y(x) = -Ax^2+Px+Q \hspace{5pt}(A > 0)$$ という、x に関する２次関数の形になる事が分かります。

これで、軌道が確かに「放物線」である事が表現されたわけですが、座標軸の正負の向きの設定などから、上記の各定数について b ＞ 0 、A ＞ 0 となるので、最後の結果で \(-Ax^2\)（例えば \(– 2x^2\)）という形が出てくるという事は、きちんと「下に落ちていく」という事も表しています。
このような時に結果を考察すると何だか変な事になる場合は、符号の設定などを間違えているかの可能性があるわけです。

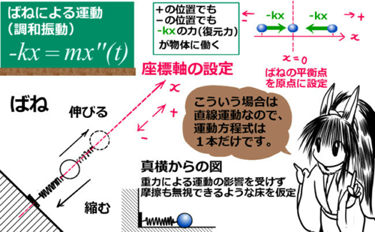
さて次は、三角関数が解になるタイプの微分方程式です。じつは、これは物理の力学で言うと「ばねの運動」なので、空間でも平面でもなく、「一次元（直線運動）」と考えてよいパターンです。ですから運動方程式は１つだけ作ればよいので、意外と考察しやすいかもしれません。

④ \(y^{\prime\prime}+b^2y=0\)・・調和振動（単振動）

このタイプの微分方程式は、２階微分と「元の関数」が入っていて、定数倍の関係にあるというものです。三角関数が関係し、物理的には抵抗力などが無い場合の「ばねの運動」（調和振動、単振動とも言います）を表します。
※\(b^2\) という「２乗」の形は、これ自体は「正の数」である事を言っています。
\(y^{\prime\prime}=-b^2y\) つまり「２階微分」＝「負の定数」×「もとの関数」という事です。

■ 数学的解法　■ 物理的な意味：ばねの運動は三角関数（調和振動、単振動）

数学的解法：まず「２回微分すると元の関数の定数倍」になる関数は？

「２回微分するともとの関数の『マイナスの定数倍』」というものは、微分公式にあるでしょうか？三角関数は、これに似ています。実際、これをパーツとして使えるのです。この時、正弦でも余弦でも同じ事なので、ここでは余弦 cos x を、使います。

対象の関数	微分公式	微分方程式の解法での役割
④-1 三角関数（正弦関数）	\({\large \frac{d}{dx}\sin x=\cos x}\)	微分2回で元の関数の符号±入替
④-2 三角関数（余弦関数）	\({\large \frac{d}{dx}\cos x=-\sin x}\)	微分2回で元の関数の符号±入替
⑤合成関数の微分	\({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\)	微分方程式内の定数倍などを調整

三角関数を２回微分すると、もとの関数の「マイナス倍」になります。
他方、解きたい微分方程式は、「『マイナスの定数』倍」となっています。
すると、符号はよいとして、微分した時だけ「定数倍」を新たに出すにはどうすればいいでしょう?

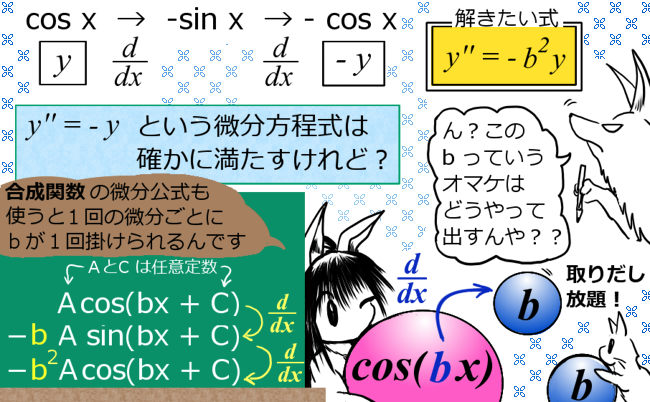
そのためには、じつは合成関数の微分公式を考えればよいのです。この考え方は、このページで紹介するタイプ以外の微分方程式でも有効な手段です。

例えば cos(2x) の微分を１階と２階について見ますと、$$１階微分：\frac{d}{dx}\cos (2x)=(2x)^{\prime}(-\sin (2x))=-2\sin (2x)$$ $$２階微分：\frac{d^2}{dx^2}\cos (2x)=\frac{d}{dx}(-2\sin (2x))=-4\cos (2x)$$ になります。y = 2x , cos(2x) = cos y と考える事ができるので、合成関数の微分公式が適用できるのです。係数として「２」というのが掛けられていますが、それが合成関数の微分由来で出てくる係数というわけです。

・・すると、この cos (2x) という関数は、２回微分するともとの関数 cos (2x) の – 4 倍になっているので、 「２回微分するともとの関数の『マイナスの定数倍』」 の条件を満たす関数の仲間である事が分かります。

という事は、定数倍として\(-b^2\)がほしいのであれば、
cos (bx) という関数を考えれば、２回微分すると合成関数の微分公式が２回適用されるので、\(-b^2\cos (bx)\)が得られます。これが解という事になりそうですね！

任意定数については、まず A を任意定数として、A cos(bx) という形でも解として成立するのです。また、別の任意定数 C を用いて Acos(bx+C) という形でも、じつはＯＫなのです。これは、合成関数の微分を行う時に、bx + C を x で微分すると b は生き残りますが C はゼロになって消えるためです。

実際に微分して確かめてみよう！

つまり、総合すると Acos (bx+C) という関数が、解になるという事です。正弦で考えても同様の形になります。実際に微分してみて、確かめてみましょう。

1. 微分１回目：\(\frac{d}{dx}A\cos (bx+C)=-bA\sin(bx+C)\)（マイナスの正弦）
2. 微分２回目：\(\frac{d}{dx}\{-bA\sin(bx+C)\}=-b^2A\cos (bx+C)\)
   （もとの関数の「マイナスｂの２乗」倍）→ ＯＫ
3. 合わせると：
   \(\frac{d^2}{dx^2}A\cos (bx+C)=-b^2A\cos (bx+C)\hspace{5pt}\Leftrightarrow\hspace{5pt}\frac{d^2}{dx^2}A\cos (bx+C)+b^2A\cos (bx+C)=0\)
   \(\rightarrow A\cos (bx+C)は、確かに\frac{d^2}{dx^2}f(x)+b^2f(x)=0\hspace{5pt}の解\)

物理的には、運動方程式を考えると、このタイプの微分方程式は「ばねの運動」を表します。ばねというと、いかにも人工的な響きがありますが、別に工学だけで用いるというものでもありません。例えば、ミクロの領域での分子の振動などを、ばねと同じタイプの振動（調和振動）と考えるモデルをもとにして考察する事が、量子力学や量子化学でもなされるのです。

物理的意味：ばねの運動は三角関数（調和振動、単振動）

運動方程式で、ばねにつながれた物体の運動を考えると、上記の「２階微分＝負の定数×もとの関数」という微分方程式になります。ばねは、抵抗力が働かないなら伸びたり縮んだりを繰り返しますから、周期関数である三角関数が解であるという事はその事実と調和しているというわけです。

■ ①まずは設定をしよう・・一次元の運動として扱えます　■ ②解いてみて完成・・結果は三角関数です

① まずは設定をしよう

抵抗力がない状態で、ばねの伸び縮みの力だけで、ばねにつながれた物体が（振動）運動しているとします。この場合は、１次元の直線運動と考えてよいので、運動方程式を３つ・２つ立てる必要はなく、１つでよいのです。ですから、式さえ立てれば、結構分かりやすいと思います。

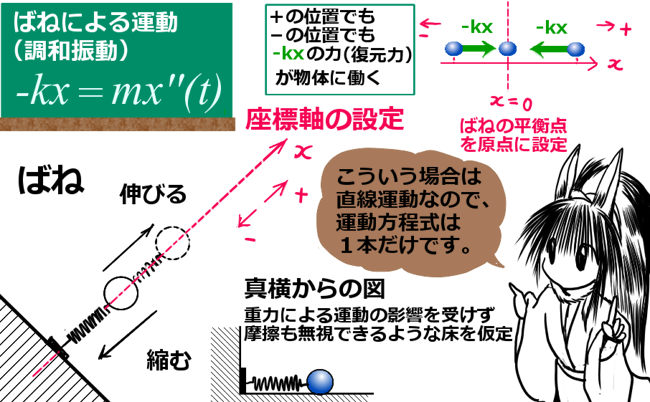
ばねの力の大きさは、ばねの「伸び」または「縮み」に比例します。（「フックの法則」と言います。）
これはつまり、ばねの平衡点（伸び縮みのない自然な状態のばねの先端の位置）から見て「位置座標」に比例するという力であるわけです。時間を変数とした場合、これは「もとの関数 x(t) 」に比例する力、というわけです。
比例するという事は比例定数もあって、「kx」という形の力が働くというわけです。この k を「ばね定数」という、そのまんまの名称で呼びます。（※物としてバネが対象ではなく、分子の振動などを調和振動モデルとして考える場合などは、「力の定数」という呼び方もします。）

ただ、プラスマイナスの符号にだけは注意しましょう。まず、ばね定数 k は正の値であるとします。次にばねの平衡点を原点 x = 0 として、座標の正負の向きを次のように設定します。

• 原点から見て、ばねが伸びている方向：プラス方向
• 原点から見て、ばねが伸びている方向：マイナス方向

この時、ばねによる力の向きを考えてみます。符号に注意してください。

• ばねが伸びている時・・つまり位置座標が正の値の時：
  力は原点向き　つまり負の方向（例えば x = 2 だったら、F = -2k ）
• ばねが縮んでいる時・・つまり位置座標が負の値の時：
  力は原点向き　つまり正の方向（例えば x = -2 だったら、F = +2k ）

これをまとめますと、「ばねの力は位置座標と常に逆の符号」という事です。 $$ばねの力：F = -kx(t)\hspace{10pt}（x(t)：位置座標、ばね定数 k>0）$$ そうしますと運動方程式は次のようになるわけです。 $$-kx(t)=m\frac{d^2x(t)}{dt^2}\hspace{10pt}\Leftrightarrow \hspace{10pt}\frac{d^2x(t)}{dt^2}+\frac{k}{m}x(t)=0$$

物体の運動の様子を調べるにはこれを解けばよいわけですが、もう分かっているわけです！

② 解いてみて完成

ばねにつながれた物体に関する運動方程式\(\frac{d^2x(t)}{dt^2}+\frac{k}{m}x(t)=0\) は、
形としては「２階微分＝負の定数×もとの関数」ですから、解は三角関数 Acos(bt+C) の形ですね。
（一応、\(\frac{k}{m}>0\)という符号にも注意してください。）

もう少し物理的に見通しをよくするために、
\(\frac{k}{m}=\omega^2\)（\(\omega\)：「オメガ」）という置き換えが、よく行われます。
そのように置き換えると、運動方程式は\(\frac{d^2x(t)}{dt^2}+\omega^2 x(t)=0\) となりますから、
解は \(A\cos (\omega t+C)\) という形で書けるわけです。

このオメガ \(\omega\) という記号は、ばねの調和振動に限らず、回転運動などの周期的な運動における角速度、角振動数、角周波数（１秒間に何ラジアン回るか）を表します。ばねの場合は「振動」ですので、角振動数と言う場合が多いです。いずれにしても、ばねの運動を周期運動と見た場合に、角度の部分（「位相」）がどのように変化するかを表す値というわけです。

ここでは \(\frac{k}{m}=\omega^2\) と、おいただけでしたから、そのような角振動数は、物体の質量とばねの性質（ばね定数の大きさの違い）によって決まるという事も分かります。

さて、使用する実質５つの公式のうち、まだ使っていないのが 自然対数の底 e の指数関数の微分公式です。最後に紹介するタイプの微分方程式は、この e の指数関数の微分公式を用いて解けます。

⑤ \(y^{\prime\prime}+by^{\prime}+x=0\)・・粘性抵抗ありのばねの運動

５つ目の微分方程式として、\(y^{\prime\prime}+by^{\prime}+x=0\) で「『特性方程式』が異なる２つの実数解を持つ場合」を説明いたします。この、後のほうにくっついてる妙な条件は別になくてもきちんと微分方程式は解けるのですが（特性方程式を使った一般の場合の解法）、簡単なのがこの条件の場合ですので、この場合を述べます。
物理的には、粘性の強い流体の中でのばねの運動で、振動する事なく少し動いて止まってしまう・・という運動を表します。

■ 数学的解法　■ 物理的意味：粘性抵抗が「強い」場合のばねの挙動

数学的解法：e の指数関数の微分を使おう

これの説明は他のものと比べて少し長いですが、「公式を上手に当てはめれば解ける」という事には変わりありません。

このタイプの微分方程式を解くには、e の指数関数の性質と、１つ前の微分方程式の例でも用いた
「合成関数の微分公式で『定数調節』」する手法を上手に組み合わせればよいのです。

対象の関数	微分公式	微分方程式の解法での役割
③自然対数の底 e の指数関数	\({\large \frac{d}{dx}e^x=e^x}\)	微分すると元の関数に戻る
⑤合成関数の微分	\({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\)	微分方程式内の定数倍などを調整

考え方を簡単に述べましょう。三角関数で cos (bx) 等を考えた時は、
１階微分で b倍、２階微分で\(b^2\)倍という定数倍調整に利用できました。
同様に、指数関数についても、定数 \(\alpha\) を用いて \(e^{\alpha x}\) といった形の関数を考えると定数倍調整に使えます。

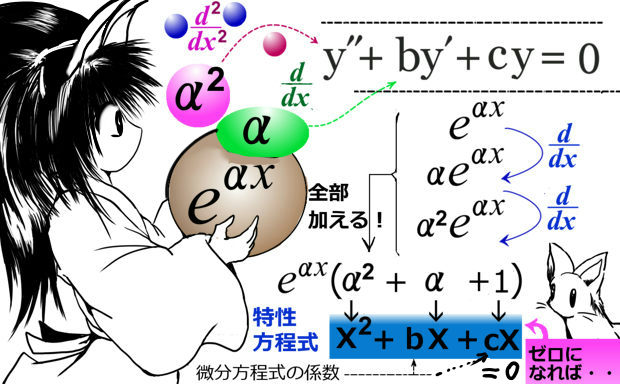
この \(e^{\alpha x}\) という関数を微分すると、

• 微分してないもとの関数：\(e^{\alpha x}\)
• 微分１回目：\(\frac{d}{dx}e^{\alpha x}=\alpha e^{\alpha x}\)
• 微分２回目：\(\frac{d^2}{dx^2}e^{\alpha x}=\alpha^2 e^{\alpha x}\)

ポイントは、「これらを加え合わせてみる」という事です。
e の指数関数は微分しても元の関数になるだけという際立った性質があるため、何回微分したとしても\(e^{\alpha x}\) が必ず含まれる事に注意して、足し算してみましょう。すると・・ $$\frac{d^2}{dx^2}e^{\alpha x}+\frac{d}{dx}e^{\alpha x}+e^{\alpha x} =\alpha^2 e^{\alpha x}+\alpha e^{\alpha x}+e^{\alpha x} =e^{\alpha x}(\alpha^2+\alpha +1)$$ もし「これがゼロ」であるなら、指数関数はゼロになりませんので、
後ろにくっついている \(\alpha^2+\alpha +1\) がゼロという事です。
少し、２次関数、２次方程式との関係がありそうですね？

では今度は、定数倍も考えて、
\(\frac{d^2}{dx^2}e^{\alpha x}+b\frac{d}{dx}e^{\alpha x}+ce^{\alpha x}\) を考えてみましょうか。 $$\frac{d^2}{dx^2}e^{\alpha x}+b\frac{d}{dx}e^{\alpha x}+ce^{\alpha x} =\alpha^2 e^{\alpha x}+b\alpha e^{\alpha x}+ce^{\alpha x} =e^{\alpha x}(\alpha^2+b\alpha +c)$$ これがゼロになるには、先ほどと同じ論法で、
\(\alpha^2+b\alpha +c=0\)となる \(\alpha\) であればよい、という事です。

\(\alpha\) が \(\alpha^2+b\alpha +c=0\) となる事を、 全く同じ意味で、次のようにも言い換えられます。 $$「\alpha が x^2+bx +c=0 の解である」$$

そしてそのような場合、じつはまさしく上の微分方程式の形：
\(\frac{d^2}{dx^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0\)を満たしています。
ですから、まず次の事が言えます。

さて、\(\alpha が x^2+bx +c=0\) の「実数解」である時で、重解では無い時、
同じく実数解となる \(\beta\) が存在するわけで、これを用いた
\(e^{\beta x}\) も、同じく\(\frac{d^2}{dx^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0\)の解なのです。
微分の基本的な性質として\(\frac{d}{dx}(bf(x)+cg(x))=b\frac{df(x)}{dx}+c\frac{dg(x)}{dx}\) というもの（線型性）があった事に注意しますと、
「特性方程式」が２つの異なる実数解を持つ時の上記の微分方程式の解は、任意定数も考慮すると次のように表せるわけです：

物理でも、運動方程式がこのタイプの微分方程式になる事があります。それについて、見てみましょう。

物理的意味：粘性抵抗が「強い」場合のばねの挙動

ばねにつながれた物体の運動を表す運動方程式には、位置座標（１次元・直線）の「２階微分」と、「もとの関数の定数（ばね定数）倍」という項が含まれています。粘性のある流体の中のばねの運動の場合、これに粘性抵抗力が加わり、
これは速度に比例する事が実験から分かっています。つまり、「１階微分」に比例する項が加わるという事です。
特性方程式が異なる２つ実数解を持つ場合は、粘性が結構強い場合になります。

■ 設定をして運動方程式を解く　■ どういう運動かを考察してみよう　

設定をして運動方程式を解く

まず、座標の設定としては、抵抗力のないばね運動の時と同じで、一次元の運動と考えてよいのです。ばねの平衡点を原点として、伸びる方向をプラス方向、縮む方向をマイナスとします。

次に、力を整理しましょう。ばねの力と、粘性抵抗力の２つがあります。粘性抵抗力は、運動を妨げる方向に働きますので、マイナス符号をつけるのです。（この抵抗力の符号の考え方は、空気抵抗力や摩擦力に対しても同じです。）

すると、運動方程式は次のようになります。 $$-kx-\rho \frac{dx(t)}{dt}=m\frac{d^2x(t)}{dt^2}$$ $$\Leftrightarrow \frac{d^2x(t)}{dt^2}+\frac{\rho}{m} \frac{dx(t)}{dt}+\frac{k}{m}x=0$$ $$\left(\Leftrightarrow \frac{d^2x(t)}{dt^2}+2\gamma \frac{dx(t)}{dt}+\omega^2x=0\hspace{10pt}\gamma=\frac{\rho}{2m},\omega^2=\frac{k}{m}\right)$$ 最後の形には別に変形しなくてもよいのですが、この形だと、解を出しやすいです。
いずれにしても、\(\frac{d^2}{dx^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0\) の形に確かになっています。

特性方程式が「異なる２つの実数解を持つ」という条件が満たされているとすると、上記の要領で解く事ができます。一応、特性方程式の解を出しておきましょう。（※２次方程式なので比較的容易に出せる事に注意してください。） $$特性方程式：X^2+2\gamma X+\omega^2X=0\Leftrightarrow (X+\gamma)^2-\gamma^2+\omega^2=0 $$ $$\Leftrightarrow (X+\gamma)^2=\gamma^2-\omega^2\Leftrightarrow X+\gamma=\pm \sqrt{\gamma^2-\omega^2}$$ $$\Leftrightarrow X=-\gamma \pm \sqrt{\gamma^2-\omega^2}$$ この２解（実数解という条件とします）を用いて、
微分方程式のほうの解は\(Ae^{(-\gamma +\sqrt{\gamma^2-\omega^2})t}+Be^{-\gamma -\sqrt{\gamma^2-\omega^2})t}\)
・・という事になります。

どういう運動かを考察してみよう

解が出ましたので「これで終わり」でもよいのですが、少し汚い形という事もあって、結局どういう運動になるのかが分かりにくいですね。そこで、もう少しだけ考察をしてみましょう。

特性方程式の２解の形をよく見ますと、 \(X=-\gamma \pm \sqrt{\gamma^2-\omega^2}\) は、これが実数解であるという前提で、
プラスマイナスのどちらの符号をとってもじつは「負の値」なのです。
平方根につくのがマイナス符号の場合は、最初の定数の取り方から X は必ず負の数ですし、
平方根につくのがプラス符号の場合でも \(\sqrt{\gamma^2-\omega^2}＜\gamma\) ですから、これは負の数になります。
(※分かりにくい場合、２乗してみてください。)

という事は、特性方程式の２解を、「正の定数」\(p,\hspace{5pt}q\hspace{5pt}を用いて X=-p,-q\)と書くと、 微分方程式のほうの解は、 $$x(t)=Ae^{-pt}+Be^{-qt}$$ となります。これだと多少見やすくて、p と q を正の数だとしましたから、これらにマイナスがついたものが指数に来ているという事は、時間に関して「単調減少」の関数であり、しかも変数の値が大きくなるとゼロに近づいていく事が分かります。 また、普通の指数関数ですので、三角関数と違って「振動」もしません。

この考察をまとめると、例えば次のような事が言えるのです。

特性方程式が２次方程式の場合、実数解を持つかは \(\sqrt{\gamma^2-\omega^2}\) の中身が正か負かで決まるわけですが、
\(\gamma =\frac{\rho}{2m}\) が粘性抵抗に由来する定数である事から、
粘性が強いほど特性方程式の解が実数解になりやすく、振動しない運動（過減衰）になりやすいという事です。
「では特性方程式が複素数解を持つ場合はどうなるのか？」と言いますと、結論は、
「振動しながら振幅が減衰し、時間が経つと原点（ばねの平衡点）に落ち着く」という運動になります。
ちなみに、特性方程式の解が重解の場合は、ぴったり合う事自体ほとんどないと考えられますが、減衰していく運動である事には変わりありません。

微積分学や物理の入門としては、まず「高校で教わった事を直接使える」ものについて、いくつか具体例を見ながら中に入っていけた事になります。同じように、まずは手持ちの知識を用いて入っていける部分から、少しずつ新規の知識も知っていくようにすると大学数学の内容に無理なく入っていけると思います。