円周率が極限値として存在する事は、同一円に対する内接正n角形と外接正n角形の周の長さのn→∞の時の極限値が存在する(両者は一致する)事によって証明します。
結論を言うと、証明の流れと発想自体は難しくないのですが、結構の計算などが一部結構面倒です。しかし省略せずに書いてるので適宜参照してください。
■ 証明のステップ
■ \(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) がともに存在する ■ \(\lim_{n_\to \infty}L_n=\lim_{n_\to \infty}R_n\) を示す
■ 3以上のどの自然数から始めても\(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) は同じ値に収束する
より初歩的な流れと考え方は「円周率はなぜ3.14なの?」に動画付きで書いています。

動画声優担当ステ♪様 http://sute.tabigeinin.com/
★この動画では円周率の値が3.14……である事のおおまかな流れを初歩的な部分から解説しています。
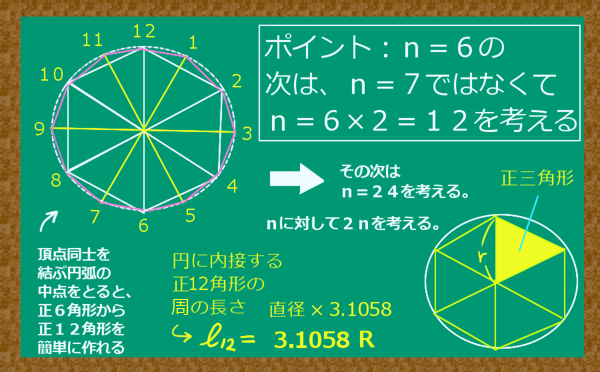
証明のステップ
これは少々手間がかかりますが、詳しく述べておきます。まず、次のように設定をします。
- 内接正n角形の周の長さ:\(L_n\)
- 外接正n角形の周の長さ:\(R_n\)
- 円の半径:1とする(一般のrでやっても同じ結果になります。)
$$L_nの2n等分: \frac{L_n}{2n}=a_n \hspace{15pt} R_nの2n等分: \frac{R_n}{2n}=A_n $$
そのうえで、次の手順により証明を行います。
- 任意の3以上の自然数に対して \(L_n<L_{2n}<R_{2n}<R_n\) を示す。
これは\(L_nとR_n\)が有界な単調数列である事、
つまり\(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) がともに存在する事を示す事になります。
式で示してもよいし、図形的にも示せます。 - \(\lim_{n_\to \infty}L_n=\lim_{n_\to \infty}R_n\) を示す。
これは、図形的考察から\(L_nとR_n\)に関する次の2公式(アルキメデスの公式とも)により示します。 $$R_{2n}=\large{\frac{2L_nR_n}{L_n+R_n}}$$ $$L_{2n}=\sqrt{L_nR_{2n}}$$ - 3以上のどの自然数から始めても\(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) は同じ値に収束する事を示す。
これは、n、2n、4n・・という形の数列であるために補足的に示すもので、通常のn=1,2,3,・・の形の数列であれば必要のない考察です。
図形的考察から、2以上の任意の自然数mに対して \(L_n<L_{mn}およびR_{mn}<R_n\) である事を示し、それにより証明します。
① \(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) がともに存在する
これは、次のステップで見るアルキメデスの公式を用いてもよいのですが、
図形的に三角不等式でも示せますから、まず図を見てみましょう。
上記でも触れましたようにnに対して2nを考える事で作図と計算が容易になります。
これに対して、nの次にn+1を考えると作図が非常に難しく、関係も複雑になってしまい非常に計算しにくくなってしまうのです。
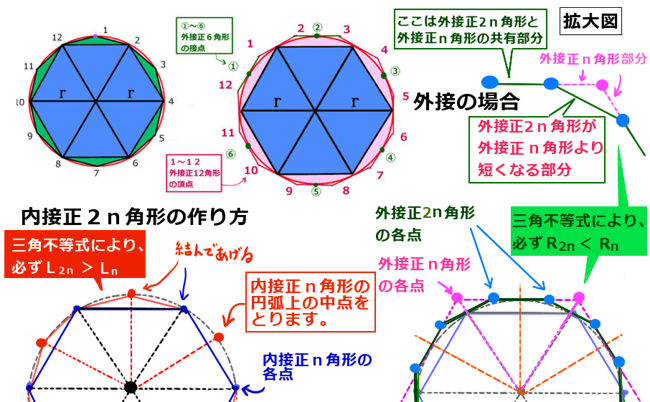
他方、外接のほうは、 正n角形と正2n角形とで 共有する点はありませんが部分的に共有する辺があります。
図を見ると(正6角形と正12角形の例ですが)、内接のほうは、正2n角形の2辺と正n角形の1辺からなる三角形に着目します。すると三角不等式によって\(L_n<L_{2n}\) が直ちに示されます。
外接のほうは、少し込み入るのですが、まず、図では次のように作図しています。
- 内接正n角形と内接正2n角形を、図の左側のように作図しておく
- 内接正n角形(正2n角形でもOK)の頂点での円の接線を引く。
- 接線同士をつなぎあわせてると、外接正n角形になる。
- 外接正n角形の各頂点から円の中心に向かって直線を引き、円との交点での接線を引く。
- 手順2と手順4で引いた接線を全て結び合わせると、 外接正2n角形になる。
この時、外接正n角形と外接正2n角形は共有する辺を持ちますが、共有しない部分もあります。その共有しない部分について三角不等式を適用すると、外接正2n角形の周の長さは、必ず外接正n角形の周の長さより小さい事になります。
よって、\(R_{2n}<R_n\) が示されます。
さらに、外接のほうの作図方法をよく見ると、内接正n角形の周の長さは外接正2n角形の周の長さよりも必ず短い事が分かります。(図形的に正確に言うと、相似な三角形の対応する辺同士になるので。)
よって、\(L_{n}<R_n\) です。
これは、任意の3以上の自然数で成立しますから、\(L_{2n}<R_{2n}\) でもあります。
すると、\(L_n<L_{2n}\) かつ \(L_{2n}<R_ {2n} \) より、\(L_n<L_{2n}<R_{2n}\) であり、
さらに \(R_{2n}<R_n\) でもあるのですから \(L_n<L_{2n}<R_{2n}<R_n\) が示されます。
よって、(解析学の基礎的な定理の証明は必要ですが、)次の事が示された事になります:
- \(L_n\) は 単調増加数列で上に有界であり\(\lim_{n_\to \infty}L_n\) は収束し、従って存在する。
- \(R_n\) は 単調減少数列で上に有界であり\(\lim_{n_\to \infty}R_n\) は収束し、従って存在する。
② \(\lim_{n_\to \infty}L_n=\lim_{n_\to \infty}R_n\) を示す。
さて、このようにして \(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) が収束する事が示されましたが、これだけだとじつは「同じ値に収束する」かは、分かりません。
別々の値に収束する可能性も否定できないのです。もしも、別々の値に収束するとすれば、一体どちらを正式な円周として採用すべきか、理論がぐちゃぐちゃになってしまいますね。
しかし実際は、両者は同じ値です。それを示します。
これを示すには、多少の手間はかかりますが \(L_nとR_n\)の関係を、図形的考察から強引に導出する方法が確実です。証明の中ではここが一番面倒くさいかもしれませんが、必要なのは平面幾何の基本知識だけです。
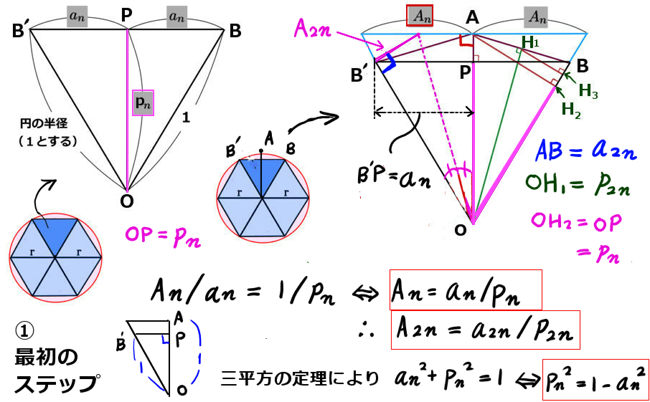
周の長さの2n等分\(\frac{L_n}{2n}=a_n と
\frac{R_n}{2n}=A_n\) は、ここで使います。
また、導出のポイントとして重要なのが、
「内接正n角形の隣り合う2点の中点と円の中心との距離」で、これを\(p_n\) とします。
図で言うと\(OP=p_n,\hspace{5pt}OH_1=p_{2n}\) です。
まず最初のステップとして、次の2式が得られます。三平方の定理から
- 内接正多角形で作られる三角形の相似から\(\frac{A_n}{a_n}=\frac{1}{p_n}\Leftrightarrow A_n=\frac{a_n}{p_n}\)
また、これにより(または同様の考察により) \(A_{2n}=\frac{a_{2n}}{p_{2n}}\) - 単純に三平方の定理により、\(a_n^2+p_n^2=1^2 \Leftrightarrow p_n^2=1-a_n^2\)
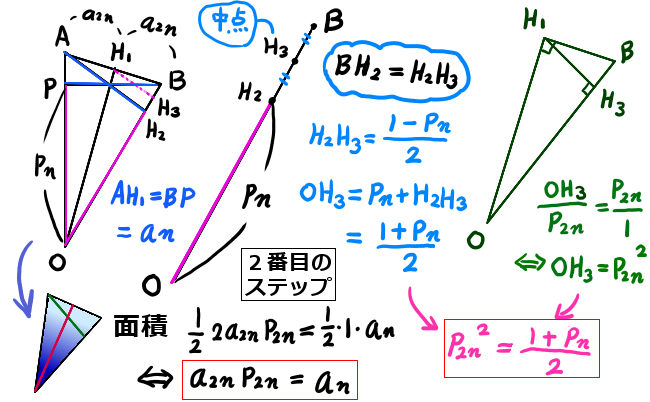
次のステップとして、図の三角形OABに着目した2式を得る事を考えます。片方は、同一面積を2つの辺と高さで表して得る式です。もう片方は、少々トリッキーですが図の\(OH_2\)の長さを2通りの方法で表す事によって得ます。
- 同一三角形の面積を2通りの方法で表す事により、\(a_{2n}p_{2n}=a_n\)
-
\(H_1 が AB の中点、H_3がBH_2 の中点\) である事により\(OH_3=p_n+\frac{1-p_n}{2}=\frac{1+p_n}{2}\)、
三角形の相似により \(OH_3=p_n^2\) となるので\(p_n^2=\frac{1+p_n}{2}\)\(\)
以上の式をまとめると、
- \(A_n=\frac{a_n}{p_n}\hspace{10pt}A_{2n}=\frac{a_{2n}}{p_{2n}}\hspace{10pt}p_n^2=1-a_n^2\)
- \(a_{2n}p_{2n}=a_n\hspace{10pt}p_n^2=\frac{1+p_n}{2}\)
これらを組み合わせると次の関係式が得られます。ちょっとだけ、計算の工夫は必要です。
$$A_{2n}=\frac{a_{2n}}{p_{2n}}=\frac{ a_{2n} p_{2n} }{ p_{2n} ^2}= =\frac{ 2a_{2n} p_{2n} }{ 1+p_{n} }=\frac{a_n}{ 1+p_{n} } = \frac{A_np_n}{ 1+p_{n} } =\frac{a_n}{A_n}\frac{A_n}{1+\frac{a_n}{A_n}}=\frac{a_nA_n}{a_n+A_n} $$
$$また、4a_{2n}^2=4\frac{a_n^2}{4p_{2n}^2}=\frac{2a_n^2}{1+p_n}=2a_n\frac{A_np_n}{1+p_n}=2a_nA_{2n} ∴ 2a_{2n}=\sqrt{2 a_nA_{2n} }$$
まとめると、次の2式になります。
$$ A_{2n}= \frac{a_nA_n}{a_n+A_n} \hspace{10pt} 2a_{2n}=\sqrt{2 a_nA_{2n} } $$
ここで、\(L_n=2na_n,R_n=2nA_n\) でしたから、整理すると次のように、目的の公式が得られます。
$$ L_{2n}= \frac{2L_nR_n}{L_n+R_n} \hspace{10pt} L_{2n}=\sqrt{ L_nR_{2n} } $$
これらのうちどちらを用いてもよいのですが、平方根のほうを使ってみましょう。
\(\lim_{n_\to \infty}L_n=\alpha,\hspace{5pt}\lim_{n_\to \infty}R_n=\beta\) とします。(収束する事は示しているので、このようにおいてよいわけです。)
$$すると、\alpha=\sqrt{\alpha \beta} ですから、\alpha^2= \alpha \beta \Leftrightarrow \alpha(\alpha – \beta)=0 $$
$$\alpha>0 ですから、\alpha=\beta ∴\lim_{n_\to \infty}L_n=\lim_{n_\to \infty}R_n$$
④ 3以上のどの自然数から始めても\(\lim_{n_\to \infty}L_nと\lim_{n_\to \infty}R_n\) は同じ値に収束する
さて、これでもう「証明終り。円周率は2つの数列の同じ極限値として確かに存在する」・・でも構わないのですが(一般にはそうしてます)、もう少し考察をしてみましょう。上記で示したのは、例えば正6角形から始めて、12,24,48,96・・とした場合に極限値が確かに存在し、正5角形から始めた場合は10,20,40,80,・・とした場合に、やはり確かに極限値が存在するという事です。
では、それらは確かに一致するでしょうか?
上記の証明ではnに対して2nを考えましたが、
じつはこれはnに対して3nでも4nを考えてもよいのです。
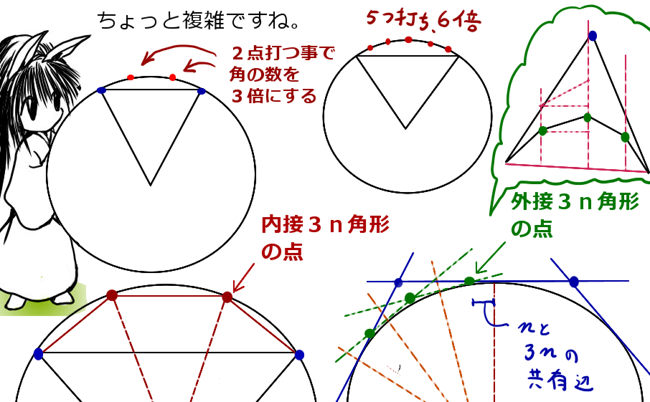
実際は任意の自然数mを使ってnに対する内接・外接正(mn)角形を用いる事で、上記同様の極限値の存在の証明ができます。(内接・外接ごとの極限値の存在まででじゅうぶんです。)
図形的に考えてみて、三角不等式の組み合わせか、適切に区切って傾きによる線分の長さを比較します。
それによって、\(L_n<L_{mn}<R_{mn}<R_n \) となる事が分かります。
つまり、上記では\(L_n<L_{2n}<R_{2n}<R_n \) を証明したわけですが、
同様に \(L_n<L_{3n}<R_{3n}<R_n \), \(L_n<L_{4n}<R_{4n}<R_n \),・・も成立するという事です。
さて、すると、例えば5と7で始めた場合で、5からの場合は7倍の角数、7の場合は5倍の角数を考えてみましょう。
それぞれ\(L_5,L_{35},L_{245},\cdots\) \(L_7,L_{35},L_{165},\cdots\) のような数列になります。
ここで、\(L_{35}\) から始めた場合も同様に収束するわけで、c に収束するとします。
ここで、\(\lim_{n\to \infty}L_{35n}=c\) とは、cを中心としたどんな小さい開区間にも、あるn以上の値の\(L_{35n}\) は全て含まれる事を意味します。【極限値は、解析学的にはそのように定義します。】
ここでそのようなあるn以上の、35 の倍数の中には、\(L_{5}やL_{7}\) から始まったものも含まれています。これらの数列が全て単調増加数列である事に注意すると、結局、そのあるn以上の値では、\(L_{5n},L_{7n},L_{35n}\) は全てcを中心とした同じ開区間内に含まれる事になります。これは、これらが同じ極限値 c を持つ事を意味します。
つまり、どんな(3以上の)自然数 n,m から始まろうとも、極限値は nm で始めた時と同じであるわけです。さらに別の自然数 N から始まるものを考えても nmN から始めた時と同じ値に収束するわけですから、結局どの番号から始めても、内接、外接の場合ともそれぞれ同じ値に収束する事を意味します。
また、同じ自然数から始まって倍にする数を変えたとしても、同じ考え方によって同じ値に収束する事になります。今、2倍にしていく場合は、内接と外接とで極限値が一致する事は証明済です。
これによって、内接正多角形と外接正多角形は n→∞ にした時に、確かに1つの極限値に収束すると言えます。これは、半径1の円に対して言えたわけですが、半径がrの場合は、三角形の相似により、周の長さはr倍になりますから極限値は半径が1の時の円周のr倍になります。
ですので、半径1の円の円周の長さを何かの定数の記号でおくのです。
結論を言うとこの定数を\(2\pi\) とおき、半径1つまり直径が2の円の円周の長さは\(2\pi\)であるとします。半径がrの場合は\(2\pi r\) となり、これは直径と円周率の積と言う事もできるわけです。
★ 3.14という値は?
上記の極限値としての円周率の存在証明では、円周率の値が具体的にいくらかという話が全く出てきていません。
しかし、このページの最初の概要で触れましたように、具体的な内接正n角形の周の長さについて、n=6の場合はぴったり「直径×3」、n=12の場合は「直径×約3.1058」となり、内接の場合はn=96(外接の場合はn=48)で3.14までの値は確定します。 【手計算でやる場合は、具体的な三角関数の値を半角の公式・マクローリン展開等で出すか表を見るなどして計算します。値が細かいので、結構面倒です。】
3.14以降の円周率の小数点の計算は、具体的に周の長さを計算する方法だとかなり大変なので、果てしなく小数点を出すような場合は何らかの「円周率を直接記述する公式」(基本的に無限級数)を用いて、しかもコンピューターに計算をやらせる事になります。
それらの「公式」は、円の面積を使う場合や、三角関数や逆三角関数(の微積分)をもとに作られている事が多いです。公式の種類によって、小数点計算が速い・遅いなどの特徴があります。マチン型の公式と呼ばれるものは計算が速く、逆にライプニッツ級数は収束が遅くて小数点計算には不向きです。
