無限級数とは？ | 理数系学習サイト　kori

このページでは無限級数について説明します。数学での無限の意味についても考えてみましょう。
【※あくまで数学での計算での扱いという意味で、哲学的意味などは別問題です。】

無限級数とは？その形と取り扱い方
無限は必ずしも抽象論ではない・・有限との裏返しの関係
無限級数の収束と発散

こちらは、このページで説明に用いているイラスト・漫画等のスライドです。

無限級数とは？その形と取り扱い方

数学で扱う無限とは「上限等の制限」を設けないという意味に近いです。物理では「十分大きい」等と言い換えられます。これが１つのポイントです。

「無限個の和」であっても、有限の範囲に「収束」すれば有限の数として扱える事が、数学でも物理でも１つの大きなポイントです。物理では、一度無限級数の形にしたうえで、計算結果に影響の少ない項を０とみなして少ない有限項の和に「近似」するという使い方も事も非常に重要です。

無限級数とは？無限個の項の和

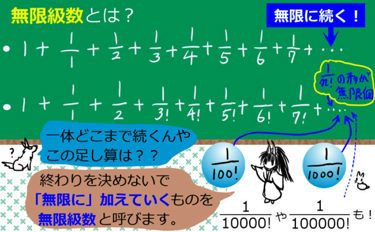
まずは、「無限級数」（infinite series）というものの「形」を、見てみましょう。
数学や物理で、こういうものがあったら、それを無限級数と呼ぶ、という事です。
無限級数の事を、単に「級数」と呼ぶ事もあります。その場合でも、「無限個の項の和」を表します。

「無限級数」(infinite series) の意味

無限級数とは、無限和とも言い、「無限個」の項の和で表される値、数列、関数などを指します。
項の数が、10個、100個、1000個、１億個、それ以上と、限りなく「無限に多くある」という事です。（※用語の使い方として、単に「級数」と言っても、それは無限級数を表します。）

$$例①（値・数列）：自然対数の底 e = 1+1+\frac{1}{2}+\frac{1}{3!}+\frac{1}{4!}+\frac{1}{5!}+\cdots$$ $$例②（値・数列）：調和級数 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots$$ $$例③（関数）：e^x のﾏｸﾛｰﾘﾝ展開\hspace{5pt} e^x= 1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots$$

これらの式の一番右にある「＋・・・」というのが、「無限級数」である事を表します。
また、あくまで表記の違いですが、和を表す「シグマ記号」$\Sigma$ と、「無限大」を表す$\infty$ を用いて、無限級数は次のようにも書かれます。 $$無限級数で表した\hspace{5pt}e\hspace{5pt}のシグマ記号での表記：\sum_{n=0}^{\infty}\frac{1}{n!}=e$$ $$全く同じものを、\lim_{n \to \infty}\sum_{j=0}^n\frac{1}{j!}=e\hspace{5pt}とも書きます。$$

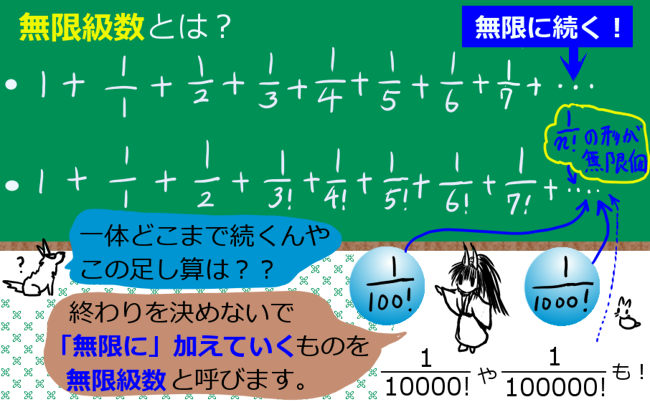
１＋２＋３＋４＋５＋６＋７＋・・・なども無限級数です。無限に加えていきます。項数が多くても（例えば１００万個）、有限の個数で止まるならそれはあくまで有限の和であり、数学では無限級数とは呼びません。（ただし、物理では。そのように「じゅうぶん大きい」数を「無限とみなす」事はよくあります。）びっくりマーク「！」は数学では「階乗」と言い、３！＝３×２、４！＝４×３×２、５！＝５×４×３×２、・・などを表します。
このページの後半でも触れますが、いわゆる無限小数も無限級数の仲間です。

このような無限項の和で表される形の数式があったら、それは無限級数である、という事です。
数列の形 $a_1+a_2+a_3+\cdots$ で書かれる事もあります。（シグマ記号を使えば $\sum_{n=1}^{\infty}a_n$）

和（つまり合計、足し算、加算）を表すシグマ記号で無限級数を表す場合は、「始まりの数」については、ｎ＝０からでもｎ＝１からでも、ｎ＝２からであっても、もっと大きいｎ＝１０００からであっても、終わりのほうが無限大であれば無限級数です。

！ちょっとだけ注意：点点点「・・・」の使い方

$1+\frac{1}{2}+\frac{1}{3}+\cdots$ や、$a_1+a_2+a_3+\cdots$ の「・・・」が、「無限」を表していると実質的に捉えてよいのですが、じつはこの「・・・」表記は、あくまで便宜的に使用しているようなところがあります。
「＋・・・」が、式の一番右に書かれていたら、それは「無限」を表すと思ってほぼ間違いないです。
他方で、この「・・・」という記号が、「『有限の項数』の和の間に書かれている」場合は、「有限項の和の『省略記号』」という意味になります。この点は、少し注意してください。
例えば次に記してあるのは、ある数列の「『n = 1000』までの和」です。この式でも「＋・・・＋」と書かれていますが、じつはこれは単に「1000 項も書くのが嫌なので」途中を「・・・」などと書いて省略しているだけなのです。従って、そのような場合は「無限個」を表しているのではなく、「有限個の項の表記上の省略」を表すという事になります。 $$S_{1000}=1+2+3+4+\cdots+999+1000\hspace{10pt}この場合の\cdotsは途中の有限個の和の「記載省略」の意味$$

では次に、そもそも「無限」というものを数学ではどのように考えるのか、どのように扱うかについて考えてみましょう。これは、何のために無限級数を考えるのかという、学ぶ目的とも大いに関係します。

無限は必ずしも抽象論ではなく、有限との裏返しの関係

「無限」を、数学では「どういう取り扱い」をするのかという事に絞ってシンプルに要点をつかみましょう。考え方自体は、非常にシンプルです。そのシンプルな考え方から始まって、いろいろな考察をする事により、様々な数学的事実や物理での使い道を探求する事が可能になります。

自然数と整数の場合の「無限」の扱い

どれだけ多くの項数があっても、「あるところで止まる」ならそれは「無限ではない」＝「有限である」という事です。数学的には、そこがポイントになります。

数学と言わず日常いつも使っている「数」には、上限を設けませんよね？
ポイントは、ものすごく大きい数・・例えば「１００億」などを考えても、それが「最大の数？」かというと、例えば「それよりも１だけ大きい数」などを、考えてもよいわけです。1000000000　に対して、 1000000000 + 1 = 1000000001 を考えてよいわけです。つまり、１，２，３・・と数える自然数は「無限に」大きくなります。

数学で言う「無限」とは一体何か？

無限大とは何かを数学的に説明すると、次のようになります。

「無限に大きい」とは：
どんな自然数（正の整数）Ｎを選んでも、「それよりも大きい別の数Ｍ」が必ず存在する
マイナス符号がついた負の数が無限大に「小さい」場合も考える事ができます。
どんな整数Ｎを選んでも、「それよりも小さい別の（負の）整数Ｍ」が必ず存在する

不等式で言いますと、自然数の場合、N₁ に対して N₁＜N₂ となる N₂ があって、
さらに N₂＜N₃ となる N₃ があって、・・・・と、続いて、
N₁＜N₂＜N₃＜N₃＜N₅＜N₆＜N₇＜・・・
非常に大きい自然数 10000000 を考えても、10000000 ＜ 10000001 という関係にある別の自然数 10000001 が、必ず存在する、という事です。

尚、あくまで文章表現の問題ですが、大学数学では、「どんな自然数Ｎを選んでも」という表現を、「任意の自然数Ｎに対して」と言う事が、よくあります。（このサイトでも使用します。）

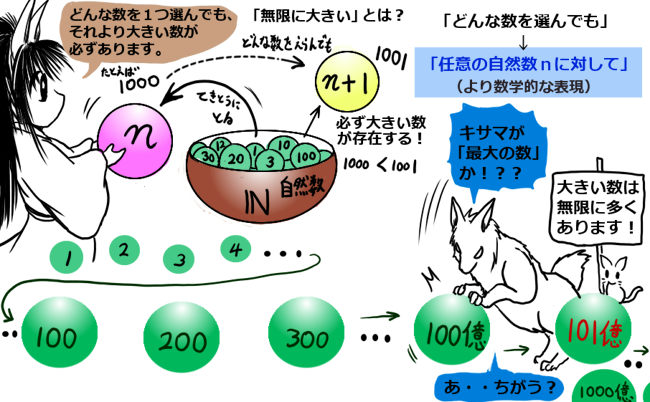
自然数や整数の全体には、「最大の数」や「最小の数」が存在しません。いくらでも大きい数、マイナス方向にいくらでも小さい数が存在する「無限集合」です。

自然数や整数の場合、大きさを増やしていくと、いくらでも大きくなる・・つまり「無限大」になるわけです。
ここで、条件として「自然数や整数の場合」と、限定している事には意味があります。じつは、有理数や実数と、少し話は変わるからです。

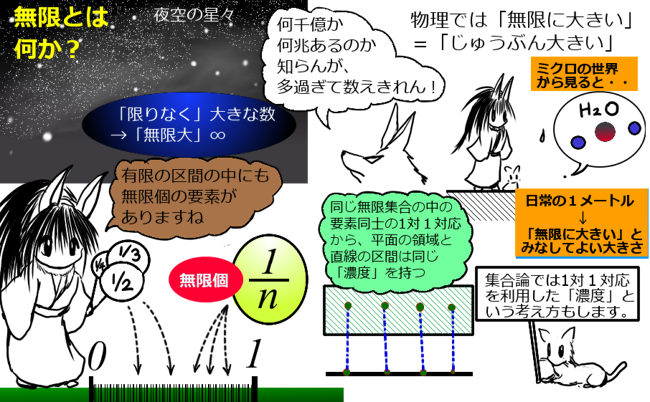
有理数や実数だと、有限の区間の中などにも、「無限個の数（要素）がある」という事も起こるのです。その事について、説明いたしましょう。理屈は、至って平易です。何も難しくはありません。

有理数と実数の場合の無限の扱い・・有限区間の中の無限個の要素

有理数や実数の「全体」で考えると、正の範囲では無限に大きくなるのは自然数や整数と同じです。
しかし、有理数や実数の場合、Q₁＜Q₂＜Q₃＜Q₄＜Q₅＜・・となって、尚かつ特定の数より必ず小さいという「集合」を、考える事ができるのです。

有理数とは、0.1, 0.2, 1/2, 1/3 などの、いわゆる「『整数の比による』分数で表せる数」です（自然数や整数を含めます）。
実数とは、有理数と $\sqrt{2},\pi, e$ などを含めたものです。
実数の「異なる２つの」要素には、必ず「大小関係」があります。どちらが大きい・小さいを必ず言えるという事です。
例えば、$-1 ＜ 0 ＜ 0.1 ＜\frac{1}{3}＜\frac{1}{2}＜1＜1.4＜\sqrt{2}＜2＜e＜3＜3.1＜\pi＜4＜・・・ $などの大小関係があります。

例えば、「0以上1以下」という、ごく限られた範囲の区間を、考えてみてください。この有限の区間の中にも、0.1, 0.2, 0.01, 0.001,・・等の、数えきれない、上限のない「無限個」の要素があるのです。
小数ではなくて分数で考えても同じ事で、1/2, 1/3 といった、「0より大きく1以下」の分数 $\frac{1}{n}$ は、無限個存在します。

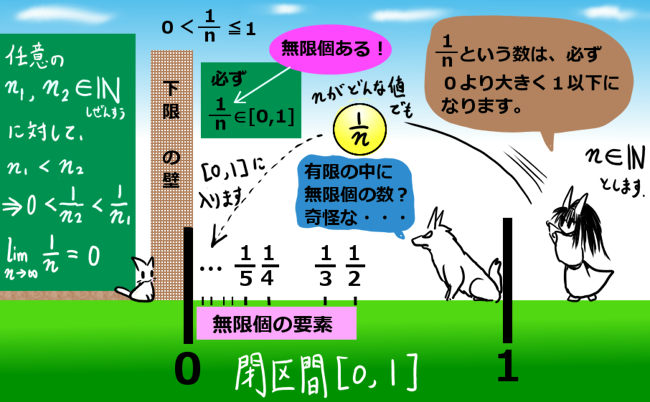
[0,1] という閉区間（０と１を含む、０以上１以下の区間）の中には、n を自然数として、1/nで表される有理数が無限に多く存在します。それらの個数は無限に多いけれども、0＜1/n≦1 という不等式を必ず満たします。大学数学の解析学では、このような時に数列 {1/n} は「有界」であると言います。

自然数が無限個あるので、自然数 n を用いた $\frac{1}{n}$ も、無限個あるのです。
（※整数の範囲だと、「0以上1以下」の区間に属する要素は「０と１」というただ２つの要素だけです。）

Point：有限の中にも「無限」は存在する！無限は必ずしも有限と根本的に違う世界にあるというわけではなく、むしろ隣り合わせにある事も多いのです。

１つの量や個数の「無限個」への分割
区間や領域の「無限個」の分割

後述しますように、区間や領域の無限個の分割は積分の考え方そのものですし、
幾何級数（等比級数）は、図形的に見ると有限の面積などを無限個に分割して加え合わせたものと見る事もできます。

このとき、$\frac{1}{n}$ という形に限定した有理数の集合の要素は、ｎを増やすごとに小さくなっていきます。
つまり、$\frac{1}{2}＞\frac{1}{3}＞\frac{1}{4}＞\frac{1}{5}＞\frac{1}{6}＞\frac{1}{7}＞\cdots$ という大小関係が、無限に続いていきます。しかし、これらは、どれほど小さくしても、「０よりは大きい」ですね。つまり、不等式で書くと次のようになります。 $$\frac{1}{2}＞\frac{1}{3}＞\frac{1}{4}＞\frac{1}{5}＞\frac{1}{6}＞\frac{1}{7}＞\cdots＞0$$ これは、
「２つの異なる要素同士の大小関係」については無限に小さくなっていくけれども、必ず０よりは大きい
という事です。

$$q_1＞q_2＞q_3＞q_4＞\cdots という条件も確かに満たしますが、$$ $$同時にq_1＞q_2＞q_3＞q_4＞\cdots ＞0 でもある；「任意の k に対して q_k > q_{k+1} かつ q_k＞0 」　$$

そして、このような事は、決して例外ではなく数多くあるという事が、１つの重要ポイントです。有限の実数の範囲の中に無限個の要素が存在するという事は、微積分の積分のほうの考え方に直結するものでもあります。

無限級数の収束と発散

さて、有理数や実数を考える場合、有限の区間の中にも無限個の数が含まれ得ると言う事を、お話しました。それと密接に関係する事として、無限個の項の和である無限級数も、有限の範囲におさまる場合があります。しかも、それは例外的にではなく、無限級数が有限の値になる事は多くあるのです。

無限級数が有限の値に確定する時、その無限級数は「収束」すると言います。
逆に、有限の値に確定しない場合を「発散」すると言います。特に、無限大の値になってしまう場合を「無限大に発散」すると言います。（有限の範囲内にはあるけれども極限値として一定の値に収束せず、「振動」する場合というのもあります。用語の使い方としては、「収束しない場合」の事を「発散」と呼びます。）

数学の理論においても、物理での応用でも、重要なのは「収束する」無限級数です。「発散」してしまうものは扱いにくいか、全く取り扱えないからです。

無限個加え合わせたら無限大？じつは必ずしもそうではなくて、無限大にはならず、有限の値に収束する場合もあるのです。基本的に、加え合わせる項の値がどんどん小さくなっていくものが該当します。大学数学の解析学では、どのような無限級数が「収束」し、そのような無限級数が「発散」するかの判定の理論が考察されます。

～有限の中の無限～　より身近で具体的な物で考えてみよう

１という有限の数・・現実的に言えば１ｋｇの物とか、１平方メートルの紙、１個の塊のケーキなど・・は、半分個に分割できます。$\frac{1}{2}$ という数を、考えているという事ですね。
同じように、３分割 $\frac{1}{3}$、４分割 $\frac{1}{4}$ を考える事も当然できるわけですが、
さらに大きい分割として「１万分の１」$\frac{1}{10000}$ なども考えられます。
（※ケーキを１万分割する事はまずないでしょうが、１立方メートル $\mathrm{m}^3$ などは１万分の１にすると１立法センチメートル$\mathrm{cm}^3$ ですので、対象によっては現実離れした考えというわけでもないのです。）
要するに、「〇〇分の１」$\frac{1}{n}$という数は、限りなく小さくする事ができるわけです。
このように、少なくとも数学的には「有限の中にも無限がある！」という事は、意外と「それほど不自然な発想ではない」と、言えるかと思います。

収束する無限級数の例

「収束する」タイプの無限級数の例を、いくつか挙げます。

収束する無限級数とは？意外と多くある！

$$自然対数の底 e = 1+1+\frac{1}{2}+\frac{1}{3!}+\frac{1}{4!}+\frac{1}{5!}+\cdots = 2.718・・・$$ $$円周率（ﾗｲﾌﾟﾆｯﾂ級数） \pi = 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots = 3.141592・・・$$ $$幾何級数（等比級数） 2 = 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\cdots$$ $$三角関数のﾏｸﾛｰﾘﾝ展開：任意の実数 x に対して \sin x = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$ $$そのほかの色々な無限級数の１例： 1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots$$

e = 2.718・・・は、無限小数なので小数点は無限に続きますが、値としては確かに有限の実数です。円周率を無限級数で表す公式もあり、しかも１つではなく、多くの種類があります。円周率の値は、もちろん3.14・・で、有限の値です。

このページでも後述しますが、幾何級数やテイラー展開、マクローリン展開なども、「収束」する無限級数の仲間です。（ただし、無制限に収束するわけではなく、収束する条件などがあります。大学数学での解析学の学習ポイントです。）

そのほかにも、$ 1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots$ や、$ 1+\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+\frac{1}{5^3}+\cdots$ なども、収束する無限級数です。このように、無限に加え合わせて「有限の値に収束する」ものは、決して例外的なものではなく、数学において意外と広く見られるものなのです。

無限大に発散する無限級数の例

他方で、無限個の項を加え合わせる事によって、普通に無限大に「発散」しまうものも、同じく多くあります。見た感じで明らかに発散するものと、判定が微妙なものがあります。

微妙な例としては「調和級数」と名のついた無限級数$ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$があります。
調和（harmonic）などと名前がついていますが、じつはこの無限級数は、無限大に発散します。相当項数を増やさないと大きな値にはならないのですが、じゅうぶん項数を増やすと、確かにいくらでも大きくなってしまい、収束しない事が証明されます。（証明自体はそんなに難しくありません。不等式を使った簡単な計算になります。）

無限大に発散する無限級数の例 $$調和級数：1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}++\frac{1}{5}\cdots$$ $$明らかに無限大になる例：1+2+3+4+5+6+7+\cdots$$ $$見ただけでは分からない微妙な例：\sum_{n=1}^{\infty}\frac{1}{\ln n}$$

無限級数の収束・発散について、特定のタイプのものについては解析学でのいくつかの判定法（ｺｰｼｰの判定法、ﾀﾞﾗﾝﾍﾞｰﾙの判定法）によって、公式のようなものを使って判定する事が可能です。
ただし、それで全ての無限級数の収束・発散を例外なく判定できるわけではありません。そこが、大学数学の解析学の面倒な部分でもあり、考察対象によっては「興味深い」部分でもあるのです。

無限級数には「収束」するものと、「発散」するものがある

項数が無限個ある和の形で表された値、数列、関数の事
無限級数は、値としては（関数などの場合は１つ１つの値について）次の２つの場合がある：
1. 有限の範囲に収まる（「収束する」）場合
2. 収束せず「発散する」場合
  特に無限大になる場合、マイナス無限大も含めて「無限大に発散する」と言う
→　どちらになるか、判定の方法が理論的にも応用的にも重要

参考：微分と積分も「無限」の数学・・物理でも無限級数を使う理由

微分係数は、関数を曲線と考えた時の「接線」ですが、非常に小さい区間の２点を結んだ傾きと考える事もできます。（その極限値が接線です。）
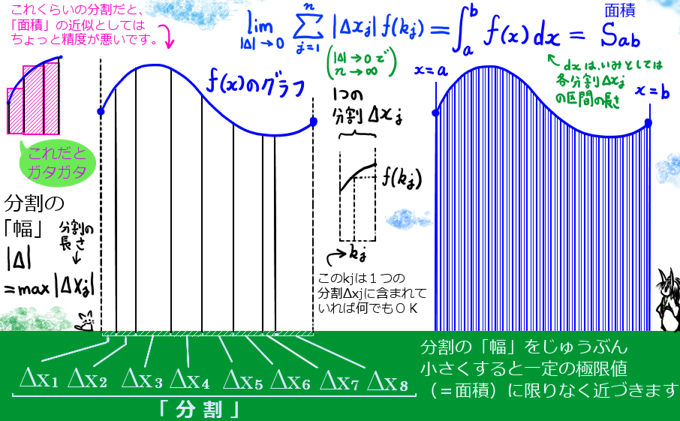
無限級数が関わるのは積分のほうがより明確で、積分とはそもそも無限個の長方形（ただし細長くて面積の小さい）の和でした。これは、無限級数であることに他なりません。

$$微分は「無限に小さい区間」の関数の変化率：\frac{df(x)}{dx}=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$ $$積分は「無限大に多く分割した」面積の和：\int_a^bf(x)dx=\lim_{|\Delta| \to 0}\sum_{j=1}^{\infty}|\Delta x_j| f(k_j)$$

また、微積分学の基本定理により、微分可能な関数は、「微分して得られた導関数」を積分したものと解釈する事もできます。その意味では、微分の積分＝無限級数として通常の関数を表現できる、とも言えるのです。
微分や積分は、物理に置いて非常に重要です。そして、微分や積分が無限級数に大きく関わるので、物理などへの応用にも無限級数は大いに関わるのです。
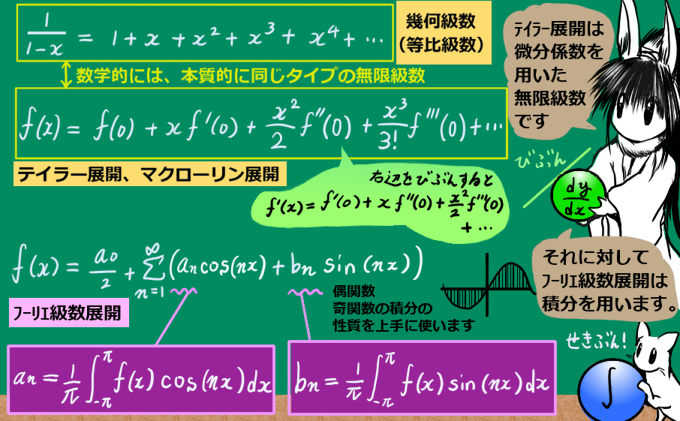
後述しますが、ﾏｸﾛｰﾘﾝ展開は微分を利用した無限級数であり、ﾌｰﾘｴ級数展開は、逆に積分を利用した無限級数展開です。
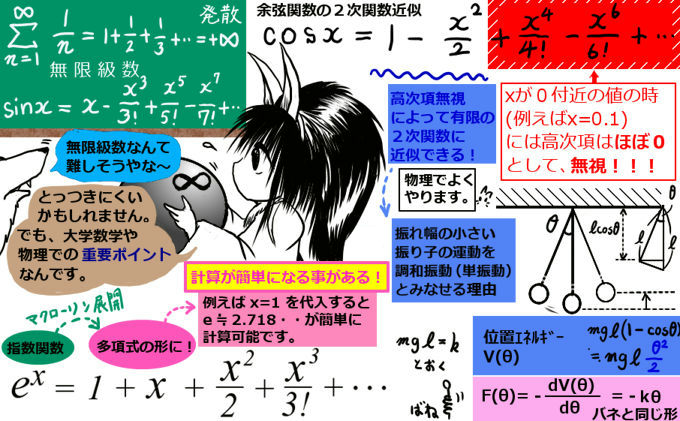
物理などでは、一度無限級数の形にしてから、高次の項をゼロに近似できるような範囲に絞って考え、実質的に有限の範囲で考えれるように工夫をする、という事もあります。これは、微分も積分も近似的には有限の範囲で数値計算的に扱う事が可能という事とも、大きく関わります。
そのような点にも注意してみてください。

積分も、意味としては無限級数のひとつです。

大学数学や物理を学んでいると、多分、唐突に「 f(x) を展開すると、・・」といった表現が使われるのを目にする事があると思います。これは、因数分解の逆の操作の「展開」の場合もありますが、割と多くの場合は「無限級数展開」を指しています。関数を「無限級数の形で表せますよ」という意味です。

具体的には、幾何級数（等比級数）展開、テイラー展開およびマクローリン展開、フーリエ級数展開などが無限級数展開の代表的なものです。

無限級数を扱う分野では微分を使って話を進める事も多いので分野としては微積分や解析学に含めて考える事が多いです。