カテゴリー: 証明と数学的論理

数学的帰納法（「すうがくてききのうほう」）は数学の命題や定理の証明を行う手段の１つで、整数や数列的な内容が含まれる命題や定理を証明する時に使える場合があります。

「帰納」とはどのような意味？

数学的「帰納」法と言いますが、
実は帰納という言葉自体は元々数学用語ではなくもっと一般的な語です。

「帰納」は「演繹（演繹）」と対になる語です。

• 帰納：個々の具体的事実から一般的・普遍的な法則や命題を導く事
• 演繹：一般的・普遍的な法則等から、より具体的な結論を導く事

ですので、例えばＡ_ｎ＝ｎ^２であるという事からＡ_１＝１，Ａ_２＝４，A_３＝９といった計算をする事は一般的に言うなら「演繹」に該当します。（ただし数学や理学系の学問ではその言葉は基本的に使用しません。）

では逆に、Ａ_１＝１，Ａ_２＝４，A_３＝９，A₄＝１６であれば「自然数ｎに対してＡ_ｎ＝ｎ^２」と言えるでしょうか？

数学ではそのように「予想」するところまではOKで、
「証明」として断定する事はNGになります。

１，４，９，１６という数が続いていたら「次は２５かな」という事は「予想」できるわけで、これは具体例からｎ^２という一般的な式を予想している事に他なりません。
実際、「ｎが自然数でｎ≦４の範囲」ではその予想は実際に正しいので「証明」にもなります。

しかし、ｎの範囲が１以上の全ての自然数であるなら、もしｎ＝１からｎ＝４まで「Ａ_ｎ＝ｎ^２」が正しくても、ｎ＝５以降においてはそれが正しい事は無条件には保証されないと数学では考えます。

例えば数学では極端な話「ｎ≦４の時はＡ_ｎ＝ｎ^２でｎ≧５の時はＡ_ｎ＝ｎ^３」などという数列を考えても構わないのです。つまり何の条件もなくて１，４，９，１６という数が続いているだけなら
「ｎ＝１からｎ＝４まではＡ_ｎ＝ｎ^２となり、ｎ≧５以降はそれが成立しない数列」は無限に多く考える事ができます。

そこで「数学的帰納法」ではそういった「予想」をもう少し発展させた考え方をして、命題について任意の自然数ｎに対して確かに成立する事を「証明」する方法と手順を明確にしています。

数学的帰納法による証明の手順

自然数を含む命題において、ｎ＝１，２，３・・・の全ての番号において命題が成立する事、つまり任意の自然数において命題が成立する事を数学的帰納法で証明する場合には次の事を行います。

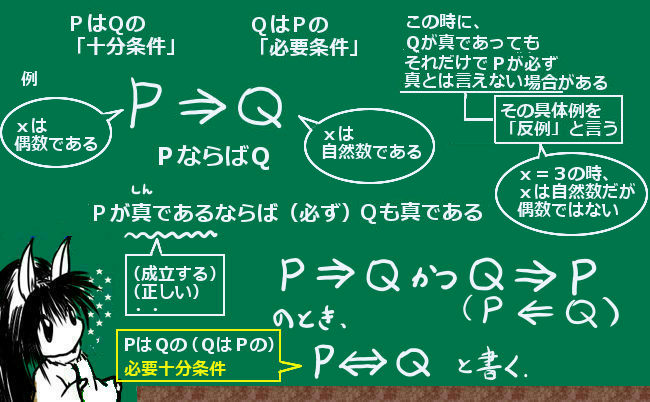
「ｎ＝ｋの時に命題が成立すると仮定してｎ＝ｋ＋１の時も成立する事を示す」というのは一体何をする作業なのかというと、「ｎ＝１の時に成立 ⇒ ｎ＝２の時も成立 ⇒ ｎ＝３の時も成立 ⇒ｎ＝４のときも・・・」という連鎖的な論理式をまとめて作る事に該当します。【⇒ は数学的な記号で「ならば」と読みます。参考：十分条件と必要条件】

文章表現としては「ｎ＝ｋの時に命題が正しいと仮定すると」「ｎ＝ｋの時に命題が真であると仮定すると」「ｎ＝ｋの時に・・である（命題の内容）と仮定すると」など、その一般的な番号で命題が正しい事を仮定するという意味が分かれば何でも構いません。

もう少し詳しく見ると任意の自然数ｋに対して「ｎ＝ｋで命題が成立する⇒ｎ＝ｋ＋１で命題が成立する」という「命題」を示して、もう１つ「ｎ＝１で命題が成立する」という事も示す事でｎ＝１で命題が成立する⇒ｎ＝２で命題が成立する⇒ｎ＝３で命題が成立する⇒・・・つまり「任意の自然数ｎにおいて命題が成立する」と言えて証明が完結する事になるわけです。

数学的帰納法を使ったほうがよい場合とは？

数学的帰納法は便利な証明方法ですが、数列的な式が含まれる命題なら何にでも使えばよいというわけではありません。例えば次の命題は数学的帰納法を使わずに直接証明をする事ができます。（これは自然対数の底 e の存在を証明する時に使う命題です。）

$$A_n=\left(1+\frac{1}{n}\right)^nとする時、任意の自然数nに対してA_n<3であり数列\{A_n\}は単調増加数列$$

この式の単調増加性を調べる時には数列の番号がｎ＋１の時の場合を考えますが、それは数学的帰納法における「ｎ＝ｋで正しいとしてｎ＝ｋ＋１でも正しい事を示す」事とは異なるのです。
この命題の単調増加性をもし数学的帰納法で証明するならA_２－A₁＞０を示してから
「Ａ_ｋ＋１－Ａ_ｋ＞０を仮定した時にＡ_ｋ＋２－Ａ_ｋ＋１＞０となる事を示す」というようになります。（それをしなくても実際はＡ_ｎ＋１－Ａ_ｎを直接計算すればＡ_ｎ＋１－Ａ_ｎ＞０を示せます。）

では、数学的帰納法を使用したほうが明らかによいと言える命題はどのようなタイプのものなのでしょうか。それは一概に方法論としては決められるものではないのですが、例えば次のような命題は数学的帰納法を使用したほうが良いと言えます。

$$f(x)=\mathrm{ln}xにおいて任意の自然数ｎに対して\frac{d^nf}{dx^n}=(-1)^{n-1}\frac{(n-1)!}{x^n}$$

つまり「ｎ階導関数」（微分をｎ回行った時の関数）が提示されている式である事を示すという命題です。ｌｎｘは自然対数関数であり、 log e x の事です。
また、式中の「！」記号は「階乗」の意味で、数を１ずつ減らして１になるまで掛け算し続ける操作を指します。例えば５！＝５×４×３×２×１＝１２０です。

このような命題の場合、具体的な微分を仮に頑張って数十回手計算で行ったとしても提示された式の形になると「予想」しかできません。考えている自然数ｎが微分という操作を行う「回数」であるために一般性を直接的に持たせにくいわけです。

そこで数学的帰納法を使うとこの手の命題は証明がしやすくなります。

まずｎ＝１の時はｄ／ｄｘ（ｌｎ）＝１／ｘであり、これ自体が自明な式ではなく証明が必要ですがそれはできているものとします。（微分の公式・対数関数の微分）

提示されている式に対してｎ＝１を代入してみて正しい事を確認します。

$$n=1の時、(-1)^{n-1}\frac{(n-1)!}{x^n}=\frac{1}{x}なので正しい。（0!=1という定義）$$

次に、ｎ＝ｋの時に正しいと仮定します。そのもとでｎ＝ｋ＋１の時にも正しい事をどのように言えばよいのでしょうか。ここでの場合はｎは微分を行う回数です。つまり、ｎ＝ｋの時の導関数を「もう１回微分」すればよいのです。

$$n=kの時命題が成立すると仮定すると\frac{d^kf}{dx^k}=(-1)^{k-1}\frac{(k-1)!}{x^k}$$

$$両辺をxで微分すると\frac{d}{dx}\left(\frac{d^kf}{dx^k}\right)=(-k)\cdot(-1)^{k-1}\frac{(k-1)!}{x^{k+1}}=(-1)^k\frac{k!}{x^{k+1}}$$

$$同時に\frac{d}{dx}\left(\frac{d^kf}{dx^k}\right)=\frac{d^{k+1}f}{dx^{k+1}}であるから、$$

$$\frac{d^{k+1}f}{dx^{k+1}}=(-1)^k\frac{k!}{x^{k+1}}=(-1)^{(k+1)-1}\frac{(k+1-1)!}{x^{k+1}}$$

よって、ｎ＝ｋ＋１の時も命題は成立しているので、任意の自然数ｎに対して命題は成立します。証明終わり、とするわけです。

本質的には前述のように「ｎ＝１の時に命題が成立」⇒「ｎ＝２の時に命題が成立」⇒「ｎ＝３の時に命題が成立」⇒・・という連鎖的な論理式が任意の自然数について成立する事が数学的に保証される事を証明したという事です。

必要条件、十分条件、必要十分条件の意味・覚え方・使い方などについて説明します。
必要条件と十分条件は対になっている考え方であり、ともに成立する場合には必要十分条件と言います。
（英：必要条件 necessary condition　十分条件 sufficient condition
　必要十分条件 necessary and sufficient condition）

ここでは高校数学で必要な知識を説明します。

★必要条件や十分条件そのものについて問う出題は高校数学特有のものですが、用語や考え方自体は大学数学でも使います。ただし、物理や工学などでは基本的には使用しません。

考え方と内容

「ＰならばＱ」という関係（「論理式」）が成立する時、ＰはＱの十分条件であると言います。
また、ＱはＰの必要条件であると言います。
記号では矢印記号「⇒」を使って「ならば」の部分を表し、 Ｐ ⇒ Ｑと書きます。

例えば「『ある実数が偶数である』ならば『その実数は自然数である』」といった感じです。
一般の定理などはそのような形をとっています。例えば三平方の定理は「『ある三角形が直角三角形である』ならば『斜辺と残り２辺の長さをそれぞれｃ、ａ、ｂとしてｃ^２＝ａ^２＋ｂ^２である』」という形です。
【※後述しますが三平方の定理に関してはこの逆も成立し、必要十分条件になります。】

この「ＰならばＱ」とは、「Ｐが成立するなら、必ずＱも成立している」という意味です。「必ず」というところがポイントで、例外は１つでもあってはいけないというのが数学での表現上のルールです。

「ＰならばＱ」Ｐ ⇒ Ｑ　と「ＱならばＰ」Ｑ ⇒ Ｐ　が両方とも成立する時、ＰはＱの必要十分条件であると言います。（この時、ＱのほうもＰの必要十分条件であると言います。）記号は、両方向に向いた矢印の「⇔」を使い、Ｐ ⇔ Ｑ と書きます。

Ｐ ⇒ Ｑ の関係が成立する時、「Ｑが成立するためには、Ｐが成立すれば十分である」といった表現をする事もあります。また、必要条件のほうに着目して「Ｐが成立するためには、Ｑが成立する事が必要である」と言う事もあります。

また文章の表現として、Ｐ ⇒ Ｑ の関係について「ＱはＰが成立するために『必要ではあるが十分ではない』」という表現がなされる場合もあります。これは、特に Ｑ ⇒ Ｐ は成立しない事が判明している場合に使われる事が多いです。（後にも触れますが、Ｐ ⇒ Ｑが判明しているけれどＱ ⇒ Ｐかどうかはまだ不明であるという場合もあり得ます。）

もう１つ例を挙げてみます。
Ｘが自然数の時、「Ｘが４の倍数である事」は「Ｘが偶数である事」の十分条件です。

これは、「Ｘが４の倍数」であれば必ず「Ｘは偶数」であるからです。
「Ｘが４の倍数である」 ⇒「Ｘは偶数である」　は、成立しています。

他方、Ｘが偶数であっても「必ず」４の倍数とは言えません。これは、例えば偶数であっても２や６といった数は４の倍数ではないからです。このように出てきてしまう「例外」の具体例の事を、数学の用語として反例と言います。

「Ｘが６の倍数である」事も「Ｘが偶数である」事の十分条件の１つです。
６の倍数６，１２，１８，２４、・・・は例外なく、必ず偶数であるからです。
つまり「Ｘが６の倍数である」 ⇒「Ｘは偶数である」　も成立しています。

このように、十分条件というものは複数あり得ます。

必要条件についても同様で、１つではなく複数あり得ます。
例えばここでの例で「Ｘが偶数である」を「Ｘが２以上の自然数である」といったものに変えても同様に
「Ｘが４の倍数の自然数である」 ⇒「Ｘは２以上の自然数である」　
は成立するので、Ｘが自然数の時に「Ｘが２以上の自然数である」事も「Ｘが４の倍数である」事の必要条件になります。

【図での覚え方】論理式と集合との関係

これら十分条件と必要条件の上手な捉え方として、ある変数が集合の元（要素）である事に関する論理式を考え、さらに図に描くという方法があります。この方法は、論理式の構造の理解のために大変便利です。

例えば「『ｘが集合Ｂに属する（Ｂの元である）』ならば『そのｘは集合Ａに属する』」という事が正しいとしましょう。この時、集合Ａと集合Ｂの包含関係は「ＡがＢを含む（Ａ⊃Ｂ）」という事になります。これは、この関係が成り立つという事は「ｘがＢに属するのであれば『必ず』そのｘはＡに属してもいる」という意味であるからです。

これらの集合が例えば平面上の領域（点の集まり）であれば、これは図形に描けます。絵としては、穴などがない領域Ａの中に完全に領域Ｂが含まれてしまっている場合です。この時に、領域Ａに完全に含まれてしまっている領域Ｂが、「十分条件」のイメージです。

逆に、相手方である領域Ｂを含んでいる大きなほうの領域Ａが、「必要条件」のイメージです。

領域ではなくて数直線上の区間で考えても同じで、
例えば実数ｘが閉区間 [０,１／２] に含まれるならば、ｘは閉区間 [－１,１]に含まれています。
記号で書くとｘ∊ [０,１／２] ⇒ ｘ∊ [－１,１] という事であり、
ｘ∊ [０,１／２] は ｘ∊ [－１,１] であるための「十分条件」であり、
ｘ∊ [－１,１]はｘ∊ [０,１／２]であるための「必要条件」です。
閉区間同士の包含関係については、[－１,１] が [０,１／２] を含んでおり [－１,１] ⊃ [０,１／２] です。

証明問題・計算での使い方

三平方の定理を証明する時は、まずは前提となる「直角三角形である」という条件が正しいとして、その時に必ず３辺の関係がｃ^２＝ａ^２＋ｂ^２となる事を示すわけです。

すると、その証明によって
『三角形が直角三角形である』⇒『斜辺と残り２辺の長さをｃ、ａ、ｂとしてｃ^２＝ａ^２＋ｂ^２である』
という論理式が真であるという事になるわけです。

しかし逆に、
『三角形の辺の関係式ｃ^２＝ａ^２＋ｂ^２が成立する』⇒『三角形が直角三角形である』
という事が正しいかはこの時点では分かりません。
この段階ではこの逆の形の論理式が「真か偽かも分からない」という事です。

従って、それが真か偽かもまた証明によって調べる必要があります。
今度は辺の長さの関係を前提として（正しいものとして）証明を行うわけです。

結論を言うと三平方の定理の「逆」である
『三角形の辺の関係式ｃ^２＝ａ^２＋ｂ^２が成立する』⇒『三角形が直角三角形である』
も、確かに成立します。証明できるという事です。
という事はＰ ⇒ Ｑ の形に対してＱ ⇒ Ｐの形も成立しているので、三平方の定理は「必要十分条件」である Ｐ ⇔ Ｑ の形となるわけです。

このように「必要十分条件である事を証明せよ」という問題の場合（入試問題以外でも）、
まず Ｐ ⇒ Ｑ を証明し、次に Ｑ ⇒ Ｐ も証明して Ｐ ⇔ Ｑ であると結論付けるのが一般的手法です。

通常の実数や文字式等の計算での式の変形も、じつは細かく言うと「必要十分条件」の関係です。

ｘ－ｙ＝０の時、ｘ＝ｙであるわけですが、
細かい事を言うとｘ－ｙ＝０⇒ｘ＝ｙかつｘ＝ｙ⇒ｘ－ｙ＝０であり、
ｘ－ｙ＝０⇔ｘ＝ｙというわけです。
そのため、式変形をする時に必要十分条件の記号⇔を使う事があります。

注意が必要な例として、平方根と２乗の関係があります。次の関係を見ましょう。ｘは実数とします。

$$x=\sqrt{2}\Rightarrow x^2=2$$

この論理式は成立します、しかし注意が必要なのは、この場合には「必要十分条件」で結ぶ事はできないという事です。それをやってしまうと、論理式は「偽」になってしまいます。理由は簡単で、２乗して２になる数（実数）は、\(\sqrt{2}\)は確かに当てはまるのですが、もう１つ負の数のほうの\(-\sqrt{2}\)があるためです。

$$特に条件が無い場合、x^2=2\Rightarrow x=\pm\sqrt{2}$$

この関係の逆は成立します。そのため、必要十分条件で結ぶのであれば次のようにする必要があります。

$$x^2=2\Leftrightarrow x=\pm\sqrt{2}$$

これを確実に見るには、ｘ^２＝２ ⇔ (ｘ＋\(\sqrt{2}\))(ｘ－\(\sqrt{2}\))＝０という因数分解された形にするとよいでしょう。【この「因数分解の形にする」という式変形は、必要十分条件で結ばれます。】

このように、一般の実数等での式変形であれば必ず必要十分条件になるわけではなく、時々片側にのみ
「ならば」記号の矢印⇒が成立する場合もあります。その点だけは少しだけ注意が必要になります。