必要条件、十分条件、必要十分条件の意味・覚え方・使い方などについて説明します。
必要条件と十分条件は対になっている考え方であり、ともに成立する場合には必要十分条件と言います。
(英:必要条件 necessary condition 十分条件 sufficient condition
必要十分条件 necessary and sufficient condition)
ここでは高校数学で必要な知識を説明します。
★必要条件や十分条件そのものについて問う出題は高校数学特有のものですが、用語や考え方自体は大学数学でも使います。ただし、物理や工学などでは基本的には使用しません。
考え方と内容
「PならばQ」という関係(「論理式」)が成立する時、PはQの十分条件であると言います。
また、QはPの必要条件であると言います。
記号では矢印記号「⇒」を使って「ならば」の部分を表し、 P ⇒ Qと書きます。
例えば「『ある実数が偶数である』ならば『その実数は自然数である』」といった感じです。
一般の定理などはそのような形をとっています。例えば三平方の定理は「『ある三角形が直角三角形である』ならば『斜辺と残り2辺の長さをそれぞれc、a、bとしてc2=a2+b2である』」という形です。
【※後述しますが三平方の定理に関してはこの逆も成立し、必要十分条件になります。】
この「PならばQ」とは、「Pが成立するなら、必ずQも成立している」という意味です。「必ず」というところがポイントで、例外は1つでもあってはいけないというのが数学での表現上のルールです。
「PならばQ」P ⇒ Q と「QならばP」Q ⇒ P が両方とも成立する時、PはQの必要十分条件であると言います。(この時、QのほうもPの必要十分条件であると言います。)記号は、両方向に向いた矢印の「⇔」を使い、P ⇔ Q と書きます。
数学において「PならばQ」 P⇒Q の関係が成立する時、次の呼び方をします。
- PはQの「十分条件」
- QはPの「必要条件」
- P ⇒ Q かつ Q ⇒ Pのとき、
PはQの「必要十分条件」(QはPの必要十分条件)
★「必要条件」のほうの名称の由来ですが、P ⇒ Q の関係が成立する時、「Qが偽であるならばPも偽である」という関係が成立するためと思われます。つまりPが真であるためには少なくともQは真でなければならず、Qが偽でPが真である場合はあり得ないという事です。(他方P ⇒ Q の時に、Qが真でもPが真である事は確定しません。Qが真でPが偽の場合はあるのです。そこが十分条件と異なります。)
この関係は、後述する図によるイメージで理解が進むかと思います。
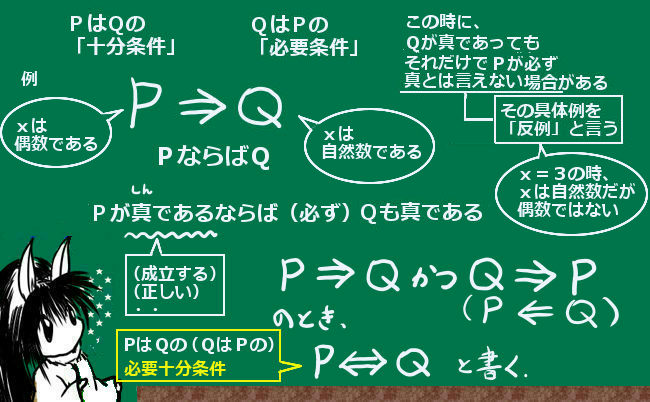
P ⇒ Q の関係が成立する時、「Qが成立するためには、Pが成立すれば十分である」といった表現をする事もあります。また、必要条件のほうに着目して「Pが成立するためには、Qが成立する事が必要である」と言う事もあります。
また文章の表現として、P ⇒ Q の関係について「QはPが成立するために『必要ではあるが十分ではない』」という表現がなされる場合もあります。これは、特に Q ⇒ P は成立しない事が判明している場合に使われる事が多いです。(後にも触れますが、P ⇒ Qが判明しているけれどQ ⇒ Pかどうかはまだ不明であるという場合もあり得ます。)
★このときのPやQは数学的に意味のあるものを考えます。
「今朝は晴れだった」とか「この理論は美しい」とかそういう文章の類は入れないわけです。
もう1つ例を挙げてみます。
Xが自然数の時、「Xが4の倍数である事」は「Xが偶数である事」の十分条件です。
これは、「Xが4の倍数」であれば必ず「Xは偶数」であるからです。
「Xが4の倍数である」
⇒「Xは偶数である」 は、成立しています。
他方、Xが偶数であっても「必ず」4の倍数とは言えません。これは、例えば偶数であっても2や6といった数は4の倍数ではないからです。このように出てきてしまう「例外」の具体例の事を、数学の用語として反例と言います。
「Xが6の倍数である」事も「Xが偶数である」事の十分条件の1つです。
6の倍数6,12,18,24、・・・は例外なく、必ず偶数であるからです。
つまり「Xが6の倍数である」
⇒「Xは偶数である」 も成立しています。
このように、十分条件というものは複数あり得ます。
必要条件についても同様で、1つではなく複数あり得ます。
例えばここでの例で「Xが偶数である」を「Xが2以上の自然数である」といったものに変えても同様に
「Xが4の倍数の自然数である」
⇒「Xは2以上の自然数である」
は成立するので、Xが自然数の時に「Xが2以上の自然数である」事も「Xが4の倍数である」事の必要条件になります。
【図での覚え方】論理式と集合との関係
これら十分条件と必要条件の上手な捉え方として、ある変数が集合の元(要素)である事に関する論理式を考え、さらに図に描くという方法があります。この方法は、論理式の構造の理解のために大変便利です。
例えば「『xが集合Bに属する(Bの元である)』ならば『そのxは集合Aに属する』」という事が正しいとしましょう。この時、集合Aと集合Bの包含関係は「AがBを含む(A⊃B)」という事になります。これは、この関係が成り立つという事は「xがBに属するのであれば『必ず』そのxはAに属してもいる」という意味であるからです。
これらの集合が例えば平面上の領域(点の集まり)であれば、これは図形に描けます。絵としては、穴などがない領域Aの中に完全に領域Bが含まれてしまっている場合です。この時に、領域Aに完全に含まれてしまっている領域Bが、「十分条件」のイメージです。
逆に、相手方である領域Bを含んでいる大きなほうの領域Aが、「必要条件」のイメージです。
★ここで、もしもx∊B ⇒ x∊A という情報だけがあって領域AとBの実際の様子は分からない場合には、論理式の逆の「x∊A⇒x∊B」が成立するかはその段階では「不明」という事になります。
ただし、その場合でも領域Aが領域Bを含んでいる事は確定しています。しかし、A⊃Bであると同時にB⊃Aでもある可能性、つまり領域AとBが完全に一致している場合も考えられるわけです。

領域ではなくて数直線上の区間で考えても同じで、
例えば実数xが閉区間 [0,1/2] に含まれるならば、xは閉区間 [-1,1]に含まれています。
記号で書くとx∊ [0,1/2] ⇒ x∊ [-1,1] という事であり、
x∊ [0,1/2] は x∊ [-1,1] であるための「十分条件」であり、
x∊ [-1,1]はx∊ [0,1/2]であるための「必要条件」です。
閉区間同士の包含関係については、[-1,1] が [0,1/2] を含んでおり [-1,1] ⊃ [0,1/2] です。
証明問題・計算での使い方
三平方の定理を証明する時は、まずは前提となる「直角三角形である」という条件が正しいとして、その時に必ず3辺の関係がc2=a2+b2となる事を示すわけです。
すると、その証明によって
『三角形が直角三角形である』⇒『斜辺と残り2辺の長さをc、a、bとしてc2=a2+b2である』
という論理式が真であるという事になるわけです。
しかし逆に、
『三角形の辺の関係式c2=a2+b2が成立する』⇒『三角形が直角三角形である』
という事が正しいかはこの時点では分かりません。
この段階ではこの逆の形の論理式が「真か偽かも分からない」という事です。
★P ⇒ Q が成立している時に矢印の先のほうのQを必要条件と呼ぶわけですが、この時に Q ⇒ P が成立するかどうかが判明しているとは限りません。
一般には特別な条件が明示されていない限りは、P ⇒ Qの成立からQ ⇒ Pの真偽を直ちに判定する事はできないので、その真偽を明確にするために「証明」という作業を行います。
従って、それが真か偽かもまた証明によって調べる必要があります。
今度は辺の長さの関係を前提として(正しいものとして)証明を行うわけです。
結論を言うと三平方の定理の「逆」である
『三角形の辺の関係式c2=a2+b2が成立する』⇒『三角形が直角三角形である』
も、確かに成立します。証明できるという事です。
という事はP ⇒ Q の形に対してQ ⇒ Pの形も成立しているので、三平方の定理は「必要十分条件」である P ⇔ Q の形となるわけです。
このように「必要十分条件である事を証明せよ」という問題の場合(入試問題以外でも)、
まず P ⇒ Q を証明し、次に Q ⇒ P も証明して P ⇔ Q であると結論付けるのが一般的手法です。

通常の実数や文字式等の計算での式の変形も、じつは細かく言うと「必要十分条件」の関係です。
x-y=0の時、x=yであるわけですが、
細かい事を言うとx-y=0⇒x=yかつx=y⇒x-y=0であり、
x-y=0⇔x=yというわけです。
そのため、式変形をする時に必要十分条件の記号⇔を使う事があります。
注意が必要な例として、平方根と2乗の関係があります。次の関係を見ましょう。xは実数とします。
$$x=\sqrt{2}\Rightarrow x^2=2$$
この論理式は成立します、しかし注意が必要なのは、この場合には「必要十分条件」で結ぶ事はできないという事です。それをやってしまうと、論理式は「偽」になってしまいます。理由は簡単で、2乗して2になる数(実数)は、\(\sqrt{2}\)は確かに当てはまるのですが、もう1つ負の数のほうの\(-\sqrt{2}\)があるためです。
$$特に条件が無い場合、x^2=2\Rightarrow x=\pm\sqrt{2}$$
この関係の逆は成立します。そのため、必要十分条件で結ぶのであれば次のようにする必要があります。
$$x^2=2\Leftrightarrow x=\pm\sqrt{2}$$
これを確実に見るには、x2=2 ⇔ (x+\(\sqrt{2}\))(x-\(\sqrt{2}\))=0という因数分解された形にするとよいでしょう。【この「因数分解の形にする」という式変形は、必要十分条件で結ばれます。】
少し話が込み入りますが、もしも「xは正の数」という条件があるのであれば、上記の右方向だけの \(x=\sqrt{2}\Rightarrow x^2=2\) は必要十分条件で結んでも間違いではありません。これは「x>0かつ\(x^2=2\)」という具合に、条件自体が変わるためです。
このように、一般の実数等での式変形であれば必ず必要十分条件になるわけではなく、時々片側にのみ
「ならば」記号の矢印⇒が成立する場合もあります。その点だけは少しだけ注意が必要になります。
