因数分解と言えば中学数学で悪名高いものの1つかと思います。
これをめぐる話は色々あるのですが、まず数学の教員すらもよく言ってしまう「まとめる」という言葉で因数分解を表現する事に、じつはひとつの問題があります。その事についても見ていきましょう。
因数分解は積の形に「分解」する事
日常で使う因数分解
因数分解は、「分解」です。
1つの数を、2つ以上の「積」の形に分解する事を言います。
その意味で、50=10×5のような形で表す事はやっている事としては因数分解です。
合計50円の物を買うために10円玉を5枚取り出すという時には、
じつは因数分解の思考をしているのです。
50=5×5×2と表せるように、A=B×C×Dのような3つ以上の積で表す事も指します。
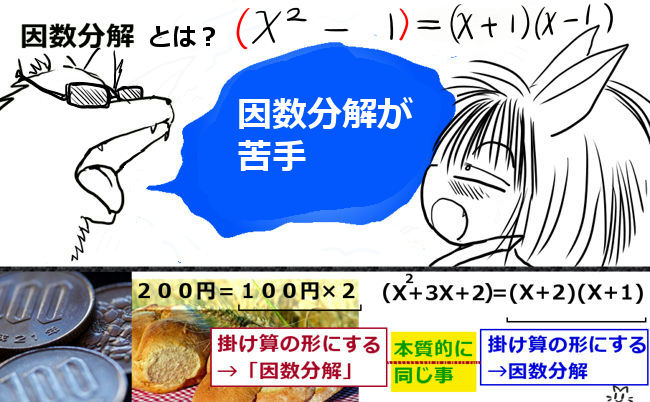
因数分解を「何に使うのか」という事は頻繁に言われる事ですが、じつのところ日常の生活でも使われる、数に関する操作と思考の1つが因数分解なのです。
掛け算は普段から使う計算だと思いますが、2×3=6に対して、これを逆に見て6=2×3という見方をする事が因数分解の考え方と言ってもよいかと思います。
中学校等での式の因数分解
さてしかし、そうは言っても、多くの人が問題としているのは次のような「式の」因数分解の事でしょう。
$$x^2+2xy+y^2=(x+y)^2,\hspace{10pt}x^2+3x+2=(x+1)(x+2)\hspace{10pt}等$$
で、こういう問が出題される時に、教員もよく言ってしまうのが、「まとめる」という表現です。そう言いたくなる気持ちは分かりますし、実際上、便利な表現だとも思います。
しかし、このように式に関する因数分解も、操作としてはまとめているのではなく「分解」しているのです。上記の因数分解を、もう1度書いてみましょう:
$$(x^2+2xy+y^2)=(x+y)^2=(x+y)(x+y),\hspace{10pt}(x^2+3x+2)=(x+1)(x+2)\hspace{10pt}等$$
どうでしょうか?
これだと、1つの数を2つ以上の数の積に「分解」している事が分かりやすいのではないでしょうか。50=10×5として表すのと全く同じなのです。
通常は、左辺のかっこはなくても同じ意味になるので省略してしまいますが、式の場合であっても複数の積の形に「分解」して表す事も可能であるというのが中学や高校で教わる因数分解の意味なのです。
因数分解を行う事が有用であるのは、何と言っても方程式の解が得られる事にあります。これは、実数や複素数についての 「A×B=0 ⇔ A=0またはB=0」 という性質を利用しているのです。(※高校以上で学ぶ「行列」などについてはこの関係式が成立しないので注意。)
$$(x+1)(x+2)=0\Leftrightarrow x=-1\hspace{5pt}または\hspace{5pt}x=-2$$
$$したがって、x^2+3x+2=0の\hspace{5pt}解は、x=-1\hspace{5pt}または\hspace{5pt}x=-2$$
こういった具合に計算ができるので、数学、自然科学、工学の理論で使われるというわけです。
因数分解のコツ
学ぶ「意味」は分かったとしても、それでも計算問題として苦手であるという人もいるかと思います。
ではうまく計算して得意になるコツはあるのかというと、人によってやり方は多少違うので一概には言えませんが、その1つをここで挙げてみたいと思います。
$$■問い:x^2+15x+56\hspace{5pt}の因数分解はどのようになりますか。$$
こういった問題があった時には「定数項」に着目するとよい場合が多いです。
すなわち、上式では56の部分です。
因数分解とは逆に式を展開する時の事を考えると分かりやすいのですが、
$$(x+a)(x+b)=x^2+(a+b)x+ab$$
ですから、上記のような2次式の因数分解を考える場合、定数項を何らかの「2つの数の掛け算」として表す事がヒントになります。この2つの数とは任意の実数であったり複素数でもいいわけですが、中学校で問われる問題の場合、大抵は整数だと思います。
56の場合、1×56、2×28、4×14、8×7などの表現方法があります。(できれば頭の中で思い浮かべられると、試験の時は楽です。)
次に1次の項\(15x\)に着目し、1×56、2×28、4×14、8×7の数の組み合わせのうち、加えたら15になる数はあるかというと、8と7の組み合わせが該当しますね。従って、因数分解は次のようになるのです:
$$x^2+15x+56=(x+8)(x+7)【解答】$$

このように「綺麗な形ですんなりと」因数分解を見つけられないケースも当然ありますが、学校で出題される問題は解けるように作ってあるので、大抵は綺麗な数の組み合わせである事が多いと思います。
式にマイナスが入っている場合の考え方も同じで、
$$x^2-7x-18$$
の因数分解は、掛けて -18になって、今度は(マイナスも含めて)加えると -7 になる組み合わせを考えます。この場合は、-9 と 2 が該当しますので、次のように因数分解できます。
$$x^2-7x-18=(x-9)(x+2)$$
因数分解に関する応用問題
中学~高校の問題
さて、学校で出題される問いは上記のようにある程度分かりやすいものである事が普通ですが、次のような「汚い式」の因数分解はどうすればよいでしょう。
$$■問い:x^2+\sqrt{2}x-6\hspace{5pt}の因数分解はどのようになりますか。$$
これを見て、因数分解は「できない」のではないか?と思う人もいるかもしれませんが、因数分解はできます。綺麗な形には到底ならないという前提付きですが・・。
こういった問題は普通はあまり出ないとは思いますが、高校入試や、考え方自体は大学入試のセンター試験程度では出題される可能性はあるかもしれません。

理屈としては、二次方程式は異なる2つの解か、重解1つを必ず持ちます。しかも、これは手計算で解を出す事ができます。
$$x^2+\sqrt{2}x-6=0を満たす\hspace{5pt}x=\alpha\hspace{5pt}または\hspace{5pt}\beta\hspace{5pt}は存在し、(x-\alpha)(x-\beta)=0となる$$
という事を利用して「因数分解」が可能であるという事です。ですから、因数分解しなさいと言ってますが、実質的には2次方程式を解くという問題なのです。
$$\left(x+\frac{\sqrt{2}}{2}\right)^2-\frac{1}{2}-6=0$$
$$\Leftrightarrow \left(x+\frac{\sqrt{2}}{2}\right)^2=\frac{13}{2}$$
$$\Leftrightarrow x+\frac{\sqrt{2}}{2}=\pm\frac{\sqrt{26}}{2}$$
$$\Leftrightarrow x=\frac{-\sqrt{2}\pm\sqrt{26}}{2}$$
方程式にした場合の2つの解が分かりましたので、これで「因数分解」できます。
$$x^2+\sqrt{2}x-6=\left(x-\frac{-\sqrt{2}+\sqrt{26}}{2}\right)\left(x-\frac{-\sqrt{2}-\sqrt{26}}{2}\right)$$
$$=\left(x+\frac{\sqrt{2}-\sqrt{26}}{2}\right)\left(x+\frac{\sqrt{2}+\sqrt{26}}{2}\right)【解答】$$
尚、仮にこういう問いが出題されて答えの形が汚くて合ってるかどうか不安になる時はチェックをするとよいでしょう。因数分解したものを、逆に展開してみてもとの式に一致するかを見ればよいのです。
二次方程式の「解と係数の関係」として考えても同じです。
$$(x – \alpha)(x – \beta)=x^2-(\alpha+\beta)x+\alpha\beta$$
解と係数の関係を使う場合、プラスマイナスの符号に多少の注意が必要です。
ここでは、因数分解された最後の結果を展開する事でチェックしてみましょう。
$$\left(x+\frac{\sqrt{2}-\sqrt{26}}{2}\right)\left(x+\frac{\sqrt{2}+\sqrt{26}}{2}\right)\hspace{5pt}を展開計算します。$$
$$\frac{\sqrt{2}-\sqrt{26}}{2}+\frac{\sqrt{2}+\sqrt{26}}{2}=\sqrt{2},\hspace{10pt}\frac{\sqrt{2}-\sqrt{26}}{2}×\frac{\sqrt{2}+\sqrt{26}}{2}=\frac{2-26}{4}=\frac{-24}{4}=-6$$
このようになるので、正しく因数分解できている事を確認できます。
■参考:3次式の因数分解
一般の3次式を因数分解する方法も基本は2次式と同じですが、一般の3次方程式の解を手計算だけで出すのは結構面倒なので、てきとうな「簡単な1つの解」を見つけさせて、「1次式と2次式の積」の形の因数分解をさせる問いのほうが、出題されるとすれば多いのではないかと思います。
例えば、
$$x^3-x^2-x-2$$
という3次式の因数分解では、じつはこの式に \(x=2\) を代入すると 0 になるので、
まず \((x-2)\) が1つの因数(掛け算を構成する項の1つ)であると分かるのです。
つまり、もとの3次式の因数分解は $$x^3-x^2-x-2=(x-2)(x^2+Ax+B)$$ の形になります。ここで、定数項に着目すれば $$-2=-2B\Leftrightarrow B=1$$ であり、1次の項は $$-1=B-2A=1-2A\Leftrightarrow -2=-2A\Leftrightarrow A=1$$ という事になりますから、これで解答を出せるわけで $$x^3-x^2-x-2=(x-2)(x^2+x+1)$$ と、因数分解できます。2次式の部分をさらに因数分解する事も可能です。
大学数学での問題
大学数学の範囲だと、全体の中の位置付けとしてはそれほど重要ではないのですが、一応存在するテーマとして「無限級数の因数分解」というものがあります。例えば次のようなものです:
$$1-\frac{x^2}{6}+\frac{x^4}{120}-\frac{x^6}{5040}+\cdots=\left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)\cdots$$
左辺は和が無限に続く「無限級数」で、右辺はそれが因数分解され無限個の積の形になった「無限積」です。
\(\pi\) は円周率で 3.14・・を表します。
もちろん、魔法のように唐突にこの関係式が得られるのではなく、1つ1つの数学的事実を組み合わせると、結果としてはこのような関係式も成立する事が分かる、というものです。
この関係式を得るには少々面倒な手続きがあって、まず左辺の無限級数は、じつは微積分の知識を使って出てくるものなのです。【正弦関数のマクローリン展開を x で割ったものです。】
そして、それを「因数分解」する時に、そもそも無限級数を無限積の形に「因数分解してよいのか?」という問題もじつはあります。これについても、極限や微積分に関する分野での考察が必要になります。これは、厳密に考えると結構面倒です。
いずれにしても中学でも高校でも大学でも、因数分解において重要な考え方は「積の形にする」という事なのです。