積の微分公式と、それの変形版である商の微分公式の内容、具体例、証明について述べます。
(英:product rule, quotient rule)
これは関数同士の「掛け算」「割り算」の形になっている関数を微分する時に成立する公式です。
積と商の形の関数は統一的に捉える事ができるので同時に記します。
詳しくは後述していますが、商の場合にはf(x)と1/g(x)の「積」と捉えればよいので基本的には同じ形の公式なのです。
公式の内容
y=xex といった関数同士の「積」の形になったものを微分する時には積の微分公式が使えます。
また、正弦関数を「x で割った」(sin x)/x などには商の微分公式が使えます。
関数f(x)とg(x)の積f(x)g(x)、商f(x)/g(x) を微分した時には次の公式が成立します。
ここで、f(x)とg(x)をf、gと記しています。
$$積の微分公式:(fg)^{\prime}=f^{\prime}g+fg^{\prime} \hspace{20pt}商の積分公式\left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime}g-fg^{\prime}}{g^2}$$ これらは本質的には全く異なる公式ではなく、同種類のものであると捉えたほうがよいでしょう。
商の微分については、分母にあるのは「『微分してない g(x)』の2乗」です。
積の微分公式については、2つの項は足し算なので順番はどっちでもよいのですが、
「f’g +fg’」の順番にしたほうが、商の微分公式との関係で「覚えやすい」かとは思います。

計算の具体例
公式を使って計算する手順としては、f(x) と g(x) のそれぞれについて「x で微分した関数」と、「微分してない(もともとの)関数」をパーツとして用意し、公式に当てはめて丁寧に計算するというものになります。
まず、積の微分公式の具体的な計算の例をいくつか見てみます。
- y=sinx cosx 【2つの三角関数の積】の微分は次のようになります。$$\frac{d}{dx}\{(\sin x)(\cos x)\}
=(\sin x)^{\prime}(\cos x)+(\sin x)(\cos x)^{\prime}
=\cos^2x-\sin^2x$$
加法定理を考えると、この結果はcos 2x に等しくなります。sin x cos x=(sin 2x)/2 として、xで微分した時の結果と一致します。(この時、合成関数の微分公式を使用しているので注意。) - y=sin2x の微分を考えます。
これに積の微分公式を適用する場合にはy=(sin x)・(sin x)と考えるわけです。$$\frac{d}{dx}\{(\sin x)(\sin x)\} =(\sin x)^{\prime}(\sin x)+(\sin x)(\sin x)^{\prime} =2\cos x\sin x$$
これは sin 2x と表す事もできます。
また、sin2x を合成関数の微分公式で微分した結果と一致します。
さらに、加法定理・半角の公式でsin2x=(1-cos2x)/2と変形してからxで微分しても同じ結果です。 - y=xex【xと指数関数の積、eは自然対数の底】を微分すると次のようになります。 $$\frac{d}{dx}(xe^x)=(x)^{\prime}e^x+x(e^x)^{\prime}=e^x+xe^x=e^x(1+x)$$ 微分公式 (ex)’ = ex を使っています。
- y=xlnx【xと、eを底とする対数関数の積】の微分を考えます。 $$\frac{d}{dx}x\ln x=(x)^{\prime}\ln x + x(\ln x)^{\prime}=1\cdot \ln x + x\cdot \frac{1}{x}= \ln x + 1$$ これを変形して両辺を積分すると、対数関数についての積分のほうの公式が得られます。$$\ln x = \left(\frac{d}{dx}x\ln x \right) – 1 なので、$$ $$\int \ln x dx=x\ln x -x+C が得られます。$$
- 積分のほうの「部分積分」の公式は、積の微分公式を変形して
$$f^{\prime}g=(fg)^{\prime}-fg^{\prime}$$の両辺を積分したものです。 - f(x)・{g(x)}-1を、合成関数の微分公式も使って積の微分公式に適用すると商の微分公式が得られます。これについてはこのページで後述する証明の箇所でより詳しく説明します。
2番目の例のように微分の計算方法がいくつかあって、積の微分公式を使う事はその方法の1つであるというパターンもあります。計算結果が合っていればどの方法でも構いません。(入試を受験する場合にはなるべく効率のよい計算方法を考えたり、複数の方法で微分する事で計算結果のチェックをするようにしたほうがいいと思います。)
これらの中で、具体的な関数の微分計算も大事である場合もあるのですが、特に積分のほうの部分積分の公式を得るために使われるという事は覚えておくと便利かもしれません。
続いて、商の微分公式の具体的な計算例です。
- y=(sin x)/x を微分すると次のようになります。 $${\large\frac{d}{dx}\frac{\sin x}{x} =\frac{ (\sin x)^{\prime}x-(x)^{\prime}(\sin x) }{x^2} =\frac{x\cos x-\sin x}{x^2} }$$
- y=(ln x)/x を微分すると次のようになります。 $${\large\frac{d}{dx}\frac{\ln x}{x} =\frac{(\ln x)^{\prime}x-(x)^{\prime}\ln x}{x^2} =\frac{x\frac{1}{x}-\ln x}{x^2}=\frac{1-\ln x}{x^2} }$$
- 正接関数 tan x の微分公式は、じつは商の微分公式により導出されます。$$\tan x=\frac{\sin x}{\cos x}なので、$$
$$\frac{d}{dx}\tan x=\frac{(\sin x)^{\prime}(\cos x)-(\sin x)(\cos x)^{\prime}}{\cos^2x}=\frac{\cos^2x +\sin^2x}{\cos^2x}=\frac{1}{\cos^2x}
$$sin x と cos x の微分公式を用いて丁寧に計算すれば証明できます。
三角比の公式 sin2x+cos2x=1を使用しています。 - 三角関数のマイナー組である余接 (cos x)/(sin x)、正割 1/(cos x)、余割 1/(sin x) 【高校ではこれらを覚える必要なし】の微分公式も、商の微分公式を用いれば証明できます。
具体的な計算例として、余接関数を微分すると次のようになります。$$\frac{d}{dx}\cot x=\frac{d}{dx}\frac{\cos x}{\sin x}=\frac{(\cos x)^{\prime}\sin x-\cos x(\sin x)^{\prime}}{\sin^2x}=\frac{\sin^2 x+\cos^2 x}{\sin^2x}=\frac{1}{\sin^2x}$$
正割のように 1/g(x) の形の場合、f(x) = 1 ですから、f'(x) = 0 であり、公式の項が1つ消えるので計算は簡単になります。
一般的に、 1/g(x) の形の関数の微分は次のようになります。 $$\left(\frac{1}{g}\right)^{\prime}=\frac{0\cdot g-1\cdot g^{\prime}}{g^2}=\frac{g^{\prime}}{g^2}$$これは公式として新たに暗記する必要はありません。
むしろ、商の微分公式でこのような式もすぐに導出できるようにしておくとよいでしょう。
これらの具体例を見てみると積と商の微分公式は、初等関数の微積分という範囲に限って見ると割と重要な公式である事が、何となくつかめるのではないかと思います。
公式の証明
証明の方法は合成関数の微分公式や逆関数の証明方法と大体考え方は似ています。積や商の微分公式の場合、証明は合成関数や逆関数と比較すると比較的容易です。
結論を言うと「隠れている『0』」を加えたりしてあげる事で証明できます。
■ 積の微分公式の証明 ■ 商の微分公式の証明
■ 片方の公式からもう片方の公式を導出するやり方
積の微分公式の証明
積の微分公式の場合、 f(x+h)g(x) - f(x+h)g(x) という「隠れている項」を考える事で、2つの導関数の和の形を作れます。 この考え方自体は、数学の他のところ(大学数学も含め)でも、割とよく使われます。
$$\frac{d}{dx}(f(x)g(x))={\large \lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}$$
$$={\large\lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h} }$$
$$ ={\large\lim_{h \to 0}f(x+h)\frac{g(x+h)-g(x)}{h} }+\lim_{h \to 0}g(x){\large\frac{f(x+h)-f(x)g(x)}{h} }$$
$$ =f(x){\large\frac{dg}{dx} }+g(x){\large\frac{df}{dx}}=f(x)g^{\prime}(x)+f^{\prime}(x)g(x) =f^{\prime}g+fg^{\prime}【証明終り】$$
証明の最後のところは、f(x)をf と略して和の順番を変えて整理しただけになります。
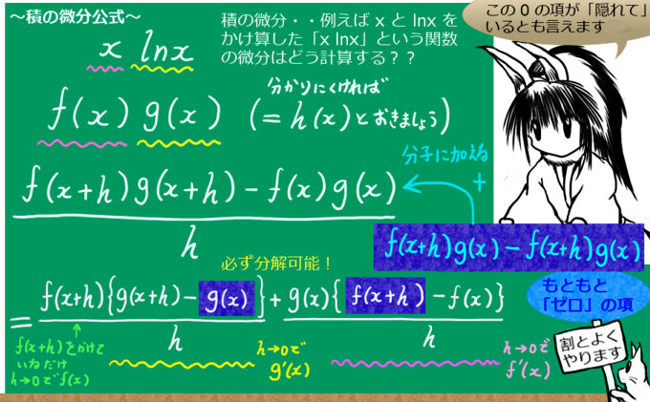
f(x+h)g(x) - f(x+h)g(x) =0という項を加える事で「2つの導関数の和」の形を必ず作る事が可能です。
商の微分公式の証明
商の微分公式も同様の方法で証明できます。
まず分母のg(x+h)とg(x)を通分します。
その後で「-f(x)g(x)+f(x)g(x) (=0)」を分子に加えるという、積の微分公式同様の考え方をします。
$$\frac{d}{dx}\frac{f(x)}{g(x)}={\large\lim_{h \to 0}\left(\frac{f(x+h)}{g(x+h)}-\frac{f(x)}{g(x)}\right)\cdot\frac{1}{h}}$$
$$={\large\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x+h)}{h\cdot g(x)g(x+h)} }$$
$$ ={\large\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x)+f(x)g(x)-f(x)g(x+h)}{h\cdot g(x)g(x+h)} }$$
$$ ={\large\lim_{h \to 0}g(x)\frac{f(x+h)-f(x)}{h\cdot g(x)g(x+h)}}-{\large\lim_{h \to 0}f(x)\frac{g(x+h)-g(x)}{h\cdot g(x)g(x+h)} }$$
$$ ={\largeg(x)\frac{df}{dx}\frac{1}{(g(x))^2}-f(x)\frac{dg}{dx}\frac{1}{(g(x))^2}}$$
$$= {\large\left(\frac{df}{dx}g(x)-f(x)\frac{dg}{dx}\right)\frac{1}{(g(x))^2} = \frac{f^{\prime}g-fg^{\prime}}{g^2}}【証明終り】$$
計算の途中にある分母のところにあるg(x+h)は、h→0でg(x)になるので、これともう1つのg(x)と合わせて公式の分母の2乗を作るわけです。
片方の公式からもう片方の公式を導出するやり方
さて、このように積の微分公式と商の微分公式は、独立に証明できるわけです。
では、片方の公式からもう片方を導出できるでしょうか?
積の公式のほうに1/g(x)としてみると、これは(g(x))-1と考える事ができますから、合成関数のほうの微分公式を使えるのです。計算してみると次のようになります。
$$\frac{d}{dx}\frac{1}{g(x)}=\frac{d}{dx}(g(x))^{-1}=-\frac{dg}{dx}\cdot\frac{1}{(g(x))^2}$$
「g(x)の2乗」というものとマイナス符号が合成関数の微分のほうから出てくるわけで、これを積の微分公式に当てはめると商の微分公式になります。
商の微分公式の第1項はg(x)を「約分」する事もできるわけですが、こちらの証明方法の観点だともともとの1/g(x)の形に由来するというわけです。
他方、商の微分公式のほうが先に証明されているとしましょう。この時に、簡単に前述しましたが 1/g(x)の導関数が今度は合成関数の考え方を使わずに、商の微分公式から導出できるわけです。もちろん結果は同じです。
そのうえで、商の微分公式の中のg(x)を、1/g(x)に置き換えます。ちょっとややこしいですが、微分の部分も含めて丁寧に代入して整理すると積の微分公式になるのです。

つまり積の微分公式と商の微分公式は、独立に証明もできるし、互いに片方の公式からもう片方を導出する事も可能であるわけです。
こういった、証明の方法が複数あるという事については別に知らなくても支障はないし、大学入試の受験という観点からも証明自体が出題される頻度はかなり低いと思いますが、いくつかの方法で試してみる事は計算の練習にはなると思います。
