置換積分の公式

置換積分は「ちかんせきぶん」と読みます。
「置換積分の公式」「置換積分法」とも言い、１変数の積分における公式の１つです。定積分にも不定積分にも、どちらにも使えます。微積分学の基本定理および部分積分と並んで、置換積分は定積分の計算法としてよく使われる公式です。

積分の理論全般について言える事ですが、積分の逆演算である微分のほうについて計算をある程度知っておくと分かりやすくて便利です。また、この記事の説明では三角関数や対数関数の公式なども比較的多く使用します。

公式の内容と意味

置換積分の「置換（ちかん）」とは「置き換える」という意味で、
被積分関数（積分の対象となっている関数）の「積分変数を別の変数に変換する」という事を意味します。つまり置換積分とは、積分における積分変数に対する変数変換を行う時に成立する公式です。

置換積分の公式は不定積分に対しても定積分に対しても成立します。

この式で\(\Large{\frac{dx}{dw}}\)はｘ＝ｇ(ｗ)をｗで微分して得られる導関数を表します。

ここでは変数変換を行う対象をｗとしてますが、文字としてはｔでもｓでも、変数だと分かるもので何かの誤解を生じないものであれば何でも構いません。後述する具体例では、ｘを角度θに変数変換して置換積分を行う場合の計算例を説明しています。

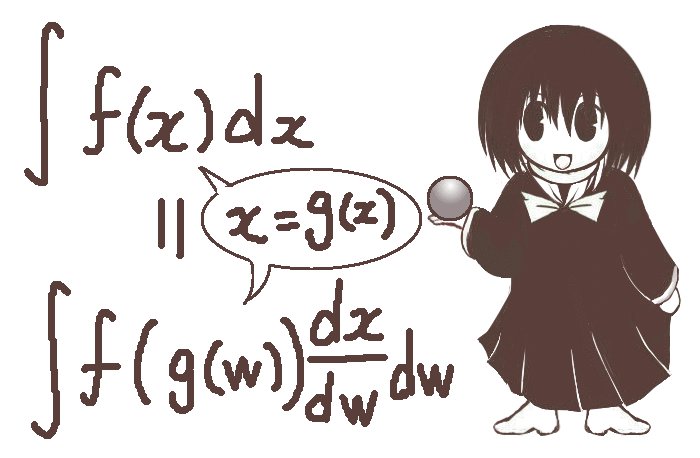
次に、定積分の場合です。
この場合には変数変換をする時に、積分区間も変換される事に注意が必要となります。
その時に普通は２つの端点だけを変換すれば十分で、
例えばｘ＝ｗ＋２のような変換の場合には、ｘに関する [0,1] の閉区間はｗに関する [2.3] の閉区間となって積分区間が変更されるのです。（そうしないと計算の結果は合いません。）

置換積分の公式を適用する時に行う操作を整理し、列挙すると次の事です。

1. ｙ＝ｆ(ｘ)に対してｘ＝ｇ(ｗ)である時、
   ｗで表される式をｆ(ｘ)に代入してｙ＝ｆ(ｇ(ｗ))の形にする。
2. ｘ＝ｇ(ｗ)について、ｘをｗで微分する。
   （なので、微分可能な関数による変換でないと公式は使えません。）
3. 積分の中のｙ＝ｆ(ｇ(ｗ))に対してｘに対するｗによる微分（導関数）を掛け算し、積分変数をｘからｗに変える（ｄｘからｄｗに変える）。それからｗで積分をする。
4. 特に定積分の場合にはｘでの積分区間が [a, b] であったら、
   a ＝ｇ(p)，b=g(q) となるようなｗ＝ｐとｗ＝ｑを見つけて、積分区間を [p, q]に変更する。
   一応、不連続点が発生するような変換をしていないかどうかに少し注意。
5. 不定積分の場合は、ｗで出された結果をｘに戻す事も多い。
   （定積分であれば結果は基本的には数値の事が多いです。）

ただしこの手順の２番目でｘ＝ｇ(ｗ)と考える事については、後述する具体例で見るようにｗ＝ｈ(ｘ)の形で置き換えをしてから、その逆関数としてｘ＝ｇ(ｗ)を考えるような場合もあります。（微分については、公式ｄｗ／ｄｘ＝１／（ｄｘ／ｄｗ）を使えます。）ただしそのような変数変換のパターンでも、逆関数を考えずに積分を計算できるといった場合もあります。それらの事については、具体例を見たほうが多分分かりやすいでしょう。

公式の証明

置換積分の公式は、覚え方や理解の仕方としては「ｄｘ＝(ｄｘ／ｄｗ)ｄｗ」と考える事に差し支えはないけれども、それを数学的な証明とする事はできません。ですのであのような公式が成立する事は自明な事であるとは言えず、証明が必要となります。

証明は、微積分学の基本定理および合成関数の微分法などの微分の演算を組み合わせる事で行えます。（これは数学の解析学的に見た場合も同じで、極限や積分の大元の定義に戻って考える必要はありません。微分の演算等を利用して「解析学的に見ても厳密な証明」になっています。）

最初に不定積分のほうの置換積分の公式を証明します。

まず、「微分すればｆ(ｘ)になる」という意味でのｆ(ｘ)の「原始関数」を考えます。この原始関数自体は、任意定数（微分すると０）を加える事で一意的に定まらず無数に存在しますが、そのうちの特定の１つをF(ｘ)とおきます。原始関数全体が不定積分に該当します。（不定積分は、１つの原始関数があった時にはそれに定数を加えたF(ｘ)＋Ｃの形しかとり得ないという定理があります。）

$$Cを任意の実数定数として\int f(x)dx=F(x)+C$$

$$この時、\frac{d}{dx}\int f(x)dx=\frac{d}{dx}\left(C+F(x)\right)=f(x)が成立$$

今、ｘ＝ｇ(ｗ) がｗで微分可能とすると f(x) の原始関数Ｆ(ｘ) はｗでも微分可能で、合成関数の微分公式により F(ｘ) をｗで微分して得られる導関数は次のように書けます。

$$\frac{d}{dw}F(x)=\frac{dF(x)}{dx}\frac{dx}{dw}=f(x)\frac{dx}{dw}=f(g(w))\frac{dx}{dw}$$

という事は、最右辺の形の関数に対するｗに関する原始関数の１つはＦ(ｘ)である事になります。あるいは、微分方程式を解くと捉えてｗで積分すると考えても同じです。

$$Cを任意定数として、\int f(g(w))\frac{dx}{dw}dw=F(x)+C$$

$$\int f(x)dx=F(x)+Cであったから、\int f(g(w))\frac{dx}{dw}dw=\int f(x)dx$$

定積分の場合は、「不定積分の場合とほぼ同じ」としてもそんなに問題はないのですが、積分区間に関して「端点の部分だけ対応させればよい」事を明確にするために次のような形で証明を行います。

ｘ＝ｇ(ｗ)のもとで、ｇ(ｐ)＝ ａ でありｇ(ｑ)＝ ｂであるとして、Ｆ(ｘ)を先ほどと同じくｆ(ｘ)の原始関数の１つであるとします。Ｆ(ｘ)をｗの関数として見る（ｗだけの式で書く）事を強調するならＦ(ｘ)＝Ｆ(ｇ(ｗ))です。不定積分の時の結果は得られているというもとでｗに関してｆ(ｇ(w))(ｄｘ／ｄｗ)の定積分を計算すると次式になります。

$$\int_p^qf(g(w))\frac{dx}{dw}dw=\large{[F(g(w)) ]}_p^q=F(g(q))-F(g(p))$$

$$=F(b)-F(a)=\int_a^bf(x)dx=\int_{g(p)}^{g(q)}f(x)dx$$

つまり、定積分を行う時には不定積分の時の結果と合わせて、積分区間の端点についてだけｘとｗとで対応させれば確かに同じ計算結果を得るという事が言えるわけです。

計算例１：円と楕円の面積計算

おそらく、置換積分が「計算に有効な事もある」という事が非常に分かりやすい例の１つは
円や楕円の面積を定積分で計算する場合ではないかと思われます。

円の面積に関しては平面幾何的な考察で「半径^２×円周率」という事が分かるほかに、積分を使うにしても実は円周の長さを表す「半径×２×円周率」の式で半径ｒに関して積分すればよいという方法もあるのですが、ここでは直交座標上でｘに関して積分する場合を見てみます。

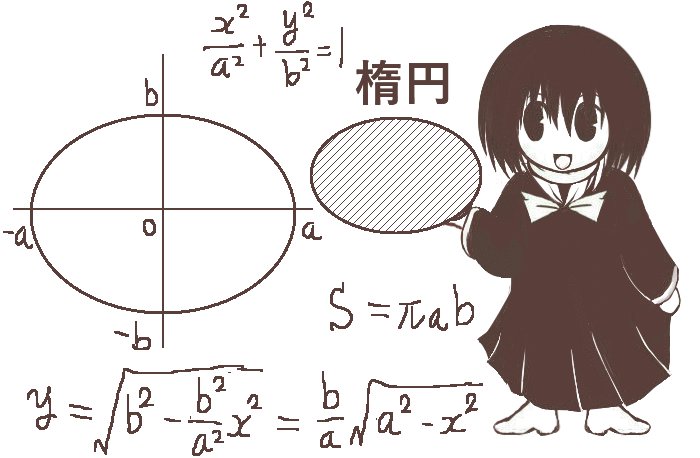
原点を中心とする円を考えて、半径はｒであるとします。（ｒ＞０）
そして、ｘとｙがともにプラスの範囲における４分円（円の１／４の部分だけ考えたもの）の面積についてだけ考えてみます。円全体の面積はその４倍です。

円を表す式はｘ^２＋ｙ^２＝ｒ^２です。ｙについて解くとｙ≧０のほうの解は\(y=\sqrt{r^2-x^2}\)となります。これをｘに関して０からｒまで積分すれば「πｒ^２／４になるはず」ですが、実際のところは一体どうなのだろうという話です。

そのタイプの関数の不定積分は実は直接的に逆三角関数を使っても表せるのですが、置換積分を使うと計算がより簡単であり、「角度」を使って積分できるようになるので図形的なイメージがしやすくなる利点があります。
（参考：逆三角関数を使う方法は、部分積分による計算です。）

そこで、ｘ＝ｒcosθという変数変換をします。ｒは定数（円の半径）でθは変数です。この変数変換は「極座標変換」でもありますが、置換積分を行うという積分の計算だけに着目する場合には、変数変換は図形的な意味を持つ必要は必ずしもありません。
例えば、ここでの計算ではｘ＝ｒsinθとする事も可能で、同じ積分の結果を得ます。（ただし、図形上の考察であれば図と対応させたほうが分かりやすい場合というのはあります。）

この変換のもとで置換積分を考えると、三角関数の公式 sin^２θ＋cos^２θ ＝１により平方根を除いて計算できるようになるので積分の見通しが良くなるのです。積分区間はｘについて の[0,ｒ]をθについての [π／２，０]に変えます。数の大小について一見妙に見えるかもしれませんが、余弦が０から１に増える時は角度は小さくなっていきます。それをそのまま公式に当てはめて計算します。

$$x=r\cos\theta および\frac{dx}{d\theta}=-r\sin\theta を置換積分の公式に当てはめると、$$

$$\int_0^r\sqrt{r^2-x^2}dx=\int_{\large{\frac{\pi}{2}}}^0\sqrt{r^2-r^2\cos^2\theta}\frac{dx}{d\theta}d\theta$$

$$=\int_{\large{\frac{\pi}{2}}}^0r\sin\theta(-r\sin\theta)d\theta =-r^2\int_{\large{\frac{\pi}{2}}}^0\sin^2\theta d\theta=r^2\int_0^{\large{\frac{\pi}{2}}}\sin^2\theta d\theta$$

$$=r^2\int_0^{\large{\frac{\pi}{2}}}\frac{1-\cos 2\theta}{2}d\theta（加法定理か倍角の公式より）$$

$$=\frac{r^2}{2}\large{\left[\theta -\frac{1}{2}\sin 2\theta\right]_0^{\large{\frac{\pi}{2}}}}=\frac{r^2}{2}\cdot\large{\frac{\pi}{2}}=\frac{\pi r^2}{4}$$

つまり、確かに円の４分の１の面積を表す結果となりました。（最後の部分で原始関数に値を代入する箇所では、１次式の θ にπ／２を代入した項以外は全て０となります。）
途中計算での sin^２θの積分を行う時には余弦関数の加法定理を変形して（もしくは倍角の公式を適用）計算を行っています。

楕円の場合も同様に原点を中心としてｘ≧０，ｙ≧０の範囲で全体の１／４を考えて計算できます。
楕円を表す式はｘ^２／ａ^２＋ｙ^２／ｂ^２＝１です。ａもｂもプラスの数であるとします。この式をｙについて解くとｙ≧０のほうの解は次のようになります。

$$y=\sqrt{b^2-\frac{b^2x^2}{a^2}}=\frac{b}{a}\sqrt{a^2-x^2}$$

この式の形を見ると、円の時の式でｒ＝ａとして全体をｂ／ａ倍にしたものになっています。
ですので円の場合と同様に置換積分で計算する事ができますが、
楕円（の４分の１）において積分する区間もｘについて[0, a]なので
「半径ａの円の、積分によって導出した面積のｂ／ａ倍」を考えても同じ結果になります。

$$楕円全体で計算すると、4\cdot\frac{\pi a^2}{4}\cdot\frac{b}{a}=\pi ab$$

これが楕円の面積を表す式になります。図形的には、２ａおよび２ｂはどちらが長いか短いかで「長径」と「短径」を表します。また、ａ＝ｂであれば円になりますが、面積の式もきちんとそれに対応している事が分かります。さらに円を「縦や横の一方向にだけ拡大縮小した場合」にはその倍率の分だけ面積も増加または減少する事が、数式的に見れるわけです。（ａ＝ｂの状態から例えばａ＝２ｂとすれば面積もａ＝ｂの時の２倍になります。）

計算例２：物理・電磁気学での使用例

物理での計算で、考察の対象によっては置換積分が計算に使える事があります。

例えば電磁気における特定の場合などです。ここでは電気のほうで例を見てみましょう。
静電気力と電場に関する１つの計算例です。
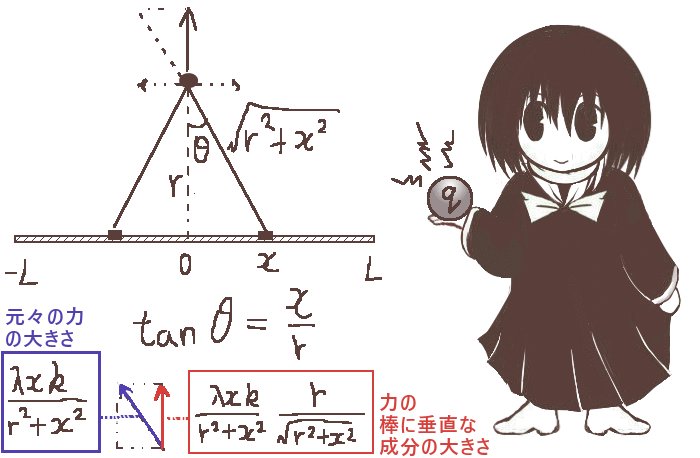
長さが２L[m]の直線状の棒が、線密度λ[C／ｍ]で一様に帯電している（１ｍあたりの電荷がλ[C]）とします。この棒の中心から棒に対して垂直にｒ[ｍ]の位置において、電場の大きさ（１[C]の電気量の電荷が受ける力）はいくらになるでしょうか。

棒の中心を原点にとり、そこからの距離を向きを含めてｘ[ｍ]とします。それぞれの微小な区間における電気量はλｄｘ[C]で、電場を考える位置までの距離は三平方の定理を使って(ｘ^２＋ｒ^２)^１／２[ｍ]です。クーロン力が働くと考えるとそれの逆２乗に比例するので(ｘ^２＋ｒ^２)^－１が式に乗じられます。

棒に帯電している電荷が対称的な分布である事を考えると、棒の中心を通る垂線上では電場のベクトルの「合計」の向きは棒に対して垂直です。（棒の平行な向きの成分はプラスマイナスで打ち消して０です。１つ１つの電場ベクトルの向きは基本的に斜め方向。）そこで、成分の比率を考えると棒に対する垂直方向成分の割合は図形的な関係からｒ／(ｘ^２＋ｒ^２)^１／２になります。比例定数をｋとすると、電場は微小区間による帯電が作る電場（ベクトル）の合計なので、棒に対する垂直成分の合計は積分で考える事ができて次のようになります。（ここで変数はｘのみです。）

$$E=\int_{-L}^{L}\frac{k\lambda}{(x^2+r^2)}\frac{r}{\sqrt{x^2+r^2}}dx=k\lambda r\int_{-L}^{L}\frac{1}{\large{(x^2+r^2)^{\frac{3}{2}}}}dx$$

それで、この積分は原始関数を探す事で計算できるのかという話なのですが、
これは実は置換積分を行う事で計算できる部類の式です。

図で、ｘ＝ｒtanθとなるように角度θをとります。棒の端点ではθ＝θ_Lおよび－θ_Lであるとします。これはｘ＝Ｌとｘ＝－Ｌに対応するわけです。すると、ｄｘ／ｄθ＝ｒ／cos^２θである事を使って置換積分を行うと次のようになります。

$$\frac{dx}{d\theta}=\frac{d}{d\theta}(r\tan\theta)=\frac{r}{\cos^2\theta}であり、$$

$$x^2+r^2=r^2(\tan^2\theta +1)=r^2\frac{1}{\cos^2\theta}にも注意して$$

$$E=k\lambda r\int_{-\theta_L}^{\theta_L}\frac{1}{\large{(r^2\tan^2\theta+r^2)^{\frac{3}{2}}}}\frac{dx}{d\theta}d\theta=k\lambda r\int_{-\theta_L}^{\theta_L}\left(r^2\frac{1}{\cos^2\theta}\right)^{\large{-\frac{3}{2}}}\frac{r}{\cos^2\theta}d\theta$$

$$=k\lambda r\int_{-\theta_L}^{\theta_L}r^{-3}\cos^3\theta\frac{r}{\cos^2\theta}d\theta=\frac{k\lambda}{r}\int_{-\theta_L}^{\theta_L}\cos\theta d\theta=\frac{k\lambda}{r}\{\sin\theta_L-\sin(-\theta_L)\}$$

$$=\frac{2k\lambda}{r}\sin\theta_L=\frac{2kL\lambda}{r\sqrt{r^2+L^2}}$$

電場の大きさの単位は [N／C] になります。最後の変形は図形的に見て正弦を辺の比で表しています。物理的な考察としては、単独の点電荷の場合とは距離の影響が異なってくる事や、L→∞とした場合はどうなるかといった事を見れます。

少し長ったらしい計算ではありますが、このように結果を出せるわけです。一見複雑な積分でも置換積分を行うと、角度θでの積分だと意外と単純な定積分計算に変わった事が分かります。この例では、置換積分で使う変数変換を図の関係にも合わせる事によって、図で平面幾何的に成立する関係も使えるようになっています。（例えば三角関数を辺の比で表す事など。）このように上手く行く事ばかりではないのですが、置換積分の公式を応用計算に使える事もあるという例の１つです。

似た計算は磁場に関しても可能で、ソレノイドが作る磁場や、直線電流が作るビオ・サバールの磁場を具体的に計算する時なども似た感じの積分計算を行います。

計算例３：数学上の色々な不定積分の計算

微分に関しては多少複雑な形の関数であっても、公式を組み合わせて丁寧に計算すれば導関数を計算できるのが普通です。しかし、積分のほうに関してはそれほど複雑でない形の関数に対してでも原始関数の具体的な形を直接見つける事は難しい場合のほうが多いのです。そこで、部分積分や置換積分を使うと原始関数が分かる場合があります。

以下の例はどちらかというと数学上の理論的な計算が中心になりますが、一部は応用にも使えます、

具体的な積分に対して置換積分を使える場合というのは、実際のところは２パターンあります。

• ｘ＝ｇ(ｗ) の形で置き換えをすると式が簡単になる場合
• ｘで表される式についてｈ(ｘ)＝ｗとおいてから逆関数としてｘ＝ｇ(ｗ)を計算して公式を適用するか、もしくはｄｗ／ｄｘを計算した式を使うという場合

前者の場合は公式通りの使い方です。前述の円の面積を積分で計算する方法や、電場の大きさを計算する過程での置換積分の使用においてはこちらのパターンです。すなわち例えばｘ＝ｒcosθ やｘ＝ｒtanθのように変数変換をしたのでした。

他方で後者のほうは、一般的には面倒な形になっているｘの式を別の１つの変数としてしまってから、何らかの方法で置換積分ができるところまで持って行くというものです。
これは例えば、ｗ＝ｘ^２であるとかｗ＝tanｘとする事を指しており、それでもあくまでｘの代わりにｗによる変数変換で置換積分を行うという例です。多少分かりにくいと思うので後ほどｗ＝tan(ｘ／２)とする例などで具体的に説明していきます。

原始関数がいくつかの和や差の項に分離するパターン

まず、「微妙に定数分だけ値がずれた項を含む」関数の原始関数を計算する場合です。
例えば\(x\sqrt{x+2}\) などの積分です。

もしこれが\(x\sqrt{x}\)であれば、平方根の部分はｘ^１／２ですので
全体をｘ^３／２として考えて原始関数は(２／５)ｘ^５／２＋Ｃとなるわけです。

この考え方のみでも一応計算はできて、
それは\(x\sqrt{x+2}=(x+2)\sqrt{x+2}-2\sqrt{x+2}\) とする事で可能になるのです。

$$\int x\sqrt{x+2}dx=\int\{(x+2)\sqrt{x+2}-2\sqrt{x+2}\}dx$$

$$=\int(x+2)^{\frac{3}{2}}dx-\int2(x+2)^{\frac{1}{2}}dx$$

$$=\frac{2}{5}(x+2)^{\frac{5}{2}}-\frac{4}{3}(x+2)^{\frac{3}{2}}+C$$

この積分は実は置換積分で考えてもよくて、ｘ＝ｗ－２と置く事で、置換積分の公式を使えます。
\(x\sqrt{x+2}=(w-2)\sqrt{w}=w\sqrt{w}-2\sqrt{w}\) となります。つまり、若干の違いではありますが「差で表される２つの項に分離する」事が少しばかり自然な形で計算されます。置換積分を行う時にはさらに微分の計算も必要なわけですが、この場合はｄｘ／ｄｗ＝１ですので簡単に済みます。

$$\frac{dx}{dw}=\frac{d}{dw}(w-2)=1に注意して、$$

$$\int x\sqrt{x+2}dx=\int(w-2)\sqrt{w}\frac{dx}{dw}dw=\int(w\sqrt{w}-2\sqrt{w})dw$$

$$=\frac{2}{5}w^{\frac{5}{2}}-\frac{4}{3}w^{\frac{3}{2}}+C=\frac{2}{5}(x+2)^{\frac{5}{2}}-\frac{4}{3}(x+2)^{\frac{3}{2}}+C$$

最後にｗをｘに戻す操作ではｘ＝ｗ－２ ⇔ ｗ＝ｘ＋２を使っています。

置換積分を行う時に、まずｗ＝ｘ＋２とおいてから計算を進めても結果は同じです。
この場合は、どちらの方法で最初に考えてもそんなに手間は変わらないと思います。
他方で、平方根の部分を丸ごとｗに置き換えて\(\sqrt{x+2}=w(\Rightarrow x+2=w^2)\)と考えてもこの場合は計算は可能で、同じ結果を得ます。

いずれにしても、このようなちょっとした初等関数を組み合わせた関数に対してでも、原始関数は結構面倒な形である事が分かります。計算はやりやすい方法でやればよいのですが、２通り以上のやり方を知っておくと片方を検算用に使えるというちょっとした利点はあります。

三角関数に変換すると上手く計算できるパターン

「見事に上手く行く」例は限られていますが、
ｘを三角関数に変数変換すると原始関数が分かり、積分を計算できる場合があります。

例えば、１＋ｘ^２という項が含まれる関数では、
ｘ＝ tanｗと変数変換すると上手く計算できる場合があります。
というのも、(ｄ／ｄｗ)tanｗ＝１＋tan^２ｗ＝１／(cos^２ｘ)といった計算ができるためです。
前述の電磁気学での電場の計算例で使用した変数変換は、このパターンに属する置換積分です。
被積分関数の分母に含まれる式が１＋ｘ^２ではなくｒ^２＋ｘ^２でしたから、変数変換はｘ＝ ｒtanθとする事によって、代入するとｒ^２(１＋tan^２ｗ)のようにできる工夫をしていたわけです。

また、同じく前述の円の面積計算のところで考察した (１－ｘ^２)^１／２などの式の場合は
ｘ＝cosｗとすれば(１－cos^２ｗ)^１／２＝(sin^２ｗ)^１／２＝|sinｗ|などとできます。
【ｗの範囲によっては(sin^２ｗ)^１／２＝sinｗで、前述の例では定積分の積分区間がその範囲です。】

ｘ＝ tanｗと変数変換して上手く行く他の例は、例えば次のようなものです。不連続点が発生しないようにするために－π／２＜ｗ＜π／２の範囲で考えるものとします。（その範囲では cosｗ＞０です。）
(１＋ｘ^２)^１／２＝(１＋tan^２ｗ)^１／２＝{１／(cos^２ｗ)}^１／２＝１／cosｗ
１＋tan^２ｗ＝１／(cos^２ｗ) ⇔ cos^２ｗ＝１／(１＋tan^２ｗ)
およびｄｘ／ｄｗ＝１／cos^２ｗの計算を使います。

$$\int\frac{x}{(1+x^2)\sqrt{1+x^2}}dx=\int\frac{\sin w\cos^3w}{\cos w}\frac{dx}{dw}dw=\int\frac{\sin w\cos^3w}{\cos w}\frac{1}{\cos^2w}dw$$

$$=\int\sin wdw=-\cos w+C=-\frac{1}{\sqrt{1+\tan^2 w}}+C=-\frac{1}{\sqrt{1+x^2}}+C$$

この積分に関しては、計算に慣れていると置換積分を行わなくても直接計算で最後の式を最初から出せるかもしれません。

三角関数による有理関数の積分

ｘをｗによる変数変換で置換積分する時に変数変換として「ｗをｘで表すパターン」には、例えばｗ＝tan(ｘ／２)という形の変数変換があります。
その変換のもとでは
ｄｗ／ｄｘ＝１／{２cos^２(ｘ／２)}＝{１＋tan^２(ｘ／２)}／２＝(１＋ｗ^２)／２により
ｄｘ／ｄｗ＝２／(１＋ｗ^２)
【※普通、逆関数の微分公式を使うと計算後に変数の入れ替えが必要ですが、ここではｄｗ／ｄｘの結果をｘではなく「ｗで表せる」のでそのまま逆数としたものがｄｘ／ｄｗを表す式になります。】
さらに、加法定理や倍角の公式にも注意すると正弦、余弦、正接のいずれをも、
ｗの有理関数（分子と分母が多項式の形の分数で表される関数）で表す事ができます。

そして有理関数は部分分数展開などをする事により、「(別の)有理関数」「lnｘ」「Arctanｘ（逆正接関数）」およびそれらの合成関数のみで表せるという定理が実は存在します。そのため、三角関数の有理関数（つまり三角関数のベキ乗と係数で作られる多項式）は理論上は有限回の操作で原始関数を導出できるという事になるのです。

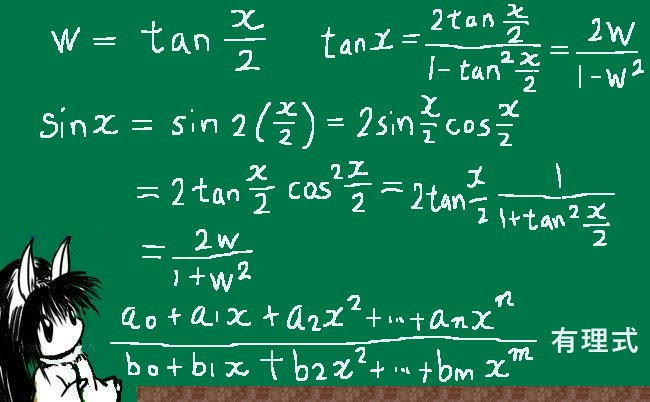
ただし有限回の操作で計算の実行が可能という事と、
その具体的な計算の効率が良いかどうかは別問題ですので一応注意は必要です。
しかし、比較的単純な三角関数の有理関数の積分であれば、
ｗ＝tan(ｘ／２)の形の変数変換による置換積分は積分の計算に活用できます。
例えば１／cosｘ＝(１＋ｗ^２)／(１－ｗ^２)のようになるので、
これはｄｘ／ｄｗ＝２／(１＋ｗ^２)と掛け合わせると
(１／cosｘ)(ｄｘ／ｄｗ)＝２／(１－ｗ^２)＝２／{(１＋ｗ)(１－ｗ)}となります。
この形の式は実は部分分数展開で２項の和に分ける事ができるパターンなので、
原始関数を対数関数と三角関数（最後にｗをｘに戻す）の組み合わせで表す事ができます。

$$\int\frac{1}{\cos x}dx=\int\frac{1+w^2}{1-w^2}\frac{dx}{dw}dw=\int\frac{1+w^2}{1-w^2}\frac{2}{1+w^2}dw$$

$$=\int\frac{2}{(1+w)(1-w)}dw=\int\frac{1}{1+w}dw+\int \frac{1}{1-w}dw$$

$$=\mathrm{ln}\left|1+\tan\frac{x}{2}\right|-\mathrm{ln}\left|1-\tan\frac{x}{2}\right|+C=\mathrm{ln}\large{\left|\frac{1+\tan\frac{x}{2}}{1-\tan\frac{x}{2}}\right|}+C$$

このように、三角関数の逆数を積分すると原始関数には対数関数が含まれて来る事が分かります。
置換積分なしでこの結果を予想するのは少し難しいと言えそうです。

ここで使っている対数は自然対数です。
lnｘ＝log_eｘで、\(\large{\frac{d}{dx}\mathrm{ln}x=\frac{1}{x}}\)であり、
ｘ＜０のとき\(\large{\frac{d}{dx}\mathrm{ln}(-x)=\frac{1}{x}}\)なのでまとめて\(\large{\frac{d}{dx}\mathrm{ln}|x|=\frac{1}{x}}\)とも書きます。

１／sinｘの不定積分も同じように計算できて、計算はより簡単です。

$$\int\frac{1}{\sin x}dx=\int\frac{1+w^2}{2w}\frac{dx}{dw}dw=\int\frac{1+w^2}{2w}\frac{2}{1+w^2}dw$$

$$=\int\frac{1}{w}dw=\mathrm{ln}|w|+C=\mathrm{ln}\left|\tan\frac{x}{2}\right|+C$$

合成関数の利用によっても原始関数が分かるパターン

ある形をしている関数の積分は、原始関数を直接見つける事は可能だけれども、
もし分かりにくければ置換積分を使うとよいという部類のものです。

具体的には、\(\large{xe^{x^2}}\)や、\(\Large{\frac{1}{x\mathrm{ln}x}}\) などの関数です。
あるいは、正接関数 tanｘの原始関数も実は同じ部類のものです。
これらは置換積分で計算する事もできますが、もし合成関数の微分に慣れていると原始関数は直接計算でも導出可能と言える部類の関数です。

１．合成関数の微分を考慮して直接計算で積分する場合

上記の関数の積分を直接計算する時には、例えば次のようにします。

$$\frac{d}{dx}\large{e^{x^2}}=2x\large{e^{x^2}}なので\int\large{xe^{x^2}}dx=\frac{1}{2}\large{e^{x^2}}+C$$

$$\frac{d}{dx}\mathrm{ln}(|\mathrm{ln}x|)= \frac{1}{x}\frac{1}{\mathrm{ln}x}=\frac{1}{x\mathrm{ln}x}なので\int\frac{1}{x\mathrm{ln}x}dx=\mathrm{ln}(|\mathrm{ln}x|)+C$$

正接関数 tanｘについても、実は対数関数を使って原始関数を導出できます。

$$\frac{d}{dx}\mathrm{ln}|\cos x|=-\frac{\sin x}{\cos x}=-\tan xであるから\int\tan x dx=-\mathrm{ln}|\cos x|+C$$

つまり、(ｄｇ／ｄｘ)ｆ(ｇ(ｘ))の形になっている関数は、
合成関数の微分を考える事で原始関数を見つけて積分を直接計算できるわけです。

ところで(ｄｇ／ｄｘ)ｆ(ｇ(ｘ))という関数の形は、変数を取り換えると(ｄｇ／ｄｗ)ｆ(ｇ(ｗ))となり、ｘ＝ｇ(ｗ)とすれば(ｄｇ／ｄｗ)ｆ(ｇ(ｗ))＝(ｄｘ／ｄｗ)ｆ(ｇ(ｗ))です。
つまり、置換積分の公式の「積分の中身」の形になっています。
その事が、置換積分によっても計算が可能である事と関係しています。

２．置換積分を使う場合

直接計算が少し分かりにくければ置換積分を使う事もできます。
ただし、ここでの例のような場合はいずれもｗ＝ｈ(ｘ)の形をまず考えるタイプの計算になります。

例えば、上記の指数関数の例ではｗ＝ｘ^２，対数関数の例ではｗ＝lnｘ、
正接関数の場合はｗ＝cosｘと置きます。

ここでｘ＝ｇ(ｗ)の形の逆関数を考えると、例えばlnｘ＝ｗに対してはｘ＝e^ｗですが、逆三角関数などを考えるのは微分の計算もある事を考えるとちょっと面倒そうです。

このような場合、微分に関してはｘに関して行ったほうが最初の計算は簡単です。

$$\frac{d}{dx}x^2=2x\hspace{15pt}\frac{d}{dx}\mathrm{ln}x=\frac{1}{x}\hspace{15pt}\frac{d}{dx}\cos x=-\sin x$$

すると、ここでの例は「特別な場合」である事は強調される必要はありますが、
ｘでの微分の結果（つまりｄｗ／ｄｘ）が原始関数を導出したい関数の一部に実は含まれています。
例えば\(\large{xe^{x^2}}\)において、ｘはｘ^２の微分を定数係数を乗じた形です。
（※そこまで分かると前述の直接計算も可能になます。）
さらに、逆関数の微分公式によりｄｗ／ｄｘ＝１／（ｄｘ／ｄｗ）ですから、
置換積分を行う時に「掛け算で１にする」事ができます。

上記の指数関数が含まれる例では次のようになります。

$$\large{w=x^2 とおくとxe^{x^2}}=\frac{1}{2}\frac{dw}{dx}e^wなので、$$

$$\int\large{xe^{x^2}}dx=\frac{1}{2}\int\frac{dw}{dx}e^w\frac{dx}{dw}dw=\frac{1}{2}\int e^wdw=\frac{1}{2}e^w+C=\frac{1}{2}\large{e^{x^2}}+C$$

式の途中計算で分かるように、置換積分の公式で使用するｄｘ／ｄｗがｄｗ／ｄｘに乗じられる事で１になって積分計算が簡単になっているわけです。もちろん、この関数はそのようになる「特別な形」をしているのでそのようにできます。

対数関数の逆数が含まれる例では次の通りです。

$$\large{w=\mathrm{ln}x とおくと\frac{1}{x\mathrm{ln}x}}=\frac{dw}{dx}\frac{1}{w}なので、$$

$$\int\frac{1}{x\mathrm{ln}x}dx=\int\frac{dw}{dx}\frac{1}{w}\frac{dx}{dw}dw=\int\frac{1}{w}dw=\mathrm{ln}|w|+C=\mathrm{ln}(|\mathrm{ln}x|)+C$$

正接関数では次のようになります。

$$w=\cos x とおくと\tan x=\frac{\sin x}{\cos x}=-\frac{dw}{dx}\frac{1}{w}なので、$$

$$\int\tan x dx=-\int\frac{dw}{dx}\frac{1}{w}\frac{dx}{dw}dw=-\mathrm{ln}|w|+C=-\mathrm{ln}|\cos x|+C$$

これらの場合においては、置換積分を使ったほうが分かりやすいかどうかは人によって感じ方が違うでしょう。分かりやすいほうで理解したほうがよいと思われます。