座標変換のうち、理論面でも応用面でも良く使われる極座標と、その3次元版である球面座標について述べます。(※3次元の球面座標の事も極座標と呼ぶ事もあります。)
また合わせて、時々使われる円柱座標についても述べます。
極座標(polar coordinates)の「極」とは英語で言うと pole 、
北極とか南極で使う意味での「極」(「一方の果て」「端、両端」)になります。
尚、球面座標は英語だと spherical polar coordinates です。
- 弧度法の考え方と計算
- 三角関数の定義と図形的な三角比の基礎
- 複素数の極形式
- 円を表す式(直交座標)
基本の考え方:三角関数を使う
極座標の発想自体は簡単で、
「平面座標のある点と原点とを結ぶと、必ず『長さと角度(x軸から測った角度)』で表せるはず」
という事なのです。
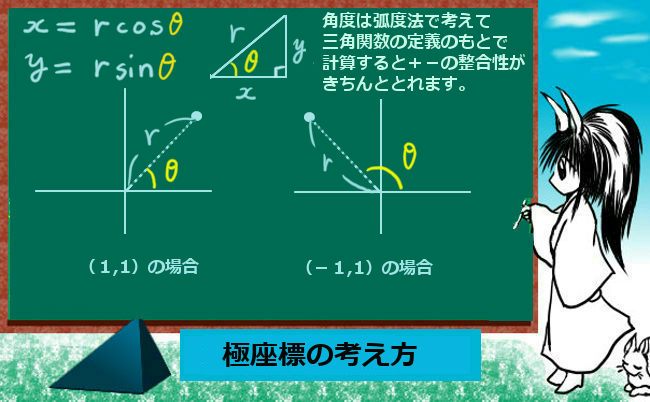
例えば、(1,1)という点は原点からの距離が\(\sqrt{2}\)で角度は\(\pi\)/4(あるいは45°)です。
(-1,1)という点であれば原点からの距離が\(\sqrt{2}\)で角度は3\(\pi\)/4(あるいは135°)です。
図で見ると単純で分かりやすいでしょう。
極座標は、原点を中心とする円と原点を通る直線から構成される曲線座標でもあります。曲線座標のうち、最も簡単で便利でもあるものの1つです。
3次元で球面上の点と見なす場合には、後述しますように、原点からの長さに加えて角度を2つ使用します。
物理学での応用
極座標や球面座標を使う事によって、曲線の概形の把握が容易になる事や、微分方程式の解法が容易になる事があります。例えば、力学では等速円運動の分析において極座標を使うと簡単に中心力が働く事を導出できます。
また、万有引力が働くと軌道として楕円があり得るという理屈は、運動方程式を極座標変換する事で手計算で導出可能です。この時、軌道は条件によって円や放物線でもあり得る事が分かります。
(※運動方程式も含めて、微分方程式を座標変換する時はちょっとした面倒な計算が必要です。)
その他に、量子力学で水素原子の電子軌道の式を導出する時にも、基本の方程式で球面座標への変換が行われる事で手計算が可能となり、相対性理論でも時空の歪みが方向には依存しない(等方である)事を条件に課す時に座標の空間成分の一部が極座標・球面座標の形であると考えて理論が組み立てられます。
それらの微分方程式等を考える時に、強引にxyzの座標で考える事も不可能ではないのですが、手計算で計算を進める事は非常に困難になるのです。
変換方法:極座標
実際に変換をする時には、三角関数(図で直感的に考えるなら三角比)を使用します。図を描いてみると次の三点で必ず直角三角形を作れる事に起因します:
- ある座標の点
- その点からx軸に降ろした垂線の足
- 原点
そこで、原点からある点までの長さをr、x軸から測った角度をθとすると、
三角比の計算というか定義通りに、次の関係が成立します。
- x=rcosθ
- y=rsinθ
※この時に、θの範囲は全実数ですが、rは0以上の実数という事になります。
この時に、座標が負の値であっても正弦と余弦を三角関数として考えれば、正しく関係が満たされるのです。

また、xとyの値からrとθを表す事もできます。
- \(r=\sqrt{x^2+y^2}\)
- \(\cos \theta=\Large{\frac{x}{\sqrt{x^2+y^2}} }\)\(\hspace{10pt}\sin \theta=\Large{\frac{y}{\sqrt{x^2+y^2}}}\)
※逆三角関数を使えば強引に θ=・・・の形にもできますが、一般にはあまりメリットがありません。
高校生の方であれば、これらの関係式は暗記するのではなく、xとyの式を2乗して加えるか、図の三角形の関係から直ちに理解できるように努める事が勧められます。
尚、これらの考え方は複素数の極形式の考え方に直結するものとなります。座標の原点回りの回転を考える時には複素数の極形式を使ったほうが良い場合もあります。(※回転に関しては、特にそれを群と見なす時には行列で考えたほうが良い事もあります。いずれの場合も、回転で基本となっているのは加法定理です。)
特定の関数で表された曲線を、極座標で表された点の集まりとして表示する事もできます。
例えばy=x2を強引に極座標で表すには、x=rcosθとy=rsinθをそのまま代入すればよいのです。
すると、rsinθ=r2cos2θ ⇔ sinθ=r(1-sin2θ) のような関係になります。
そのような関係式を満たすrとθの組み合わせの点の集まりが、y=x2で表される放物線と全く同じものを表すという事です。
尚、半径Rの円の式に極座標変換を当てはめると、r=Rという形の式になります。
(rは座標の目盛で、Rは何かしらの定数です。r=一定の値という事です。)
x2+y2=R2にx=rcosθとy=rsinθを代入すると
r2cos2θ+r2sin2θ=R2
⇔ r2(cos2θ+sin2θ)=R2
⇔ r2=R2 ⇔ (r-R)(r+R)=0
rとRは正の数だからr=R
このように極座標で表す利点があるかないかは、その時々によって異なります。一般的には、円とか球とか、そういったぐるりと1周回るものを考える時や、周期性のあるものを考える時に極座標を使う計算上の利点がある場合が多いかとは思います。
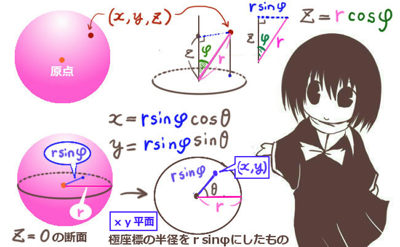
球面座標
次に、球面座標を考えてみましょう。考え方自体は、2次元平面での極座標と同じなのです。
- x=rsinφ cosθ
- y=rsinφ sinθ
- z=rcosφ
半径rは「球の半径」である事と、角度φの取り方に注意。
「sinφ cosθ」は、sinφ と cosθ との掛け算です。
θとφという2つの角度を使いますが、まずz座標から考えてみる事がポイントです。
まず「z軸」「原点」「点(x,y,z)」が作る角度をφとします。
そして、z座標をz=rcosφと表すのです。
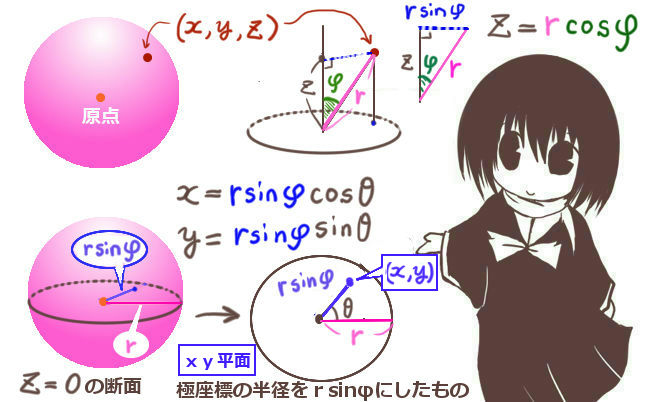
次に、xy平面上で測った角度も必要になります。z=0での平面を考えて、この面でのx軸から測る角度をθとします。「x軸」「原点」「球面上の点からの垂線の足(x,y)」が成す角をθとするという事です。
ここで、先ほどのφを使うと、原点から垂線の足までの距離はrsinφになります。(余弦ではなく正弦になります。)
すると、xとyは、「半径をrsinφと見なした時」の平面の極座標と全く同じ考え方で表す事ができるというわけです。つまり、半径であるrsinφに、それぞれcosθとsinθを掛ければよいという事です。
x=(rsinφ) cosθ =rsinφ cosθ, y=(rsinφ) sinθ =rsinφ sinθ という事になり、球面座標への変換の式が完成するわけです。暗記しようと思うといかにも面倒な式ですが、図で見ると非常に単純なものを意味する式である事が分かるかと思います。
円柱座標
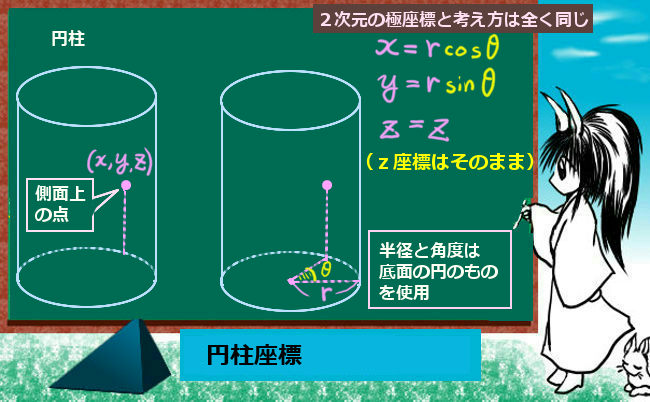
最後に、円柱座標についても見ておきます。これは、3次元空間の点を円柱の側面として座標を考えるという事ですが、実は発想は非常に単純です。
まず、円柱には必ず底面となる円がありますから、底面がxy平面上にあるとすればxとyについては極座標と全く同じ式を使えます。
ではz座標はどうするのかというと、実は「何も変換しないでそのままzの値を使う」というふうにします。z=zとするのです。この単純な発想を受け入れると、円柱座標は次のようになります。
- x=rcosθ
- y=rsinθ
- z=z
z座標を無視すると、普通の平面での極座標と全く同じ形です。
場合によってはz=hなどのように置き換えはしますが、意味は同じです。
実に単純である事が分かると思います。
このように、図も使ってシンプルに捉えれば難しいものではない事が理解できるでしょう。