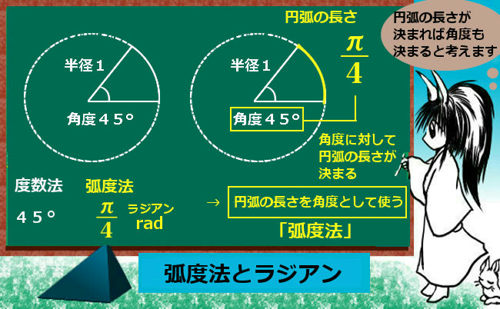
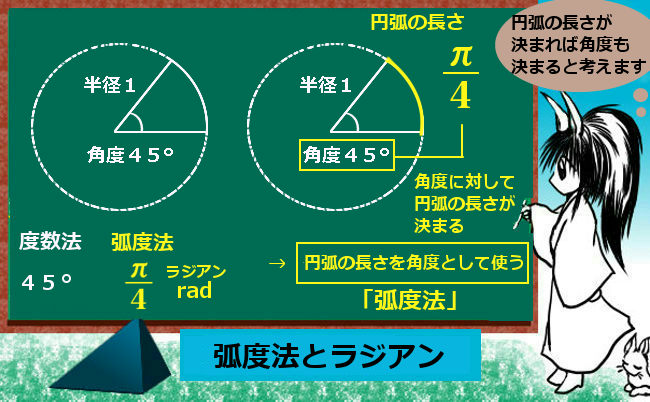
弧度法とは、半径1の円の円弧の長さ(扇形の周部分)によって角度を表す方法を言います。
基本的には、円周率の有理数倍によって使って表す事が多いです。
弧度法で表した角度には単位をつけない事も多いですが、「ラジアン」[rad]という単位を記す事もあります。(英:radian)
定義・考え方と重要ポイント
弧度法は次のように定義され、度数法との換算の仕方も合わせて記すと次のようになります。
半径1の円の円弧の長さが Y 、その円弧を得る扇形の中心角の大きさが度数法で X ° である時、
円弧の長さ Y を角度そのものとして扱う方法を弧度法と言い、
特に単位をつける場合には rad (ラジアン)を使う。
Y [rad] と X [°]の換算については次の関係が成立する:
$$Y=\frac{\pi X}{180}=\frac{2\pi X}{360}$$
この角度の表し方の詳しい意味と、換算の式の出し方についての易しい説明を以下にしていきます。
円周の長さは直径と円周率の積です。この時に半径(および直径)が一定であれば円周の長さも一定です。
(円周の長さ)=(直径)×(円周率)という事です。
まず、簡単な例として「半円」を考えてみましょう。これの「弧」の長さを考えます。
当然ながら、半円の弧の長さは「全体の円周の長さの半分」です。
1/3円であれば弧の長さも1/3です。1/n円であれば弧の長さは全体の1/nです。
ところで一般の扇形の面積や円弧部分の周の長さを考える時は、例えば中心角が60°の扇形は、
全体に対して60/360=1/6 の割合の面積や弧の長さを持つと判定するのでした。
全体を360°として、60°という部分を考えています。
これは、角度が分かっているので円弧の長さも分かるというわけです。
そこで、弧度法の基本的な考え方は次のようなものです。
「逆に、『弧の長さ』が仮に分かってるとすれば『角度』も確定するではないか?」
半径1の円の60°の扇形の弧の長さは\(\pi\)/3ですが、言い換えると弧の長さが\(\pi\)/3であれば
角度も「全体を6分割する」大きさである事は確定しているというわけです。
度数法の場合は360°に対して何度を比較しますが、弧度法では半径1の円の全体の円周の長さ2\(\pi\)に対して、扇形の弧の長さを比較するのです。
この観点では角度を「全体の何割なのか」という視点だけで考えているとも言えます。
換算の式の考え方と導出
弧度法と度数法の換算については、冒頭で記しましたように一応の「公式」はありますが、
基本的には部分が全体の何割かという事を考えているだけなのです。
例えば直角であれば全体の1/4ですから度数法であれば90°、
弧度法なら2\(\pi\)の1/4の\(\pi\)/2であるというわけです。
360/4=90、2\(\pi\)/4=\(\pi\)/2という計算です。
(あるいは半円の半分と考えて180/2、\(\pi\)÷2)
そもそも度数法にしても360という数字について、数学的に絶対にこの値でないと支障があるのかというとそうではありません。例えば極端な話、倍の数字の720を全体としてもよいのです。角度を測るツールとしては何でもよいわけです。その事に気付くと、弧度法というのは全然難しいものではないのです。
とすると、弧度法と度数法の換算も、全体の何割かを把握している事が本質であるわけです。この時、必要に応じて直角や2直角の何割かという事を考えたほうが計算は早い場合はあります。
例えば30°であれば、2直角180°の1/6ですから、弧度法だと半径1の半円の弧の1/6、つまり\(\pi\)/6に等しい角度という事です。
同じく45°なら2直角の1/4なので、弧度法だと\(\pi\)/4です。
前述の90°なら直角ですから弧度法では\(\pi\)/2と直ちに考える事もできます。
120°のような場合は、2直角の2/3ですから(60°の2倍)、弧度法では2\(\pi\)/3なのです。
このように考えると、じつに簡単なものである事に気付くと思います。
37°のような半端な角度の場合も考え方は同じなのです。要するに、全体の何割かを考えればよいのです。90°未満の角度の場合は180°に対する割合を考えたほうが簡単でしょう。
すると、この角度を弧度法で表すなら \(\pi\) の37/180倍です。$$37°は、弧度法では\pi\cdot\frac{37}{180}=\frac{37\pi}{180}になります。$$
これが、弧度法と度数法の換算の式の意味です。改めて記すと次のようになります。
$$Y=\pi\cdot \frac{X}{180}=\frac{\pi X}{180} $$ $$もちろんこれは Y=\frac{2\pi X}{360}としても同じです。$$ 逆に弧度法で表された角度 Y [rad] によって度数法の X ° は次のように表されます。
$$X=180\cdot \frac{Y}{\pi}=\frac{180Y}{\pi}$$ $$これはX=360\cdot \frac{Y}{2\pi}=\frac{360Y}{2\pi}としても同じです。$$

この考え方が分かっていると、仮に次のような意地の悪い問題が大学入試(センター試験等)で仮に問われたとしても迷わないでしょう。
■問い:「弧度法の1ラジアンを度数法で表すならいくらか。」
そもそも円周率は無理数なのだから弧度法の角度をわざわざ有理数である「1」で表す意味があまり無いとも言えるのですが、この手の問題では理解度を試すためにわざと問うているという事でしょう。
1ラジアンですから、2直角に対する割合は1/\(\pi\)です。
したがって解答は、180×(1/\(\pi\))=180÷\(\pi\) ≒ 57.3 [°] です。【解答】
考え方としては\(\pi\)/4ラジアンが2直角\(\pi\)に対する1/4、
あるいは直角の半分だから「45°」と判定する事と同じなのです。
一般の円の円弧の長さ・扇形の面積との関係
さて、弧度法で表した角度は「半径1」の円の円弧の長さです。
あくまで半径1の場合ですから、別の半径であれば円周の長さも面積も変わります。
しかし、円周の長さは「半径(あるいは直径)に比例する」のでしたから、
仮に弧度法で表された角度が分かっているのであれば、一般の扇形の円弧の長さは「弧度法の角度[rad]を半径倍したもの」という事になります。
これは、「半径Rの扇形の円弧の長さ」=「『半径1の扇形の円弧の長さ』× R」という簡単な関係なのです。
この意味において、次の公式が成立します。
円弧の長さ L は次のように表されます。
$$L=R\theta$$ ★基本的には角度 θ [rad] は、例えば\(\pi\)/4のような形で判明しているという事に注意しましょう。
つまり、決して「円周率が消えている」という事ではありません。
弧度法での角度があらかじめ分かっているとは、基本的には、あくまで全体に対する何割の扇形であるかが判明しているという意味です。確かに仮に弧度法の角度を無理やり有理数で表せば見かけ上円弧の長さから円周率が消えますが、これは円周全体に占める比を有理数で表せないという「長さ」になってしまうのです。
面積についても考え方は同様です。
半径1の円の面積は1×1×\(\pi\)=\(\pi\)で、
弧度法の角度が θ であれば θ/(2\(\pi\)) の割合が扇形の面積です。
$$半径1の扇形の面積:\pi\cdot\frac{\theta}{2\pi}=\frac{\theta}{2}$$
ここで1/2というのが出てくるのは、円周の長さは直径と円周率との積、円の面積は半径の2乗と円周率との積で、弧度法の角度は円周と円弧の関係を表すものなので直径と半径のずれがあるためです。
扇形の半径がRに変わった時には面積はさらにR2倍になります。
その意味において次の関係式が成立します。
扇形の面積 S は次のように表されます。
$$S=\frac{R^2\theta}{2}$$ ★ここで再び、円周率は基本的には弧度法で表された角度に含まれているのです。
分母の2がつくのかつかないのか分からなくなった時には、半径1の2\(\pi\) [rad] を考えてみるとよいでしょう。この時の扇形は円そのものですから、面積は\(\pi\)です。上記の式に代入しても同じ結果になる事が分かります。
三角関数の変数としての角度は弧度法で表すのが基本です。特に三角関数の微積分を考える時には、度数法を使うと問題が発生するので必ず弧度法の角度を変数として扱います。