正弦定理は、三角形の辺の長さおよび外接円の半径(あるいは直径)と、三角比の正弦の間に成立する関係式です。(英:sine rule)
三角比を使うという事で高校で教えられる事が多いですが、内容としてはどちらかというと平面の図形問題の色彩が濃く、中学校で教わる平面幾何の内容に近いかもしれません。
定理の内容
定理の内容は次の通りです。
三角形ABCでBC=a、AC=b、AB=cとして、
それらの対角の大きさについて∠BAC=A、∠ABC=C、∠ACB=Cとします。
また、△ABCの外接円の半径をRとすると、次の関係式が成立します:
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$
このように1つの式で表されていますが、2つのグループに分かれていると考える事もできます。1つは辺の長さと正弦の関係、もう1つは辺の長さと正弦と外接円の半径の関係です。(後者については証明を見ると分かるように図形上の意味として肝心なのは「直径」との関係です。)
ここでは2つの部分に分けますが、2つ目のほうを使って最初から全て証明する事も可能です。
証明①:三角形の辺と正弦に関する部分
まず、1つ目の辺の長さと正弦の関係です。
定理の中で言うと、とりあえず外接円の部分は無視した次の部分になります。
$$まずこれを証明します:\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$
2つの等号に関して一度に示す事はできないので、1つずつ証明して最後に全部を結ぶという形になります。
これは、一言で言うと、三角形ABCの「面積」を3通りの方法で表してみると成立する事が分かる関係式です。本来の「面積」の形の等号関係は次のようになります。
$$\frac{bc\sin A}{2}=\frac{ac\sin B}{2}=\frac{ab\sin C}{2}$$
発想はじつに単純で、三角形の面積「底辺×高さ÷2」において、底辺を辺AB、BC、ACのそれぞれとした場合に面積の計算をしてみようという、それだけのものです。
★細かい事を言いますと、厳密にはその場合に「どの辺を底辺にとったとしても1つの三角形の『面積』は1つの値しかとらない」という事も自明ではなく要証明です。
しかしその事は平面幾何で証明済のものとして、ここでは話を進めます。
(三角形の相似関係を使えばよく、証明するとしてもそれほど難しくはありません。)
また、証明の順番は逆になってしまいますが、正弦定理の後半部分を先に証明すればこの面積に関する事項も証明する事はできます。どの方法でも間違いではありません。
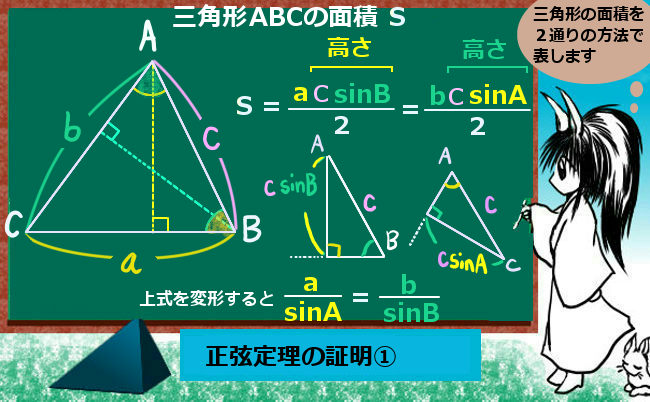
まず。底辺をAC=aとした時です。面積を出すには高さが必要ですが、これを三角比の関係を使って表します。AB=cの斜辺と∠ABC=Bの正弦によって、高さはcsinBになります。これで、面積の1つが表されるわけです。
$$S=\frac{ac\sin B}{2}$$
この時、∠ABC=Bとは逆側の角度を使って、高さの部分をbsinCと表す事もできます。
これは、あとで使います。
最初からそちらのほうだけで面積を表すとどうなってしまうのかというと、じつはa(bsinC)÷2=b(asinC)÷2の関係により、「bを底辺とした場合に表わした三角形の面積」に等しい事になります。そのため、最初からこちらの式を使って進めても結局証明はできます。
底辺をAC=bの部分とみなす場合には、高さがcsinAになります。これで面積の2つ目の表し方です。
$$S=\frac{bc\sin A}{2}$$
ここで、いったん2つの式を等号で結びます。
もちろん、同じ面積Sを表すので等号で結べます。
$$\frac{ac\sin B}{2}=\frac{bc\sin A}{2}$$
この式で、両辺でcと1/2は共通しているので掛け算割り算で「消せる」事になり、さらに正弦の部分を両辺で割ると正弦定理の関係式の1つになります。
$$\frac{ac\sin B}{2}=\frac{bc\sin A}{2}\Leftrightarrow a\sin B=b\sin A$$
$$\Leftrightarrow\frac{a}{\sin A}=\frac{b}{\sin B}$$
ここでもう1つ関係式がほしいわけですが、∠ACB=Cに関する正弦が足りないので、再びBC=aを底辺とする場合に戻って、高さを今度はbsinCと考えます。
$$するとS=\frac{ab\sin C}{2}とも表せる事により、\frac{ab\sin C}{2}=\frac{bc\sin A}{2}$$
$$\Leftrightarrow\frac{a}{\sin A}=\frac{c}{\sin C}$$
これで2つの等号関係を結べます。
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}【証明終り】$$
理解の仕方としては、図を見てもっと単純に直観的にという事でもよいと思います。
証明②:外接円に関わる部分
次に、正弦定理の内容のうち、外接円の半径を含むほうの部分です。
一体どこから円が関係するのかと思われるかもしれませんが、じつはこの後半部分のほうが、図形的な特徴に気付くと直ちに証明されるので簡単なのです。
この場合には面積を考える必要はなく、三角比の関係だけを使います。
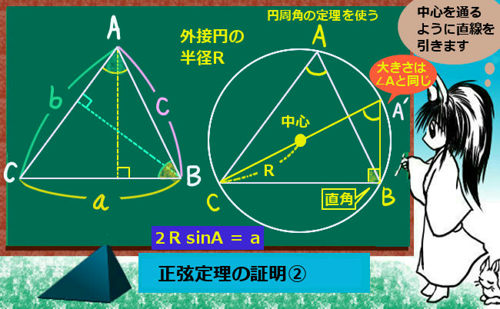
まず外接円を考えるのですが、この時に三角形の1つの頂点から「円の中心を通るように」直線を引きます。それが円周の向かい側とぶつかる点に注目します。
図では、点Cから中心に向かって直線を引き、円周との交点をA’ としています。
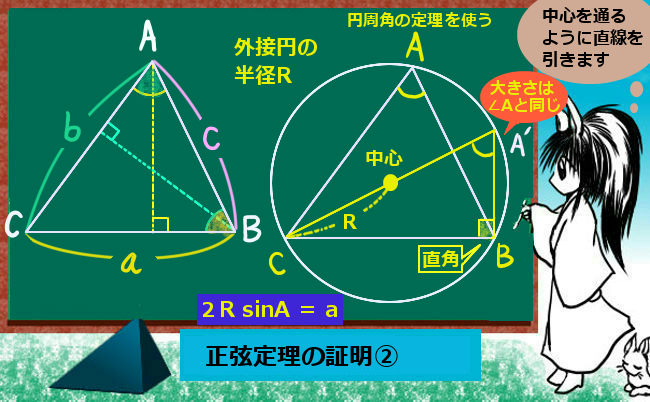
すると、まず円周角の定理により、新しくできた図の∠CA’Bの大きさは∠CAB=Aと同じ大きさです。(弧CBの円周角なので。)よって∠CA’B=Aです。
また、図のCA’ は円の直径ですから、その円周角について∠A’BC=90° となります。(これも本質的には円周角の定理によるものです。)
という事は、Aという大きさの角を含む直角三角形を考える事ができます。斜辺は円の直径(2R)で、辺BCの長さがaですから両者を三角比の関係で結べます。じつは、これで1つの関係の証明が終りです。
$$三角比の関係により、2R\sin A=a\Leftrightarrow \frac{a}{\sin A}=2R$$
同様にして、頂点Aや頂点Bからも補助線を中心に向かって引く事で残り2つの関係式も得られますが、a/(sinA)=b/(sinB)=C/(sinC)を既に証明しているので、これで正弦定理の証明完了としても可です。
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}と合わせて、\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R【証明終り】$$
★こちらのほうの定理の後半の内容について最初に証明する事で前半部分も一度に証明する事もできます。
その場合には頂点と中心を通る補助線を3パターン全て作って、
a/(sinA)=2Rかつb/(sinB)=2RかつC/(sinC)=2Rよりa/(sinA)=b/(sinB)=C/(sinC)であるとして、定理の前半部分もまとめて証明できます。
手間としては、どちらの方法でもあまり変わらないと思います。
この記事では証明を詳しく記しましたが、理解としてはもっと直感的でよいと思います。
さてこの「正弦定理」、別途に「余弦定理」というものがあるので対として教科書の中で教えられる事も多いのですが、大学入試での出題の可能性を除くと重要度はやや低いものがあるかもしれません。
証明の方法から見ても分かる通り、正弦定理とは本質的には三角形の面積に関する平面幾何の基本事項や、円周角の定理から直結する関係式です。そのためこの定理は直接的というよりは、三角形に関わる多くの事項と間接的に関わっているものと言えるかもしれません。