接線線積分は曲線を積分経路とする積分で、
ベクトル場(座標成分を変数とするベクトル関数)に対して定義されます。
目次
☆接線線積分の事を、ベクトル場に対する「線積分」と呼ぶ事もあります。
これに対して、スカラー場(座標変数を変数とするスカラー関数)に対する「線積分」の定義も別途に存在します。
その場合には積分の仕方および積分の方向に対する定義の仕方が、ベクトルに対する接線線積分とは少し異なります。
「ベクトル場に対する接線線積分」と「スカラー場に対する線積分」のいずれも、積分経路を平面または空間内の曲線とする定積分という事は共通します。また、後述しますように、両者は座標成分による内積計算によって関連し合っています。
☆サイト内リンク:参考・より初歩的な内容
接線線積分の英名は、 curvilinear integral と表記される事が多いです。
(「線積分」は line integral 。ただし英名表記でもこの語が接線線積分を指す事もあります。)
ベクトル場に対する接線線積分は、曲線が開曲線である場合と、閉曲線である場合とで、基本的な考え方は同じですが表記方法や積分方向に関する定義が微妙に異なります。

開曲線に対する接線線積分
【定義・考え方・表記方法】
まず、積分経路が閉じていない曲線(開曲線)の場合を考えます。
開曲線とは、図形的には単純に両端がどこにも結び付けられていない曲線の事で、例えば2次関数のグラフのような曲線です。(曲線と言いますが直線も含みます。)
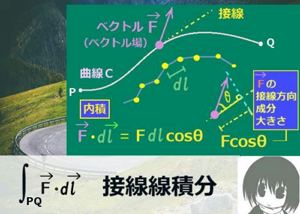
そこで、ベクトル場を\(\overrightarrow{F}\)として、
ある曲線の点Pから点Qまでの接線線積分を考えるとします。
また、各点での接線ベクトル\(d\overrightarrow{l}\)を考えます。
接線ベクトルの大きさは、曲線上の微小な弧状の区間の長さであるとします。
(※各点での接線ベクトル自体は互いに逆向きの2方向がありますが、
PからQに向かう方向を考えます。)
経路における孤状の各区間についてベクトル場と接線ベクトルとの内積を考え、その総和を考えます。経路の分割を増やしていった時の極限値が接線線積分です。
曲線上の各点でのベクトル場と接線ベクトルの内積とその合計を考え、
経路の分割を増やした極限値を曲線に沿った点PからQまでの
ベクトル場\(\overrightarrow{F}\)の接線線積分と呼びます。
$$曲線上のPからQまでの接線線積分$$
$$\int_{PQ}\overrightarrow{F}\cdot d\overrightarrow{l}$$
あるいは、PやQは点(位置としてのベクトルと考えても同じ)という事をことわったうえで、通常の積分のように積分記号の上下に積分範囲の端点を分けて記す場合もあります。
また、曲線の範囲を指定して名前をつけて(例えばL)、
それを積分経路の範囲として記す事もあります。
$$P,Qを点として\int_P^Q\overrightarrow{F}\cdot d\overrightarrow{l}と書く場合もあります。$$
$$端点をベクトルとした場合:\int_{\overrightarrow{P}}^\overrightarrow{Q}\overrightarrow{F}\cdot d\overrightarrow{l}$$
$$L を曲線上の特定の部分として\int_L\overrightarrow{F}\cdot d\overrightarrow{l}と書く場合もあります。$$
接線ベクトルに使う文字自体は何でもよく、
l(エル)ではなくr,s,t等を使う事もあります。
また、接線単位ベクトル(大きさが1の接線ベクトル。\(\overrightarrow{l}\)とします。)と
微小な弧長(\(ds\)とします)を分けて、次のように書く事もあります。
$$接線線積分の別表記:\int_{PQ}\overrightarrow{F}\cdot \overrightarrow{l}ds$$
ここで、各微小区間の弧において考えている内積は通常のベクトルに対して考えるものと同じであり、それぞれのベクトルの大きさと、なす角の余弦との積を考えます。
尚、曲線上の各点を結んだ折れ線が、点の数を無限に増やした時に極限値を持つ事は三角不等式を使って確かめる事ができます。基本的には円周率の値を極限値として図形的に計算するやり方と考え方は同じです。
通常はそのままの形では接線線積分の具体的な値は計算できない事が多いので、余弦の値が確定するようなモデルを考えるか、積分を変形して計算できる形にして考える場合があります。
開曲線に対する接線線積分の基本となる考え方をまとめると次のようになります。
- 積分経路となる曲線の端点を決める(例えば点Pと点Q)
- 積分の方向を決める(例えばP→Q,あるいはQ→P)
- 曲線上の接線ベクトルは、積分の方向を向くと約束する
【曲線上のある点での接線は、
ある1つの方向とその逆向きの2方向があり得る → 片方に定める。】 - 曲線を、微小な区間で構成される折れ線であると考える
- 各区間で、ベクトル場と「微小区間の長さを大きさとする接線ベクトル」との内積を考え、積分経路全体での合計を接線線積分と定義
後述しますように、接線線積分の内積の部分を座標成分によって計算して、全体としてはスカラー関数の線積分として計算を進める方法もあります。
閉曲線に対する接線線積分
曲線が閉曲線(例えば円や楕円など)の場合にも、基本的な積分の方法は開曲線の場合と同じです。
ただし、積分方向に関する約束が開曲線の場合と異なるのです。
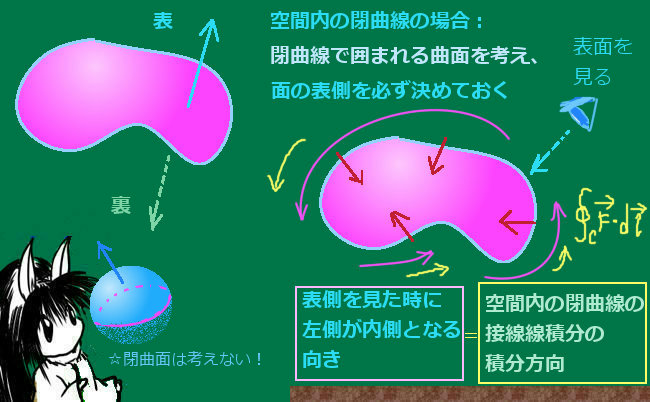
問題となるのは閉曲線に対して1周回転する形で接線線積分を行う場合であり、2通り存在する向きを1通りに確定させるための定義の仕方が存在します。
閉曲線全体が積分区間の場合には、ある点Pから積分を始めて同じ点Pに戻ってくる時に向きが2通りあり得ます。そのため閉曲線上の接線線積分を考える時には、積分の方向を約束して1通りに確定させておく必要があるわけです。
☆なお、閉曲線上であっても積分区間が閉曲線全体ではなく部分的な弧である場合には積分区間を開曲線とみなせばよいので、向きに関する約束は必要なく2点PとQに対してP→QなのかQ→Pなのかを決めておけば良い事になります。
周回積分と組み合わせた表記法
積分区間となる曲線が閉曲線(長方形や多角形も含みます)の全経路である場合、周回積分の記号と組み合わせて次のように接線線積分を書く表記法があります。
閉曲線をCとして、1周まわる形でC全体を経路として接線線積分を行う場合は、
次の表記をする事があります。
$$\oint_{C}\overrightarrow{F}\cdot d\overrightarrow{l}あるいは\oint_{C}\overrightarrow{F}\cdot \overrightarrow{l}ds$$
閉曲線上を積分する向きは、次のように約束します。
- 平面上の場合:接線線積分の向きは、反時計回りと約束。
- 空間内の場合:接線線積分の向きは、
「閉曲線で構成される面の法線ベクトルのプラス方向側(どちらがその方向か決めておく)から閉曲線を見た時に、『閉曲線の内側が左に来る向き』」と約束。
閉曲線を表す記号としてCを使う事が多いですが、これは英名 closed curve 等の頭文字を意味する事が多いと思われます。
周回積分である事を表す記号は省略される事もありますが、その場合でも閉曲線全体の接線線積分を考えているのであれば、積分の方向に関する約束は同様に適用されます。
接線積分の方向の約束①:平面上の閉曲線の場合
平面上だけで周回積分として接線線積分を考える時には、
積分する向きは反時計回りとして約束します。
この場合の「平面上」とは、
例えば、数学上のxy平面を考えて、そこでの閉曲線を考える場合などです。
$$周回積分の記号を省略して\int_{C}\overrightarrow{F}\cdot d\overrightarrow{l}と書いても向きに関する約束は同じ$$

平面上で閉曲線を考える場合のこの考え方は、図形が描かれている画面を見ている構図で考えると、空間内の場合での約束の仕方を理解する時に便利です。
接線積分の方向の約束②:空間内の閉曲線の場合
空間内での閉曲線を考える場合、閉曲線で構成される面の表側から見るか裏側から見るかによって、時計回りか反時計回りなのかが逆になってしまいます。
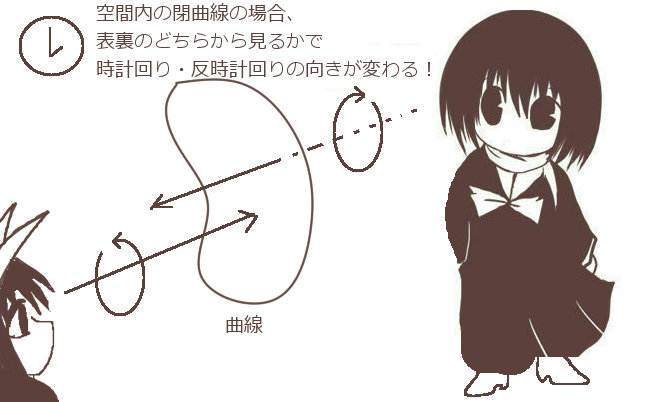
そのため、その場合にはまず、閉曲線で構成される面の「表側」(法線面積分において法線ベクトルがプラスになる側の面)を決めておきます。
そして、
「曲面の表側から曲面を見て、曲線上をたどった時に『閉曲線の内側が左側になる』向き」
を、接線線積分の積分方向であると約束します。
その方向を閉曲線Cの「正方向」とも言います。
この考え方のもとで、平面だけで考える場合の閉曲線上の積分方向は、
「図が描かれた画面を面の表側であると考えた場合」であると言う事もできます。

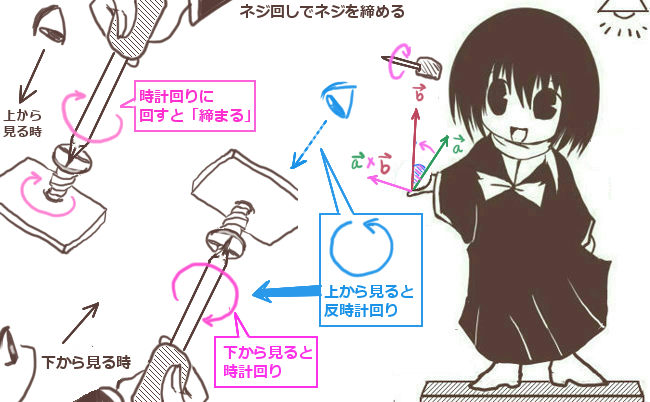
「右ねじ」の考え方
上記の、閉曲線に対する接線線積分の積分方向の約束は、より直感的な理解の方法もあります。
それは工具の「ねじまわし(ドライバー)」を使った考え方です。
まず、曲面の表面から出るベクトル(例えば法線ベクトル)の矢印の先を「一般的なねじまわしの先端」と考えます。そして、「『ねじを締める方向』が接線線積分の積分する向き」であると捉えると、これは前述の定義の仕方と一致するのです。

ねじ回しを上に向けて締める場合に上から見ると反時計回りで、
逆にねじ回しを下に向けて締める場合に上から見ると時計回りであり、
空間内の任意の閉曲線に対してこの考え方は適用できます。
これは一種の例えによる表現ですが、物理学で多く使われます。「右ねじの方向」「右ねじをまわす方向」など、いくつか呼び方があります。
その事を、回転の向きを表すものとして比ゆ的ですが数学や物理学でも使用する場合があります。
接線線積分の座標成分による内積計算
【スカラー場に対する線積分との関係】
さて、接線線積分の表記の中における内積で表されている部分については座標成分によって表す事もできます。これは、法線面積分における考え方と似ています。
この時に、ベクトル場の個々の座標成分はスカラー関数ですから、そのように表記した時には接線線積分は、「x,y,zを変数とするスカラー関数に対する線積分」に変化します。
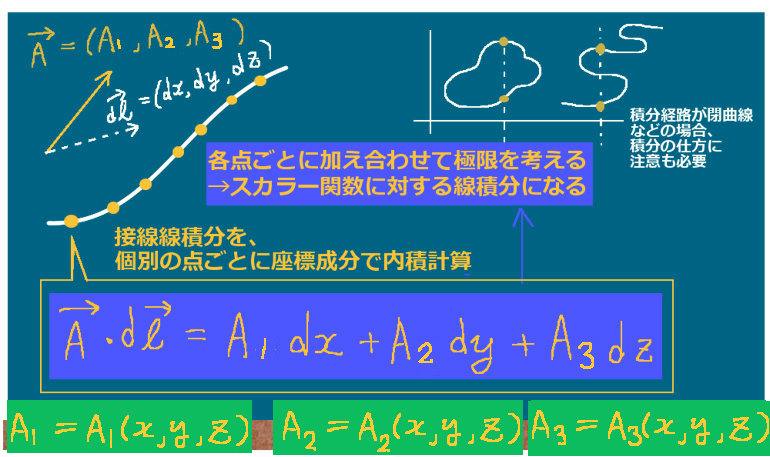
まず、接線ベクトルを座標成分で次のように書きます。
$$d\overrightarrow{l}=(dx,dy,dz)$$
そこで、ベクトル場に対する内積の計算をすると次のようになります。
$$\large{A_1=A_1(x,y,z),\hspace{5pt}A_2=A_2(x,y,z),\hspace{5pt}A_3=A_3(x,y,z)\hspace{5pt}}のもとで$$
$$\overrightarrow{A}=\large{(A_1,A_2,A_3)}\hspace{5pt}である時、$$
$$\large{\overrightarrow{A}\cdot\overrightarrow{dl}=A_1dx+A_2dy+A_3dz}$$
さてしかし、じつはこのように表記した時には積分をする時に、
どういった積分変数で積分を行うのかといった問題が起こる事があります。
この段階ではベクトル場の成分はx,y,zに関する多変数関数であるという前提があります。
そのため、それらをそのままの形で、例えばx単独で積分してしまうと問題が発生するのです。
また、この内積の計算は、曲線上の各点における接線ベクトルごとに行っています。
従って、積分変数を単独のx,y,zとしようとする時に、もともとの積分経路が閉曲線である場合や、開曲線であっても例えば曲がりくねって1つのx座標に対して対応するy座標が2つ以上ある場合には、全体の積分経路を個々の積分変数ごとに1つの積分区間で表せないという問題もあります。
x,y,zに関する多変数のスカラー関数として考えています。
従って、これらをx,y,zで積分しようとする時には注意が必要になります。
そこで、次のように考えます。
曲線という積分経路が指定されている場合には適切に経路を区切る事によって、その区切られた経路の範囲においては1つの変数の値を定めると1つの曲線上の点が定まる事を利用します。
その区切られた経路ごとにA1,A2,A3のそれぞれを、
xのみ、yのみ、zのみの関数として表します。
$$適切に区切った経路ごとに次の形で表現:\large{A_1=A_x(x),\hspace{5pt}A_2=A_y(y),\hspace{5pt}A_3=A_z(z)\hspace{5pt}}$$
※特に空間においての場合は、曲線上の特定の経路間という条件のもとで、スカラー場の関数を1変数のみで表す事ができます。
これによって、経路の区切り方に注意したうえで接線線積分をx,y,zそれぞれの1変数関数の積分の合計として表す事が可能になります。もちろん、具体的な値を1変数の定積分の合計値として計算するには、具体的な関数の形が明らかである事が必要です。
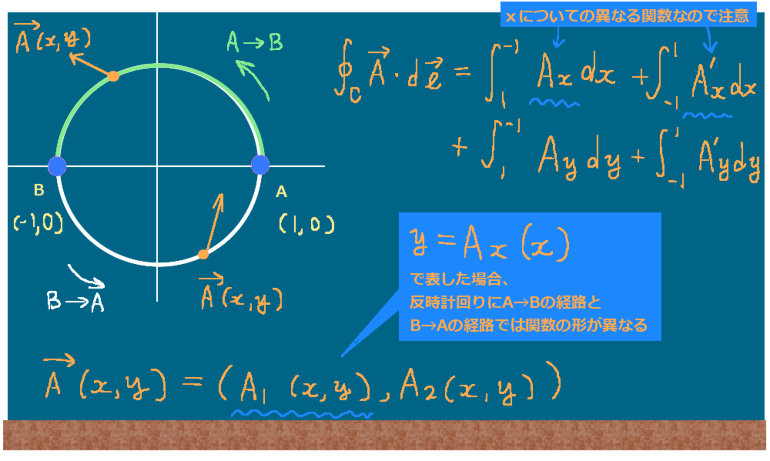
例として、平面上で接線線積分の積分経路が原点を中心とした半径1の円である場合に、内積を計算してから積分する事を考えてみましょう。
ベクトル場のx成分を「xのみの変数で表した関数」として考えて積分を行っています。
この場合、y成分について同様の事を考える場合には、別の区切り方が必要になります。
この時に、x方向の通常の定積分をしようとすると [-1,1] という1つの積分区間だけでは、元々の全体の積分経路である円周の半分についてしか内積のx成分についての項の合計を表せません。
そこで、xに関する定積分を2つに分けます。
まず点(1,0)から始めて(※)、
「x=1からx=-1に向かう」積分区間について、xを積分変数とする定積分をします。
この区間は、ここで考えている円の上半分に該当します。
※どこの点から積分を行っても、最終的に積分経路の全体に渡って積分を行っているなら同じ結果を得ます。
$$式で書くと\large{\int_1^{-1}A_xdx}を計算します。$$
そして次に、今度は(-1,0)から始めて(1,0)に戻る積分区間 [-1,1] の積分をします。この区間は、ここで考えている円の下半分に該当します。
同じ経路をたどって戻るのではなく、別の経路をたどって戻っています。
$$式で書くと\large{\int_{-1}^1A^{\prime}_xdx}を計算します。$$
ここで、元々の接線線積分の積分対象となっているベクトル場は円の上半分と下半分の経路上で一般的には異なるベクトルになっていますから、
その座標成分も一般的に異なるスカラー関数で構成されているわけです。
そのために、上記の積分の中ではAx とA’ xという形で、異なるスカラー関数である事を強調して書いています。(ここでは後者は微分という意味ではありません。)
xに関して「1→+1」の積分区間と「-1→+1」の積分区間の積分は、xに関して陽に表される関数(y=f(x)の形で表される関数。陽関数とも言います)としては異なるものに対する積分です。
ここでの例では具体的には、
\(\large{A_x}=\sqrt{1-x^2}\)
\(\large{A^{\prime}_x}=-\sqrt{1-x^2}\) として表せます。
y成分についても同じように考えます。
このように、接線線積分を内積計算によって「スカラー場に対する線積分」の計算にする時には、場合によっては積分する範囲等について注意が必要となります。ただしその事は、スカラー場に対する線積分の定義に組み込まれているものになります。
積分する範囲ごとの関数の形の混同を避けるために、スカラー場に対する線積分においても、接線線積分における積分経路をPQのように端点で表す表記方法もあります。
例えば上記の例の円において、(1,0)を点Aとして、(-1,0)を点Bとしたときに、ベクトル場の成分であるスカラー関数は共通のAxおよびAyで表して、線積分を次のように書く事もできます。
$$\large{\oint_{C}\overrightarrow{F}\cdot d\overrightarrow{l}=\int_{AB}A_xdx+\int_{BA}A_xdx+\int_{AB}A_ydy+\int_{BA}A_ydy}$$
この場合には、平面上の閉曲線(ここでは円)を反時計回りに回る約束で積分をする時に
A→BとB→Aの経路は異なる曲線(異なる2つの開曲線)と考えられるので、
「同一の1変数関数を同じ積分区間で行って戻って積分して合計は0 ??」・・・といった事には、一般的にはならない事を表現できるわけです。
接線線積分に関する定理とその応用
応用例として、ベクトル場に対する接線線積分は物理学の力学や電磁気学で使われます。特に、数学上成立する定理で応用でも重要なものとして、ストークスの定理と呼ばれる関係式が存在します。
応用例①:積分経路が開曲線の場合…仕事と位置エネルギー
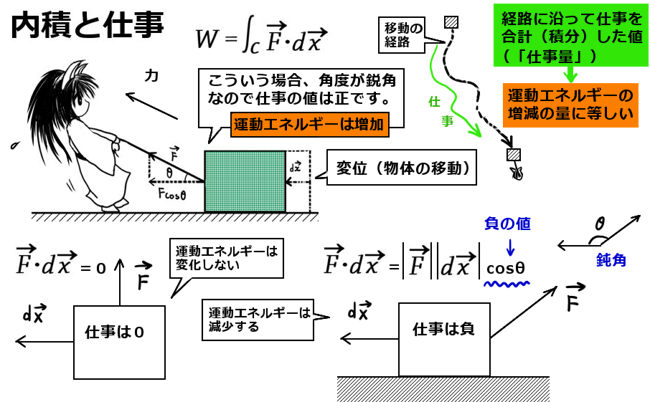
力学における「仕事量」は、接線線積分として定義されます。積分の対象となる関数は力ベクトルです。接線線積分による定義と計算から、別途に運動エネルギー、力学的エネルギーなどの概念が理論的に定義されます。
$$力\overrightarrow{F}によるPからQまでの「仕事量」:W=\int_{PQ}\overrightarrow{F}\cdot d\overrightarrow{l}$$
(「仕事」\(\overrightarrow{F}\cdot d\overrightarrow{l}\) の合計が「仕事量」)
◆補足:Fという記号は、数学では function(関数) の頭文字という意味合いで使う事が多いですが、力学では force(力)の頭文字という意味合いにする事が多いです。
この場合の積分経路は基本的には任意ですが、特に必要がなければ開曲線として考える場合が多いのです。これは、単純に「位置Pから位置Qまで物体が移動したとき」といった場合をモデルとして考えるためです。
力のうち、保存力がなす事が可能な「仕事」は、特に位置エネルギー(ポテンシャルエネルギー)とも呼ばれます。これも「仕事」ですから、数式的には接線線積分を考えるわけです。
静電場(時間変動の無い電場)による位置エネルギーは特に電位とも呼ばれ、これは「仕事」ですから力学におけるものと同じく接線線積分で表されるのです。ただし、位置エネルギーの積分範囲は基本的には「『無限遠』からある点まで」とする事が多いです。
$$静電場\overrightarrow{E}による点Pにおける「電位」:V_P=-\int_{\infty}^P\overrightarrow{E}\cdot d\overrightarrow{l}$$
それに対して、無限遠でない特定の2点間PとQの電位の差(QからPまで単位電荷を運ぶのに必要な電場の仕事量)を電位差あるいは電圧と言い、こちらは2点間の接線線積分として書かれます。
$$静電場\overrightarrow{E}による点Pと点Q間の「電圧」:V_{PQ}=\int_P^Q\overrightarrow{E}\cdot d\overrightarrow{l}\left(=-\int_Q^P\overrightarrow{E}\cdot d\overrightarrow{l}\right)$$
この「電圧」という語は、電線や電池、発電機等に対して使われる「電圧」と同じものです。
ただし、接線線積分で表される電圧の式は「電場をもとに計算する場合の式」ですから、別の要素によって電圧を決定できるか、あるいはそのように決定できるように状況を整えた場合には積分計算は不要になります。後述で簡単に触れている電磁誘導の法則はその例です。
応用例②:積分経路が閉曲線の場合…電磁気学、流体力学におけるストークスの定理
閉曲線に対する接線線積分に関する数学上の定理で、物理学・工学への応用上も重要なものとしてはストークスの定理があり、流体力学や電磁気学の理論計算で使われます。
ストークスの定理は、閉曲線に対する接線線積分と法線面積分を結びつける事ができる定理として知られています。ベクトル場の「回転」(記号では rot あるいは curl)を使用し、その回転という名称をつけている由来にも関係します。
閉曲線をCとし、Cで囲まれるS(閉曲面では無い)に対して次の関係が必ず成立します。
$$\oint_C \overrightarrow{F}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{F}\cdot d\overrightarrow{s}$$
左辺は接線線積分、右辺は法線面積分です。
※空間内の任意の閉曲線Cに対して、
「それぞれのCに対して定まる任意の『閉曲面では無い』曲面S」についてこの式が成立する
という事です。
つまり、閉曲線自身と閉曲線で囲まれる面を考えると、数学上定義される「ベクトル場の『回転』」の法線面積分の値は、面の縁に相当する閉曲線を文字通り「回転」するように接線線積分した値に必ず等しくなる、という事です。
ストークスの定理は、例えばアンペールの法則の積分形(「アンペールの周回積分の法則」とも。電流によって発生する環状の磁場を記述)を微分形に変換できる数学的な根拠となります。
逆に、アンペールの法則の微分形を積分形に変換できる事もストークスの定理により証明できます。
また、同様に電磁誘導の法則の微分形と積分形の変換もストークスの定理によって証明できます。電磁誘導の法則の積分形は、前述の「電圧」を発生させる状況を記述するものになります(※)。
(※)補足:電磁誘導の法則の積分形は電場の仕事量を接線線積分で計算するという形をとりますが、それは「磁場の時間変化によって決定できる」というのが法則の内容です。
従って、工学等で応用する場合には磁場の変化から計算するほうが簡単で電場から計算する必要は無い場合もあるわけです。
ストークスの定理は、もちろん自明に成立しているとは言えません。その証明方法はガウスの発散定理の証明に似ていて、関数をその偏微分の定積分とみなす事で証明を行います。定理の内容はベクトルの成分に関する3式の組み合わせになりますが、それら3式のそれぞれについて個別でも成立するという点でも似ています。