ヤングによる実験をもとにしている二重スリットを使った光の干渉実験は光の波動性を確認できるとともに、可視光の波長の概算的な測定ができる実験です。
また、光の干渉を利用した種々の干渉計のもとになっているという意味での重要性も持ちます。
数式的には三角比も含めた平面幾何的な考察によって、光の異なる2つの経路の長さの差(光路差)を計算する事により波長を含んだ関係式を導出できます。
この実験では光のコヒーレンス(可干渉性)の考え方も、重要な要素の1つとなっています。
模式図としては、分かりやすさのためにスリットの並びとスクリーン上の干渉縞が画面や紙面に対して縦方向に現れるように書かれる事が多くこの記事でもそうしていますが、実際の実験ではその方向が地面に対して平行であるようにする事がどちらかというと多いと思われます。
この記事では古典論での光の波動性を示す干渉実験について説明しています。
量子力学的な意味での二重スリット干渉実験もありますが、そちらでは粒子(とみなせる塊)を1つずつ、ある程度の時間の間隔をあけて二重スリットに向けて打ち出すという手法がとられます。ただしスリットのどちらかを狙い打ちするように打ち出すのではなく、スリットを通過する際に「どちらのスリットを通過したか不確定である」ようにします。そこがヤングによる干渉実験と異なる部分となります。量子力学的な二重スリット干渉実験は20世紀後半以降、電子や光子、一部の分子(比較的分子量が大きいものも含む)などについて行われています。
人の目に見える領域の光である「可視光線」の波長は実は非常に短く、
「ナノメートル」や「マイクロメートル」の単位のスケールでの長さとなります。
単位についてのメートルとの関係は次の通りです。
【nm】・・・「ナノメートル」 1【nm】=10-9【m】
【μm】・・・「マイクロメートル」 1【μm】=10-6【m】
【mm】・・・「ミリメートル」 1【μm】=10-3【m】
「センチメートル」【cm】は10-2【m】(百分の1メートル)になります。
■関連サイト内記事:
スリットとは【実験の概要】
スリット(slit)は物理の実験用に使われる板などに開けた非常に細い隙間の穴の事であり、
二重スリットあるいはダブルスリット(double slit, double-slit )は非常に近い間隔でスリットが2つある構造を指します。
slit とは英語において通常の語としても使われており、
「(刃物等による)切れ目」とか「切れ目を入れる」という意味で使われます。
「スリット」という言葉は実は現代日本語でも使われる時があり、パンや服、その他の色々なものに施された切れ目や溝、細い穴を指してスリットと言う事があります。
光の干渉(「かんしょう」)を調べる実験では、二重スリットにおけるそれぞれのスリットから光を出してスクリーン上に当てて波が強め合う位置(明るくなる)と弱め合う位置(光がなく暗く見える)が現れる事を見ます。それが縞模様のように見える事が多いので明暗のパターンの模様を干渉縞(「かんしょうじま」)と呼ぶ事もあります。
また、ある位置で2つ以上の光の重ね合わせの事を干渉光と呼ぶ事があります。
干渉は波動一般に対して起こる現象です。
ある位置で2つ以上の波の波形がぴったりと重なっていると合計として1つの大きな振幅の波となって強め合い、逆に波の最大値(プラスの値)と最小値(マイナスの値)が重なってしまうと波がつぶれて振幅が任意の時刻で0になってしまい弱め合います。
ここでは2つの光線の干渉を考えますが、3つ以上の光線の干渉を考える事もできます。
光には結論から言うと波動性がありますが、もし波動性が無くて「粒子(の集まり)としてだけ」振る舞うとしたらそのような縞模様ができる必然性がないので、干渉縞が現れる事が波動性を持つ事の根拠であるとして物理学的には解釈されているわけです。
実験用に使う二重スリットには色々なものがあり得ますが例としては、
1つのスリット自体の幅は0.1【mm】程度(光が回折するのに必要なおおよその細さ)、
2つのスリット間の距離は0.1~1.0【mm】程度のものがあります。
(スリットが開けられているスリット板の大きさは、例えば横10cm,縦5cm程度など。)

基本的に、光の干渉を調べる時にも同じ状況を作る必要があります。
スリットから出た波が広い範囲に広がっていくようにするには波の回折の現象を利用します。
可視光線の干渉の場合、波が強め合う位置は明るい点や線となって見えて、波が弱め合う位置は明るさが無く暗く見えます。
1つ1つのスリットからは1方向だけに光線が出るのではなく、非常に広い範囲にたくさんの光線が広がって行く形になります。これは波の回折現象を利用しており、波動性がなければ干渉同様に発生しない現象でもあります。
そのためにスクリーン上の各点では2つのスリットから出た光線のあらゆる重ね合わせが連続的に映し出される事になり、その中で特に光が同位相で強め合う部分と、半波長だけずれて弱め合う部分が目立って見えて干渉縞が形成されるわけです。
光は非常に細いスリットを通過する事ができます。
ただし、二重スリットの実験においてはスリットは意図的に細いものを使います。それはスリットにおいて波の回折を起こさせるためです。
回折とは波が小さい隙間に入り込み、そこから出る時に同心円か同心球状に大きく広がっていく現象です。イメージとしては水面に何か物が落ちた時に波紋が広がっていくような事が波が隙間から出る時に起きる事を指します。しかし回折はどんな波に対してどのような隙間に対しても起こるわけではなくて、基本的には波の波長が短いほど短い隙間が必要になります。
そして結論から言うと可視光線(色として人に見える領域の光)の波長はおおよそ
400【nm】~700【nm】の範囲であり、標準的な音波と比較しても非常に短い波長です。
光の干渉に使うスリットに「細さ」が求められるのはそのためであり、基本的に可視光線のて回折を起こさせるためには0.1ミリメートル程度かそれ以下の細さのスリットを使う必要があると言われます。
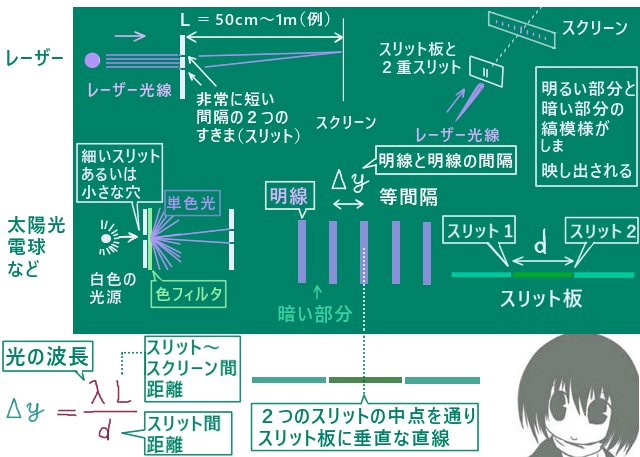
光源としては広がりが十分狭い「点光源」とみなせるものを使う必要があります。
単色光に近い光の干渉縞の明線の間隔はほぼ一定値です。
ただし、スクリーンの原点部分から離れるにつれて光の強度は小さくなっていくので明線の明るさも少しずつ減っていきます。
波動が正弦波であるとすると、干渉の効果を式で表す事もできます。
2つの光路の大きさをそれぞれR1とR2とすると2つの波はそれぞれ y=Asin(kR1-ωt),y=Asin(kR2-ωt)で表され、それらの波の重ね合わせは三角関数の和積の公式または加法定理により次式で計算できます$$A\sin(kR_1-\omega t)+A\sin(kR_2-\omega t)$$
$$=2A\sin\left\{\frac{k(R_1+R_2)}{2}-\omega t\right\}\cos\frac{k(R_1-R_2)}{2}$$この式で余弦の部分は時間に依存しないのでR1とR2の値によって決まる「振幅」の一部だと見なせます。余弦の部分は時間に依存せず、光路差(の絶対値)| R1-R2|にのみ依存して干渉光が強め合ったり弱め合ったりする事を表します。

光の波長と干渉縞に対して成立する関係式
スリット板の中央から垂直に線を引いて、
その線とスクリーンとの交点をここでは「スクリーン上の原点」と呼んでおきます。
スクリーンとスリット板は平行になるようにきちんと立てます。(片方だけ傾いていると結果がおかしくなります。)
光の干渉に関する二重スリットの実験の結果に使う数値は次の通りです。波長を除くと、使用する記号は他のものが使われる事もあります。
- λ【m】光の波長(可視光ではおおよそ400【nm】~700【nm】の範囲)
- L【m】スリット板中央からスクリーン原点までの距離(数十【cm】~3【m】の範囲等)
- d【m】スリット板における2つのスリット間の距離(0.1~1.0【mm】程度)
- y【m】スクリーン上における、原点部分からの距離。(スリット板に平行な方向。)
(座標のようにプラスマイナスの値で考える事もあります。) - Δy【m】スクリーン上に現れる明線間の距離(数ミリメートル~数センチメートル程度)
その他に、整数nや奇数2n+1などを式中で使います。具体的な数値は色々な場合があり得ますが、光の波長の範囲を考えると特定の数値を極端に大きくしたり小さくし過ぎたりすると上手く測定ができない事につながります。
以下に示す関係式を使う時にはスリットとスクリーン間の距離Lは、yやdと比べて十分大きい値になっている必要がありますが、それについても、極端にLが大きすぎてもおかしくなります。
スリット間の距離については「d」の文字が使われる事が多いのでここでもそうしていますが、微分や微小量とは直接的に関係はありません。ただしそれなりに短い間隔ではあります。
光源としてはレーザー光線のように単色とみなせて位相が揃っている(コヒーレントである)ものを使うのが望ましく、
白色光を使う場合は小さい穴に通して点光源化し、色フィルタ等を置いて多くの波長の光を除外して単色に近くなるようにします。そこから回折により同じ位相の揃った単色に近い波が広がって進行し、二重スリットに至るようにします。
二重スリットによる光の干渉実験において、
上記の量と光の波長の関係式は次のように表されます。
■波長をL,d,Δyで表す式
$$\lambda = \frac{(\Delta y)d}{L}【波長を表す式】$$
$$\Leftrightarrow \Delta y=\frac{\lambda L}{d}【明線の間隔を表す式】$$
■光路差が波長の整数倍になる事および明線の位置を表す式
(nは整数。n=0の時はスクリーン中央、n=1の時はΔyを使った式と同じです。)
$$n\lambda=\frac{yd}{L}$$
$$\Leftrightarrow y=\frac{n\lambda L}{d}$$
■y/L=tanθ を使った場合の表記
(θが小さい値の時に成立。)
$$n\lambda=d\tan\theta≒d\sin\theta≒d\theta$$
波が弱め合う条件を考える場合にはmを「奇数」としてmλ/2を考えて
yd/L≒mλ/2とするか、
あるいは「波長の整数倍に半波長が加わっている」と考えて
yd/L≒(n+1/2)λのようにします。
奇数mをm=2n+1と書けば
mλ/2=(n+1/2)λとなるので、上記2式は同じものです。
可視光の波長のおおよその範囲が
400【nm】~700【nm】=4×10-7【m】~4×10-7【m】なので、
上記の関係式Δy=λL/dから判断すると
Lやdの値によってはΔyの値が小さくなり過ぎて
「干渉縞がつぶれてしまって測定できない」という事もあり得る事が分かります。
仮にd=0.10【mm】=1.0×10-4【m】でL=1.0【m】であるとします。
この時にλ=500【nm】=5.0×10-7【m】の光を光源に使うとすると
Δy=λL/d=5.0×10-3【m】=5.0【mm】となり、
おそらく目視で干渉縞を確認できるだろうという計算になります。
(n=1~4くらいまではL がyに対して十分大きいという前提条件も確認できます。)
可視光の波長はいわゆる「色」(普通の赤、青、紫などの色)で特徴づけられます。白色に関しては色々な波長の光が混ざったものです。
(黄寄りの赤・紫寄りの青・緑の光を混ぜると大体白色になるとされます。)
また「物体の色」に関しては白色光等から特定の波長の光が吸収されて、
残りが反射される事で「補色」が見えているというのが一般的に言われる事です。
| 波 | おおよその波長 特に光では幅がある | 備考 |
| 紫色の光 | 約400 ~450【nm】付近 | 約380【nm】を下回ると紫外光 (基本的に人の目では見えない) |
| 青色~ 水色の光 | 約450 ~500【nm】付近 | 紫色・緑色との境界は曖昧 |
| 緑色の光 | 約500 ~550【nm】付近 | 水色・黄色との境界は曖昧 |
| 黄色~ 橙色の光 | 約550 ~600【nm】付近 | 緑色・赤色との境界は曖昧 |
| 赤色の光 | 約600 ~700【nm】付近 | 約780【nm】を超えると赤外光 (基本的に人の目では見えない) |
| 音波 | 約1.715【m】 | 空気中,20【℃】200【Hz】で 音速約343【m/s】の場合 |
ただし光でも目に見えない領域では種類によっては波長が長く、
例えばラジオ波と呼ばれる領域だと波長が1【m】を超える事もあります。
逆に紫外線やX線の領域だと波長は可視光よりもさらに短くなります。
可視光のそれぞれの「色」にも幅があるわけで、例えば「紫色」は大体400【nm】付近の色と言う事はできても「ぴたりと397ナノメートルの色」のようにはなかなか言えません。しかし物理的には同じ紫色でも具体的な測定対象の光に対して「どのような紫色なのか」を波長によって定量的に表す事ができて(それに意味があるのか、活用の仕方は何かという事はまた別の議論として)、その測定方法の1つとして二重スリットによる干渉実験があるわけです。
関係式の導出(図形的考察)
スクリーン上の原点からy【m】の位置に向かう2つのスリットからの光線に着目して、
「1つの光線に対するスリットからスクリーン上の点までの距離(光路の長さ)」の差
である光路差を図から計算する事を考えます。
この計算はいくつかやり方があって、ここではそのうちの2つを説明します。
図の見た目は一見単純なのですが意外と結構くせもので、
「スリット板~スクリーン間の距離Lがyやスリット間距離dに対して十分大きい」という条件から近似(角度や平行関係含む)を行わないと関係式の導出がうまくできないので注意が必要です。
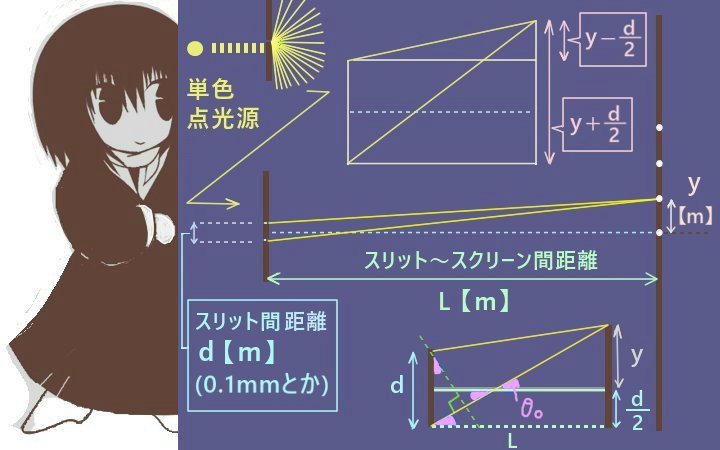
三角比を使う場合
三角比を使う場合は式の構造は単純ですが、図において厳密に成立する関係と近似によってほぼ成立すると見てよいものを区別する必要がある事に注意が必要です。
まず厳密に成立する関係を見るために図の下側のスリットからの光線に注目して、
「スクリーン上の原点とスリット板中央を結ぶ直線」とのなす角をθ0とします。
(あるいはスリット板に垂直な任意の直線とのなす角と考えても同じです。)
ここではθ0とθという2つの角度を考えて、それらが近似的にほぼ等しいとみなせるという形で関係式を導出しますが、最初から2つを同一視して話が進められる事も多いです。得られる結果は同じです。
次に図の下側のスリットからの光線に対して、上側のスリットから垂線を引きます。
その垂線とスリット板とのなす角はθ0に等しくなります。
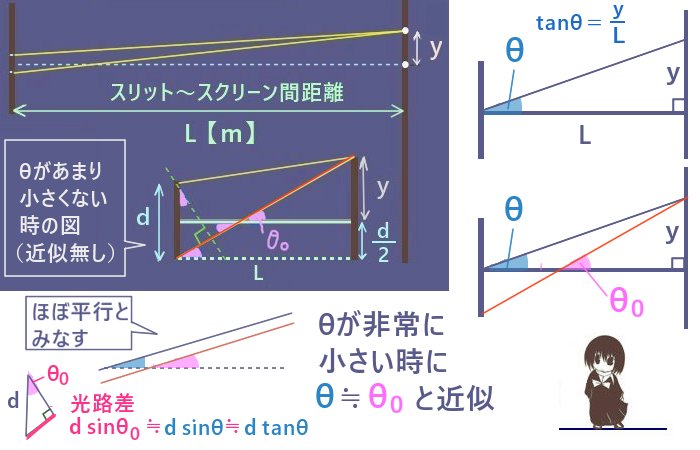
ここでLが十分大きいとして近似を行います。まず、2つの光線は平行ではありませんが
「ほぼ平行」と考えて光路差はdsinθ0であると考えます。
さらに2つの光線は平行とみなせるほどになす角が小さいとします。
すると、スリット板中央から「スクリーン上の原点よりyの距離の位置」に対して引いた直線も2つの光線とほぼ平行と見なせます。
今、θを tanθ=y/Lを満たす角度とすると、上記の近似によりθ0≒θとできるので、
光路差はdsinθ0≒dsinθと書く事ができます。θの値が小さい時にはさらにsinθ≒tanθの近似式も成立するのでdsinθ≒dtanθ=yd/Lの関係が近似的に成立します。
【cosθ≒0のもとでtanθ=(sinθ)/(cosθ)≒sinθ】
そこで、スクリーン上で波が強め合う条件としては光路差が「波長の整数倍」になっている事を考えればよいので、nを整数として次の関係式を導出できる事になります。
- dsinθ≒nλ
- dtanθ=yd/L≒nλ
- y≒nλL/dにより、Δy=λL/d
【Δy=(n+1)λL/d-nλL/d=λL/d】
【単純にn=1の時を考えてΔy=λL/dとしても同じです。】 - λ=Δyd/L
以上の方法は、近似を認めるなら非常にシンプルで分かりやすいとも言えますが、肝心の近似が本当に成立するのかが図だけからは分かりにくい(図では説明の都合上、拡大して描かれる事が多いので)という事も同時に言えるかもしれません。
上記の近似を本当にしてもよいのかという事に関する考察は平面幾何的に考える事も可能ですが、次に見て行く光路差の別の導出方法から計算される結果の一部を使って後述する事にします。
また、この時に sinθ≒θである事もよく強調されます。(θは弧度法での角度とします。)
これはマクローリン展開からsinθ=θ-θ3/(3!)+θ5/(5!)-・・・
と書けるので、θが0に近い値の時にはベキ乗の項は全て0に近似できるとするものです。
例えばθ=0.01であればθ3/(3!)=0.000000166・・・となるので、
θ=0.01に対して「ほぼ無視できる」
(測定の結果にほぼ無影響と考えてよい)とするわけです。
あるいは、θ=0における正弦関数の微分係数は1であるので、θが0に近ければ
近似1次式として1・θ=θがsinθに非常に近い値になると考える事もできます。
また余弦に関してはcosθ=1-θ2/(2!)+θ4/(4!)-・・・が成立します。
ここで先ほどと同じように例えばθ=0.01の時には
cosθ≒1-0.000025+・・・≒0999975なので、
tanθ=(sinθ)/(cosθ) の関係から
θが小さい時のtanθ≒sinθの近似式も成立しているとみてよい事が分かります。
一般二項定理で平方根を展開する方法
光路差を計算方法としては、平方根を展開して直接計算するというものもあります。
まず近似のない状況下で三平方の定理によって2つの光路の大きさを計算しておきます。それは平方根を使って書けるわけです。
次に少し式を変形してから、
(1+P)1/2の形の式に対する一般二項定理による展開を使って光路の大きさを表す式を変形します。(マクローリン展開と考えても同じです。)
近似を使うのはそこからで、yやdに対してLが十分大きいという条件から展開式の第3項以降は0に近い数値であるとみなす事で、式が簡単になります。
それから光路差を丁寧に直接計算(単純な引き算)すると、光路差がほぼyd/L(≒tanθ)に等しいという事を導出できます。波が強め合う条件から波長を含んだ関係式を作るのは三角比を使った導出の時と同じになります。
具体的な計算は次のようになります。
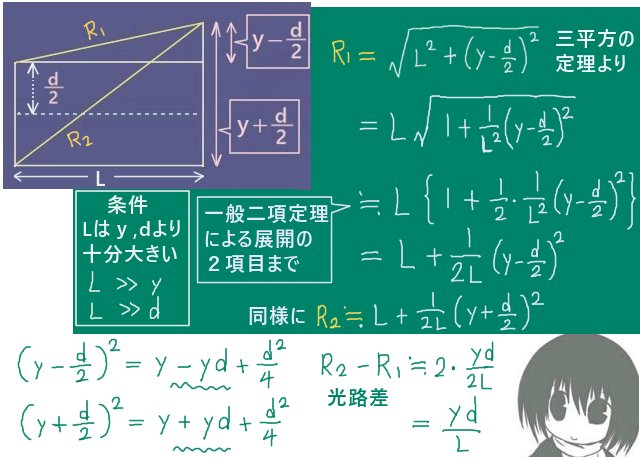
2式の違いは、y-d/2を考えるかy+d/2を考えるかの所だけです。
| 図の上側のスリットからの光路の長さ | \(\sqrt{L^2+\left(y-\frac{\Large d}{\Large 2}\right)^2}=L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y-\frac{\Large d}{\Large 2}\right)^2}\) |
| 図の下側のスリットからの光路の長さ | \(\sqrt{L^2+\left(y+\frac{\Large d}{\Large 2}\right)^2}=L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y+\frac{\Large d}{\Large 2}\right)^2}\) |
これらを一般二項定理で展開します。(1/L) (y-d/2)=y/L-d/(2L)が0に近い値である条件のもとで 3項目以降はほぼ0と考えて、2項目まで残したものに近似すると次のようになります。
| 図の上側のスリットからの光路の長さ | \(L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y-\frac{\Large d}{\Large 2}\right)^2}≒L+\frac{\Large 1}{\Large 2L} \left(y-\frac{\Large d}{\Large 2}\right)^2\) |
| 図の下側のスリットからの光路の長さ | \(L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y+\frac{\Large d}{\Large 2}\right)^2}≒L+\frac{\Large 1}{\Large 2L} \left(y+\frac{\Large d}{\Large 2}\right)^2\) |
光路差はマイナスの値になっても別に構わないのですが、分かりやすさのために下側の光路の長さから上側の光路の大きさを引く事で光路差を計算すると次のようになります。光路差が波長の整数倍であるとおけば光が強め合う位置での関係式が導出されます。
| 光路差 の近似式 | \(\left\{L+\frac{\Large 1}{\Large 2L} \left(y+\frac{\Large d}{\Large 2}\right)^2\right\}-\left\{L+\frac{\Large 1}{\Large 2L} \left(y-\frac{\Large d}{\Large 2}\right)^2\right\}\) \(=\frac{\Large 1}{\Large 2L}\left(2\cdot\frac{\Large yd}{\Large 2}\right)-\frac{\Large 1}{\Large 2L}\left(2\cdot\frac{\Large -yd}{\Large 2}\right)=\frac{\Large yd}{\Large L}\) |
| 波が強め合う 条件 | \(\frac{\Large yd}{\Large L}=n\lambda\), \(\frac{\Large \Delta y d}{\Large L}=\lambda\)【三角比を使って導出した時と同じ】 |
この導出方法だと、途中計算が少し複雑に思える部分もあるかもしれませんが、yやdに比べてLが十分大きい時にどの項を0に近似しているかが比較的明確になるとも言えます。
(x+y)aに対する二項展開は指数が任意の実数値でも自然数の時と同じ形の式として書く事ができて次式のようになります。(一般的には無限級数です。)
■一般の式
【厳密には、a が自然数でない時には式が収束する事が保証されるのは(1+P)a の形で|P|<1の時なので、一般の場合には式変形をしてその形にする事が必要。】
$$(p+q)^a=p^a+ap^{a-1}q+\frac{a(a-1)}{2!}p^{a-2}q^2+\frac{a(a-1)(a-2)}{3!}p^{a-3}q^3+\cdots$$
■上式で a =1/2とした場合は平方根の展開式の1つ
$$\sqrt{p+q}=(p+q)^\frac{\large 1}{\large 2}$$
$$=p^{\frac{\large 1}{\large 2}}+\frac{1}{ 2}p^{-\frac{\large 1}{\large 2}}q+\frac{\frac{\large 1}{\large 2}\cdot\left(-\frac{\large 1}{\large 2}\right)}{2!}p^{-\frac{\large 3}{\large 2}}q^2+\frac{\frac{\large 1}{\large 2}\cdot\left(-\frac{\large 1}{\large 2}\right)\cdot\left(-\frac{\large 3}{\large 2}\right)}{3!}p^{-\frac{\large 5}{\large 2}}q^3-\cdots$$
$$=p^{\frac{\large 1}{\large 2}}+\frac{1}{ 2}p^{-\frac{\large 1}{\large 2}}q-\frac{1}{8}p^{-\frac{\large 3}{\large 2}}q^2+\frac{1}{16}p^{\frac{\large 5}{\large 2}}q^3-\cdots$$
■特にp=1かつa =1/2の場合の式は次式です。
$$\sqrt{1+q}=(1+q)^\frac{\large 1}{\large 2}$$
$$=1+\frac{1}{ 2}q-\frac{1}{8}q^2+\frac{1}{16}q^3+\cdots$$
■さらに、qが0に近い値なら次式に近似できます。
$$\sqrt{1+q}=(1+q)^\frac{\large 1}{\large 2}≒1+\frac{1}{ 2}q$$
■さらにq=\(\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2\)とした時
\(\sqrt{
1+\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2}
=\left\{
1+\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2
\right\}^{\frac{\large 1}{\large 2}}
\)
\(=1
+\frac{\Large 1}{\Large 2L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2-
\frac{\Large 1}{\Large 8}\frac{\Large 1}{\Large L^4}\left(y\pm\frac{\Large d}{\Large 2}\right)^4
+\cdots【ここで3項目以降は0に近似可能】\)
\(≒1
+\frac{\Large 1}{\Large 2L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2\)
よって、\(L\sqrt{
1+\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2}
≒L+\frac{\Large 1}{\Large 2L}\left(y\pm\frac{\Large d}{\Large 2}\right)^2\)
上記では平方根を展開して第2項まで近似した状態で関係式を導出しましたが、
第2項もじゅうぶん0に近いとして近似すれば
斜辺の長さを底辺とほぼ同じ L として考える事もできます。
そこまで近似するとやり過ぎ感もあるかもしれませんが、実際のところは
それが「θが小さい値の時に tanθ≒sinθ」とする近似に他なりません。
【三角比の定義から考えてみてもb/a≒b/cつまり a≒cという近似です。】
上記の計算からは、考えている諸量(L,dなど)がどのような値の時にその近似をしてよいかがより具体的に分かるとも言えます。
斜辺を底辺とほぼ同じとみなす近似のもとで
前述の三角比による計算でのsinθ0を数式で書いてみると、$$\sin\theta_0 =\frac{y+\frac{\Large d}{\Large 2}}{L+\frac{\Large 1}{\Large 2L} \left(y+\frac{\Large d}{\Large 2}\right)^2}≒\frac{y+\frac{\Large d}{\Large 2}}{\large L}$$ところで sinθ≒tanθ=y/Lですから、sinθ0≒sinθ≒tanθ=y/Lの近似が成立するには
「yに対してd/2がじゅうぶん小さい時」
つまりy+d/2≒yと見なせる時であると言えます。
実の所それは図で見てもそうであるわけですが、数式的に考えるのであれば例えばこのような方法もあるという事になります。
例えばd=1.0×10-4【m】,L=1.0【m】,λ=5.0×10-7【m】であれば、
三角比を使わない方法でもΔy≒λL/dの関係式は導出できた事にも注意して
Δy≒λL/d=5.0×10-3【m】なので
「n=1の時のy」(=Δy) とd/2は100倍の大きさの違いという事になります。
これもまた図形的にも見る事ができますが、n=2,3の時には
yの値は2倍,3倍になるのでyとd/2の倍率の違いはさらに大きくなる事が分かります。
以上の計算は考察の方法の1つであり、考え方は他にもあります。
干渉光の強度の式
干渉縞の明線の間隔Δyは一定値となりますが、yが大きくなると光の重ね合わせの「強度」は小さくなっていきます。それに対応する形で、明線の明るさはスクリーン中央で最大であり、中央から離れていく(yおよびnが大きくなっていく)ほどわずかに薄く弱い輝きになっていきます。
光を正弦波で表せると仮定した時、光の強度定量的に表すと次のようになります。
正弦波の「強度」は定量的には「波の振幅の2乗」として定義されます。
【振幅の2乗に比例する量として考える事もありますがここではその比例係数を1とします。】
重ね合わさる前のもとの光の振幅がともに A【m】で、
強度もともに等しくA2=I0であるとすると
スクリーン上での2つの光の重ね合わせ(「干渉光」)の強度は次式で表されます。
$$I=4I_0\cos^2\left(\frac{\pi yd}{\lambda L}\right)$$
$$=4A^2\cos^2\left(\frac{\pi yd}{\lambda L}\right)$$yが増えて行くと余弦の値が小さくなり、強度も小さくなるという計算になります。
この式の余弦の中身は実験で使っている諸量に由来しますが、「余弦自体」は二重スリット実験における図形的な位置関係に由来するものではない事に少し注意が必要です。つまり、二重スリット干渉実験で波長を表す近似式で使っている三角比とは別物です。
強いて表すなら、近似式で使った三角比は強度を表す式の「余弦の中身」に入ります。
$$I=4I_0\cos^2\left(\frac{\pi yd}{\lambda L}\right)≒4I_0\cos^2\left(\frac{\pi d\sin\theta}{\lambda }\right)≒4I_0\cos^2\left(\frac{\pi d\tan\theta}{\lambda }\right)$$
光の波が正弦波であると仮定した時の干渉光の強度に関する式は、この記事内でも少し触れた加法定理による重ね合わせの式から導出できます。すなわち、正弦と余弦の積になった形の式において時間変動を含まない部分を余弦も含めて振幅とみなして2乗する事で上式が導出されます。整理してまとめると次のようになります。
| スクリーン上の1つの点で 正弦波で表された2つの光 | Asin(kR1-ωt) Asin(kR2-ωt) |
| 重ね合わせて加法定理 により得る干渉光の式 | \(2A\sin\left\{\frac{\Large k(R_1+R_2)}{\Large 2}-\omega t\right\}\cos\frac{\Large k(R_1-R_2)}{\Large 2}\) |
| 光路差を表す式 | \(R_1-R_2≒d\tan\theta=\frac{\Large y d}{\Large L}\) |
| 波数の定義 | \(k=\frac{\Large 2\pi}{\Large \lambda}\) |
| 干渉光の振幅 (時間変動を含まない部分) | \(2A\cos\frac{\Large k(R_1-R_2)}{\Large 2}=2A\cos\left(\frac{\Large \pi yd}{\Large \lambda L}\right)\) |
| 干渉光の強度 (振幅の2乗) | \(4A^2\cos^2\left(\frac{\Large \pi yd}{\Large \lambda L}\right)=4I_0\cos^2\left(\frac{\Large \pi yd}{\Large \lambda L}\right)\) |
波長λは波数の定義から式に入っている事になります。
同じように正弦波で表せる仮定のもと、波動を敢えて複素数で表す場合でも(指数関数表示・極形式による表示では三角関数を含む形になるので)同じ式を導出できます。
その場合には強度は複素数で表した波の絶対値の2乗として定義し、
波を重ね合わせた時の強度は形式的に余弦定理を使った形の式で表されます。
その式において2つの波の振幅は同じであるとして加法定理、半角の公式、倍角の公式のいずれかを適用する事で上記と同じ形の式が得られます。
光源に要求されるコヒーレンス(可干渉性)
ところで、光の二重スリット干渉実験では光源として使用する光の種類についての考察も重要な実験の要素の1つと言えます。
波の干渉を調べる場合、2つ以上の波が強め合うかつぶれて弱め合うかを解析して計算をするにはどこか最初の位置で「位相を同じ値にしておく」という制御が必要です。
その事は、二重スリットの部分においては波の回折を起こさせる事で実現しています。つまり元々位相がそろった波面の波を2つのスリットに進入させる事によって、その2点から進む「同時刻で同位相の2つの光」の光路の長さと波形のずれの関係を適切に計算できるわけです。
他方で、二重スリットに入る光のもとになっている光源の光の種類にも実は注意する必要があります。光の二重スリット干渉実験の光源としては結論としてはレーザー光を使うのが最も好ましいわけですが、逆にそれ以外の光ではだめなのかという話にもなります。
太陽光やいわゆる「白色光」には実は多くの波長の光が混ざっています。
そのため、そのような光をそのまま光源に使って直接的に二重スリットに通しても干渉縞が発生しないか、干渉縞が観測できても上手く測定ができないという事があるのです。
光の干渉実験に白色光を使う場合には
①光源からの光を小さい穴に通して回折を起こさせて位相を揃えた波を作る
②色フィルタ等をおいて単色光に近い光にする
という工夫が必要になります。
もし①だけ行って②を行わない場合、虹のようなたくさんの色の干渉縞が現れます。そのような干渉縞は、測定があまりしやすくない事があります。
光の二重スリット干渉実験にもとになっているのはイギリスの人ヤングによる実験(19世紀初め頃)で、当時は光源として太陽光を使って光の干渉を確かめる実験が行われたと言われます(当時はレーザー光は利用不可能)。その時に干渉縞はしっかりと確認されて、光の波動性が確認された最初の実験であるとされます。また、残っている講演の資料等によるとヤングは光の干渉を上手く起こすためのコヒーレンシーの考え方(用語自体ではなく)についても当時から指摘していたとされます。
それに対してレーザー光は単色とみなせるほどに波長の幅が小さい光であり、また位相もそろっている光です。レーザー光のように波動(主に光)の位相が揃っている事を指して可干渉性あるいはコヒーレンスと呼び、そのような性質を持った光をコヒーレント光あるいはコヒーレントな光であると分類する事があります。太陽光や白色光は一般的にコヒーレンスを備えていません。
レーザー光線は基本的に人工的に形成される光ですが、光の干渉を調べる時に使う光源としては最適です。重要な特徴を整理すると次のようになります。
- 単色性:非常に近い値の波長の光だけで構成され、ほぼ単色とみなせる。
- 可干渉性(コヒーレンス):位相がほぼそろっている光で構成されており、精度の高い干渉縞を観測可能。単に「干渉性」と言ったり、コヒーレンシーと呼ぶ場合もあります。
- 指向性(収束性):長距離を光があまり広がる事がなく進行し、非常に狭い範囲に光を集める(収束させる)事が可能。
- 高出力性および高輝度性:時間あたりに放出するエネルギーが非常に大きい光(材料加工などに使用)であり得る。光の干渉実験で使うレーザー光は、出力としては弱いものを使用します。
詳しく見ると、コヒーレンス(coherence)には波の位相の波数および位置座標を含む項に由来する「空間的なコヒーレンス」と、角周波数および時間を含む項に由来する「時間的なコヒーレンス」があります。レーザー光は空間的にも時間的にもコヒーレントな光ですが、それが特定の物質を通過して拡散する事で、時間的なコヒーレンスだけを備えた光になるという事もあり得ます。
coherent という語は少し聞き慣れない語かもしれませんが一応普通に使われる語でもあり、密着しているとか結合しているといった意味合いが元々あって、転じて「話や議論の筋が通っている、理路整然としている」 といった意味などとして使われます。
