物理の理論では、微分とは少し意味合いが異なる変分という計算が行われる事があります。
変分とは?例①:光の屈折
■ 汎関数という考え方 ■ 2点間を進むための最小時間と光の屈折 ■ 変分の記号と計算
汎関数という考え方
ある関数 y = F(x) があった時、それをグラフに描いたとして、グラフの「弧長」sを決定する事ができます。この弧長sは、もちろん関数によって異なります。2端点が決まっている場合、 y = F(x) が どのような関数であるかに依存してsが決まるわけで、s=s(y) という関数であると考える事もできるわけです。このようなタイプの関数を汎関数と言います。
関数は通常F(x) などのように書きますが、汎関数である事を強調する場合には F[y] のように書かれる場合もあります。
2点間を進むための最小時間と光の屈折
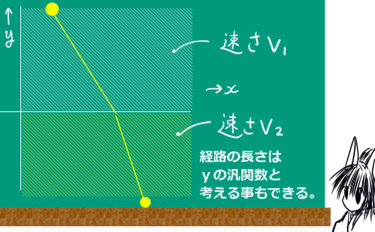
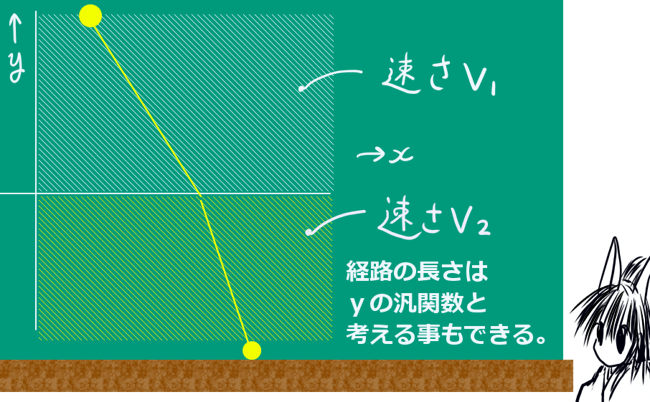
通常の空間(ユークリッド空間)で2点を結ぶ最短距離は、2点間を結ぶ直線の距離です。同じ速さの物体を考える時にも、2点間を進むときの最短の時間となるのは直線軌道を通る時です。
しかし、領域によって速さが変わってしまう場合などは、じつは最短の時間となるのは直線軌道ではなく、折れ曲がったような経路になってしまいます。
どのような折れ線になるのかという問題自体は、普通の微分法で解く事ができます。ただし直交座標の平面を設定して軌道を関数と捉えた場合は関数形が変化して最短距離が決定すると見なせる事が重要で、それが変分の基本的な考え方であるというわけです。
光の屈折は、この問題の結果として表されると考えられています。
【※相対性理論で光線の軌道が曲がるという考え方は、これとはまた少し違った理論なので注意。】
変分の記号と計算
変分を表す時には、δ(デルタ)という記号を使います。これは、微分を表すためにdという記号を使うのと区別する意味があります。
ある汎関数I[y] があった時、 その変分 δ I[y] は、
δ I[y] = I[y+δy]-I[y] で表されます。
(この定義の仕方で考えられた変分を、特に「第1変分」とも言います。)
δy は様々な形の任意の(微小な)関数です。
汎関数 \(I[y]\) に対して $$δ I[y] = I[y+δy]-I[y]$$ \(\delta y\) は様々な形の任意の(微小な)関数。
変分の定義から、例えば2つの汎関数の和ついては
δ( I[y]+J[y] ) = ( I[y+δy]+J[y+δy] ) - ( I[y]+J[y] )= I[y+δy]-I[y] + ( J[y+δy]-J[y] )=δI+δJ
が成立します。差についても同様です。
これらの定義や考え方は、もともとの意味での「微分」がdF(x)=F(x+dx)-F(x) で表される事と似ています。
ただし、微分の場合のdxが(小さい)実数であるのに対して、変分の場合の δy は様々な形の任意の(微小な)関数であり、yと全然違う形の関数も含めて考えているという点が異なります。その意味で、変分と微分は違うものである事は強調されるのです。
一度計算を始めて変化させる関数yを通常の実変数として動かすとみなしてよい状態に持ち込んだ時には微分計算と同じ事ができるという特徴があります。ただし、通常の1変数の微分ではなく、基本的には多変数関数の偏微分を含んだ全微分の計算になる点に注意する必要があります。
例②:解析力学 定積分に対する変分計算
■ 問題の設定 ■ 計算の詳細 ■ オイラー・ラグランジュ方程式
問題の設定
汎関数 I[y] が、次の形
$$I[y]=\int_a^bF(x,y,y^{\prime})dx$$
$$条件:端点 x=a, x=b でyについての変分\delta y=0$$
で表される場合を考えます。y は x の関数であるとします。
積分などがあるといかにも話が複雑になりそうですが、じつは「部分積分」を使って式を簡単にするなど、計算上の利点も一部存在します。
このとき、I[y]の変分 δI[y] は次のように計算します。
計算の詳細
まず定義に従って、 \( δ I[y] = I[y+δy]-I[y]\) ですが、この先がまず第一のポイントで、積分の中身の \(F( x,y,y^{\prime}) )\) については、xは動かさずに、yだけ変化すると考えます。さらに、この時にyの導関数は 「δy に対する導関数」の分だけ増減、つまり (δy)’ だけ増減します。
$$ δ I[y] = I[y+δy]-I[y] = \int_a^b F(x,y+\delta y,y^{\prime}+\delta y^{\prime} ) -F(x,y,y^{\prime})dx $$
続いて、yを通常の実数変数同様に扱えると考えて、積分の中身を全微分と同様に扱えるとみなします。この場合、xは動かしていませんのでdxに相当する項は0になります。
$$ F(x,y+\delta y,y^{\prime}+(\delta y)^{\prime} ) -F(x,y,y^{\prime}) =\delta y \frac{\partial F}{\partial y}+ (\delta y)^{\prime} \frac {\partial F}{\partial y ^{\prime} } $$
$$ δ I[y] = \int_a^b \delta y\frac{\partial F}{\partial y}+ (\delta y)^{\prime} \frac {\partial F}{\partial y ^{\prime} } dx= \int_a^b \delta y \frac{\partial F}{\partial y}dx + \int_a^b (\delta y)^{\prime} \frac {\partial F}{\partial y ^{\prime} } dx $$
次に、yの導関数に対する変分の項について、xに関して部分積分を行います。
$$(\delta y)’ =\frac{d}{dx}(\delta y)$$
の箇所に対して部分積分を適用するという事です。
【このような事ができるのはδyが「関数」であるからという事には一応注意。】
$$2番目の項について: \int_a^b (\delta y)^{\prime} \frac{\partial F}{\partial y ^{\prime} } dx =\left[ \delta y \frac{\partial F}{\partial y ^{\prime} } \right]_a^b- \int_a^b \delta y \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime} } dx =\hspace{5pt} – \int_a^b \delta y \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime} } dx $$
$$ 【∵\hspace{5pt}x=a,x=b で\delta y=0 という前提条件】$$
端点でδyが0になるという条件をつけているので部分積分した後の第1項は0になって消えます。この条件は、要するに端点は固定して関数形を変化させるという意味です。
これにより、δIを改めて書くと次のようになります。
$$\delta I = \int_a^b \delta y \frac{\partial F}{\partial y}dx – \int_a^b \delta y \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime} } dx $$
$$= \int_a^b \delta y\left(\frac{\partial F}{\partial y} – \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime} }\right) dx $$
さて、物理で使う場合は「ここまで変形できればじゅうぶん」という考え方をします。
オイラー・ラグランジュ方程式
上記の条件での汎関数 I[y] に対する変分 δI[y] が0になる条件を考えると、積分の中身の
$$ \frac{\partial F}{\partial y} – \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime}} $$
という部分が0であればよい事が分かります。(δyは「任意の」(微小な)関数である事に少し注意。)
そこで、
$$ \frac{\partial F}{\partial y} – \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime}} =0$$
という形の微分方程式が成立すればよいという事ですが、これは解析力学では座標系によらずこの形で使用できる運動方程式の形として知られていて、少し長ったらしい名称ですが「オイラー・ラグランジュ方程式」あるいは「オイラーの微分方程式」などとも呼ばれます。
通常のF=ma の形の運動方程式はシンプルな形ではありますが、じつは直線直交座標を特別扱いしていて、座標系を例えば極座標に変換しただけで結構面倒で汚い形にと変わってしまいます。
これに対して上記の形の運動方程式は任意の座標系に対してこの形のまま話を進められるという事で、理論的な扱いとしては便利である場合があります。
例③:相対性理論、リーマン幾何学
一般相対性理論、リーマン幾何学で変分を使う例もあります。
1つの例は「測地線」という、曲面上の2点を「曲面に沿って最短経路で」結ぶ曲線に対して成立する式の導出です。この場合、弧長に相当する次の形の汎関数を考えます。
$$ \int_a^b \sqrt{\sum_{i,j=0}^3g_{ij}\frac{dx_i}{dr}\frac{dx_j}{dr}}dr $$
これを直接変分して計算を進めたものを0とおくか、
あるいは積分の中身の関数を上記で得られた微分方程式
$$ \frac{\partial F}{\partial y} – \frac{d}{dx}\frac {\partial F}{\partial y ^{\prime}} =0$$
に代入して計算を進めるかで、結論の式を得ます。どちらの場合も、最初一般の媒介変数rで計算しておいて、途中でrがsに比例するかr=sとおいて式を簡単にする工夫が行われます。