「同じ向きで同じ大きさのベクトル」を、
「始点を基準とした向き」と「大きさ」を変えずに移動させたベクトルの扱いについて説明します。
一般的に、原則的な扱い方は大体決まっているのですが、
書籍等では少し曖昧に説明されている場合もあるので詳しく説明をします。
ベクトルの相等
・・同じベクトルと異なるベクトルの違いは?
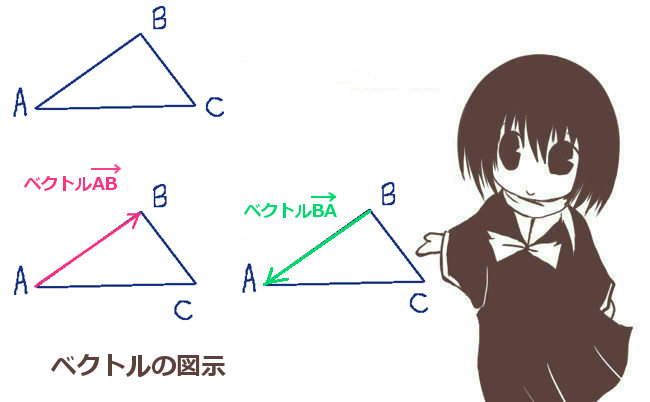
ベクトルの始点と終点を明示した表記方法では、\(\overrightarrow{AB}\) と \(\overrightarrow{BA}\) は異なるベクトルになります。
この事は図形的に見てもそのように言えて、
「大きさは同じ」で「向きが異なる(同一直線上で逆方向)」という異なる2つのベクトルなのです。
さて、ここで問題にしてみたいものがあります。
2つのベクトルが、次のような条件を両方満たす場合です。
- 「向きと大きさの両方が同じ」
- 「しかし、始点と終点が異なる」
例えば、平行線の関係にある異なる線上の2つのベクトルで、大きさは同じで向いている方向も同じという場合です。
それらは、異なるベクトルと考えるべきでしょうか?
図形における線分であれば、異なる端点を持つ線分ABと線分CDは、必ず異なるものとして考えます。そうでないと、図形的に正しい議論ができないのです。
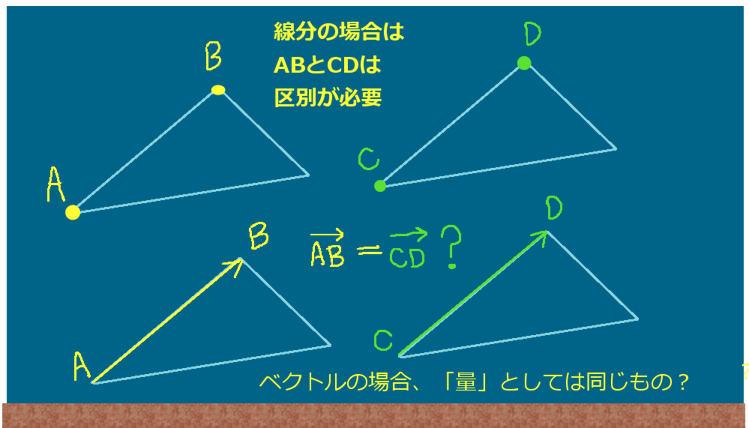
それらは同じで始点と終点が異なる場合は?
では、ベクトルの場合はどうでしょうか。同様に考えるべきでしょうか?
「2つの異なるベクトルが等しい事」を指して数学ではベクトルの相等と呼ぶ事があります。
ここでは、ベクトルの相等が始点と終点の位置に関係するか?
それともそれらには無関係で向きと大きさだけに依存するものか?
という事を考えています。
実のところ、それに対する答えには2つの立場があって扱いが異なるのです。
ただし数学上の考察を含めて一般的に、何の断りもなければ原則としてどちらの立場で考える事が普通であると言う事はできます。
基本的にはベクトルは「自由ベクトル」
ベクトルの場合は、向きと大きさを持つ「量」として考えている事もあって、
実は「向きと大きさの両方が同じ」であれば、「始点と終点が異なる」場合でも同じベクトルであると考えるのです。
特に断り書きが無ければそれが基本的な考え方になります。
ただしそのように考えるベクトルである事を強調して、特に自由ベクトルと呼ぶ事もあります。
自由ベクトルは、向きと大きさを保ったまま自由に動かす事ができます。
(そのような移動を「平行移動」と言います。)
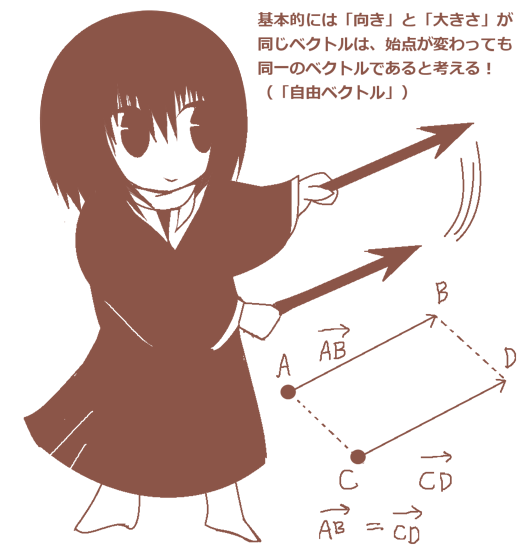
普通、数学的な考察の中で何のことわりもなく「ベクトル」と言ったらそれは自由ベクトルを指しています。つまり向きと大きさを保ったまま始点と終点を変更しても、移動前と移動後のベクトルは等号で結べるという事です。
自由ベクトルとして考える場合には、ベクトルの相等は向きと大きさにだけ依存し、始点と終点の位置には依存しないと言う事もできます。
- 原則として、何も断り書きが無ければベクトルは自由ベクトルとして扱う。
- ベクトルの相等は「向き」と「大きさ」だけで決まり、
始点(および終点)が異なっていても同一のベクトルとみなし、等号で結ぶ事ができる。
例えば「始点が同一である」力ベクトルは合成する事ができて、数式的にはベクトルの合成(足し算と引き算)で考える事になります。すこの時に、片方のベクトルを平行移動させて平行四辺形を作って合成を考えます。つまりその時にはそのベクトルを自由ベクトルとして考えているわけです。
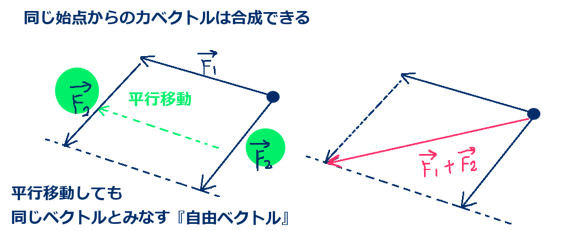
ベクトルに関して数学的な一般論として考察や計算を考える時には、
基本的にはベクトルは自由ベクトルとして考えます。
始点の位置を問題にする「束縛ベクトル」
それに対して、状況によっては始点が特定の場所に固定されていると考える必要がある場合があります。つまり、始点が異なれば別のベクトルとみなす必要がある場合です。そのように考えるベクトルは、特に束縛ベクトルと呼ばれる事があります。
例えば現実に2本の綱があったとしましょう。
それらを2人の人が引けば2つの力ベクトルを考える事ができます。
しかしそれらの力ベクトルの始点(力の作用点)は異なります。
そういった場合に、仮に2つの力ベクトルを平行移動でぴたりと重ね合わせる事ができたとしても、それらを「同一の力」と評するには違和感があります。
その違和感は、ベクトルの始点が異なっている事に由来するのです。
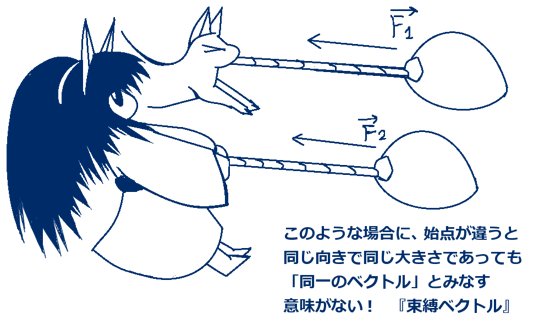
そのような場合でも、力ベクトルの大きさに関して F1 = F2 のように書けます。
束縛ベクトルを考える場合には、
必ずしもベクトルの始点が「同一の点」ではなくてもよい事もあります。
例えば「同一の線上」「同一の面上」であればよいとする事もあるのです。
いずれにしても、ベクトルの始点が具体的にどこにあるのか範囲が限定されているベクトルが束縛ベクトルであり、ベクトルの相等が「向き」と「大きさ」と「ベクトルの始点が存在する位置」に依存するわけです。
ただし、考察対象のベクトルが自由ベクトルであるか束縛ベクトルであるかの区別は、数学的というよりは物理的な解釈により判断する事が普通であると思われます。
例えば異なる物体に作用している複数の力ベクトルであれば、「別々の物に加わっている別々の力なのだから、その時点でベクトルを等号としては結べる事はない」と解釈しても何の支障もありません。
具体的な状況下で複数の束縛ベクトルを考えた場合でも、その時に考えている始点を基準にして限られた範囲で自由ベクトルのように考える事ができます。例えば、ある力の作用点に対して重力と摩擦力が働いている場合には、元々ベクトルの始点は同一である事は大前提にしたうえで、ベクトルを平行移動させてベクトルの「平行四辺形」を考えて力ベクトルを合成するといった計算ができます。
自由ベクトルは始点が原点である場合を基準にできる
始点を原点としてベクトルを考える場合にはベクトルは座標で表すか、終点が分かる文字で代表させる表記方法ができます。
この時には始点が皆共通ですから、向きと大きさが一致すれば終点も必ず一致します。
さてそこで、自由ベクトルとして考えているベクトルでは向きと大きさを保てば自由に移動させて構わないので、始点を原点にそろえる事もできるわけです。
この考え方のもとでは、
平面上あるいは空間内の任意のベクトルは座標を使って表す事ができる事になります。
例えば次の2つのベクトルを考えます。
- 原点を始点とした(1,1)というベクトル
- (2,1)を始点としてx方向とy方向にそれぞれ1ずつ進み、
(3,2)に向かうベクトル
これらは、自由ベクトルとしては全く同一のベクトルとしてみなせるのです。
☆ベクトルの減算を使うと、
2番目のベクトルは(3,2)-(2,1)=(1,1)と計算して表す事ができ、
確かに1番目のベクトル(1,1)に一致する事を見れます。
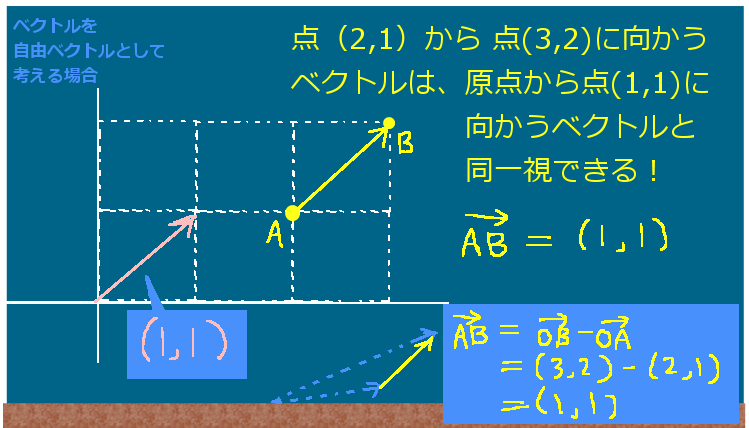
ここでの例で、点(2,1)をAとして、点(3,2)をBとすれば
\(\overrightarrow{AB}=(1,1)\) と書く事ができます。
つまりベクトルを自由ベクトルとして考える前提のもとでは、
\(\overrightarrow{AB}\) のような始点と終点を明記した形のベクトルも、
原点を基準とした座標成分による表記方法と、数学的に等号で結べるという事を意味するのです。
この時には、平面上あるいは空間内の具体的な2点間のベクトルである事を明示しつつ、
「向きと大きさは原点を基準とした時の(1,1)というベクトルに等しい」という事を表現しているとも解釈できます。
- 基本的にはベクトルは自由ベクトルとして考えて、
「向き」と「大きさ」が等しければ、始点の位置によらずに同じベクトルであると考えて等号で結ぶ事ができる。 - 特に断りが無ければ、数学的な計算や考察ではベクトルは自由ベクトルであると考える。
-
ただし物理学等での個別の考察を行っている時には、
始点が限定された範囲内にないと、向きと大きさが等しくても同一のベクトルとはみなせない束縛ベクトルとして実質的に考える事もある。 - ベクトルが自由ベクトルであれば、
始点と終点を明記する表記と原点を基準にした表記は同一視する事ができ、
等号で結ぶ事もできる。
