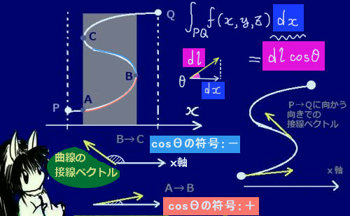
線積分という言葉は、ベクトル場に対する接線線積分と、スカラー場に対する線積分の両方に対して使われます。ここでは、スカラー場に対する線積分についての定義と積分の考え方について説明します。
接線線積分と同様に、スカラー場に対する線積分も電磁気学等での理論計算に使われます。
接線線積分の内積計算を行う過程で、
座標変数であるx、y、zを積分変数とする線積分を考える事もあります。
◆参考(サイト内リンク):
・ベクトルの考え方:スカラーの違い
・定積分の計算と考え方
基本的な考え方
スカラー場 f(x, y, z) に対する「線積分」の基本的な考え方は、次のようになります。
- 積分の対象となる関数がスカラー場(座標成分を変数とするスカラー関数)
- 積分範囲が平面上または空間内の曲線上の経路
積分経路の表記は、ベクトル場に対する接線線積分と同じで、曲線上の2点PとQを決めてPQと書いたり、経路をCなどの名称で表したりします。(その書き方は、積分変数が座標変数が弧長の場合でも座標変数の場合でも、どちらでも同じです。) $$積分変数が弧長の場合:\int_{PQ}f(x,y,z)dl$$ $$積分変数がxの場合:\int_{PQ}f(x,y,z)dx$$ $$積分変数がyの場合:\int_{PQ}f(x,y,z)dy$$ $$積分変数がzの場合:\int_{PQ}f(x,y,z)dz$$
積分変数となる変数は弧長(曲線の長さ)であるとする場合と、
x,y,zの座標成分である場合があります。
どちらの場合でも線積分という語が使われる事が一般的です。
ただし、後述しますように両者で積分方向と積分の符号に関する規定に相違点があります。
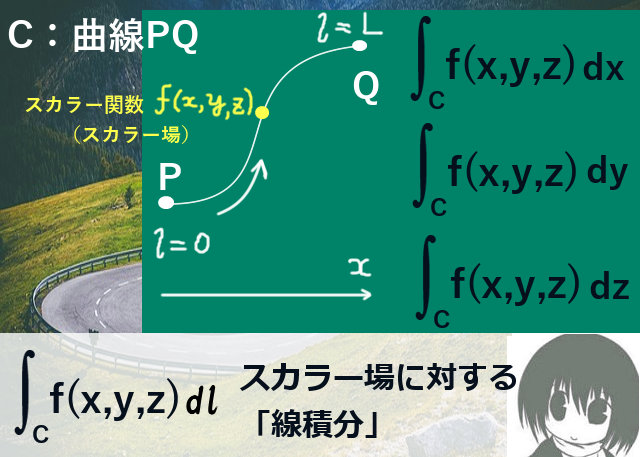
積分変数が弧長の場合と、座標変数x,y,zの場合の両方に対して「線積分」が定義できます。
積分変数が弧長の場合
積分変数が弧長である場合には、積分経路が曲線上の点Pから点Qまでの経路である時に、点Pにおいて弧長が0、点Qにおいてある長さLであるとして積分を行います。
弧長とは「曲線の長さ」の事です。基本的に、折れ線で近似した時の極限値を指しています。
$$\int_{PQ}f(x,y,z)dl=\int_0^Lf(x,y,z)dl$$
ただし、右辺のように表して具体的に原始関数を探して計算するといった場合には、後述するようにスカラー場は \(l\) の関数の形になっている必要があります。
弧長を表す文字としては、sやtが使われる事もあります。
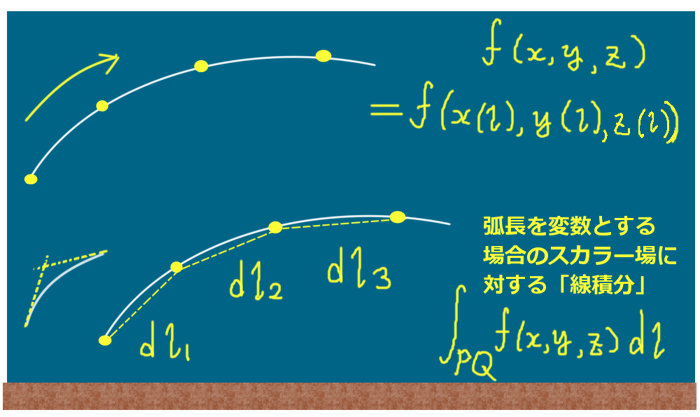
折れ線で近似をして合計し、極限を考えて積分するという考え方です。
この時に弧長は点Pから測って決めているので、
同じスカラー場に対して点Pからではなくて
「点Qから線積分を行う場合」には、積分全体の符号が変わります。
積分の向きと積分全体の符号の関係の考え方は、接線線積分の場合と同様になっています。
$$\int_{QP}f(x,y,z)dl=\int_L^0A(x,y,z)dl=-\int_0^Lf(x,y,z)dl=-\int_{PQ}f(x,y,z)dl$$
このように書けるわけですが、
線積分を具体的な定積分として計算する場合にはx、y、zが弧長を変数とした関数で表されている事が必要な場合が多いです。
すなわち、指定された曲線上の経路では特定の点からの弧長によって点が一意に確定するわけですから、具体的に容易に書けるかは別問題として、理論上は座標変数を弧長の1変数関数として表せるはずであるという事です。
$$x=x(l), \hspace{5pt}y=y(l),\hspace{5pt}z=z(l)\hspace{5pt}であれば$$
$$f(x,y,z)=f(x(l),y(l),z(l))となり、$$
$$\int_{PQ}f(x,y,z)dl=\int_0^Lf(x(l),y(l),z(l))dlとして計算可能になる場合もあります。$$
積分変数が座標変数の場合
積分変数が座標変数x、y、zの場合でも、曲線を経路とする積分を指して「線積分」と呼びます。
この場合には、弧長を変数とする場合やベクトル場に対する接線線積分とは少し考え方が変わります。
まず、積分変数がxの場合を考えてみます。yやzに対しても考え方は同じです。
積分の元々の和としての定義を考えてみると、積分変数をxとするという事は「対象となる関数の値と分割された区間の長さΔxとの積」を合計して極限値をとるはずであり、実際その場合の線積分もそのように定義されるのです。
つまり、曲線上の各点において「曲線の分割された(微小な)経路分のx軸への射影」を考えてスカラー場との積を合計して積分するといった形になります。
$$積分変数がxの場合の線積分の表記:\int_{PQ}f(x,y,z)dx$$
ただし、具体的にxに関する原始関数を探して定積分したい場合には、yとzがxだけの関数で表されている必要があります。
$$具体的な計算をするには、y=y(x),\hspace{5pt}z=z(x)\hspace{5pt}として表されて、$$
$$\int_{PQ}f(x,y(x),z(x))dxの形にする必要があります。$$
◆特定の曲線上の点という条件がある事によって、このようなxだけで表されるy=y(x),z=z(x)のような関数は必ず、存在はします。ただし、そのような関数が簡単な形で書けるかどうかは別の問題になります。特定の曲線上の点を考えるという条件のもとで、x、y、zは独立な変数ではなく、互いに従属の関係にあります。
この時に、曲線の形状によっては単純に1つの積分区間でのxによる定積分としては書けない場合があり、積分をいくつかに分割する必要がある場合があります。
例えば円等の閉曲線では、ある所まではxが増加するように曲線が進んでいき、あるところで逆にxが減少する方向に曲がる事になります。xが減少する方向に積分していく場合には積分の符号も逆向きになりますが、それは通常の1変数の定積分の考え方で符号を考えればよい事になります。
その場合には例えばPQの間にいくつかの適切な点、
例えばAやBを決めて次のように積分を分割します。
$$\int_{PQ}f(x,y,z)dx=\int_{PA}f(x,y,z)dx+\int_{AB}f(x,y,z)dx+\int_{BQ}f(x,y,z)dx$$
この時に、例えばP→Aまではxが増加する方向で、A→Bはxが減少する方向、B→Qで再びxが増加する方向であるなら、yとzがxの関数として表されている前提で、各点のx座標を使って線積分は次のようにも書けます。
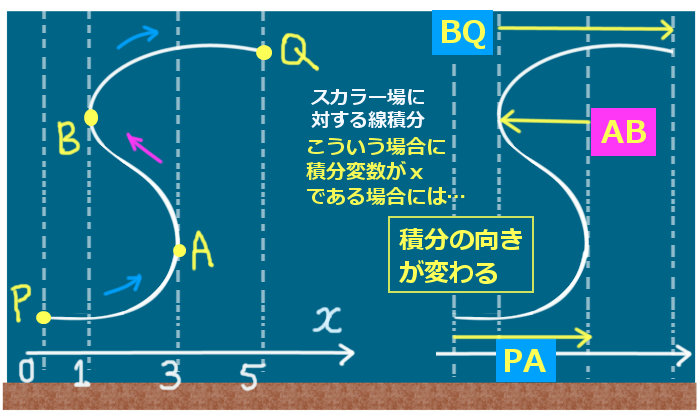
積分する向きと符号に気を付ける必要がある場合もあります。
具体例としてPのx座標が0、Aのx座標が3、Bのx座標が1、Qのx座標が5である場合で線積分を書いてみます。
$$\int_{PQ}f(x,y,z)dx=\int_0^3f(x,y,z)dx+\int_3^1f(x,y,z)dx+\int_1^5f(x,y,z)dx$$
この例の右辺の2項目の定積分は、通常のxが増える方向へのx=1からx=3までの定積分とは符号が逆向きになっているわけです。
$$\int_3^1f(x)dx=-\int_1^3f(x)dx\hspace{5pt}です。$$
これらの符号の扱いについては、分割された区間の(微小な)長さΔxについて、プラスとマイナスの符号を持っていると解釈して定義しておく方法も存在します。
弧長と座標成分の、余弦を使った積分変数の変換
曲線上で積分する方向(弧長が0から何かの値Lまで伸びる方向)を決めたうえで、
「曲線上の各点の接線ベクトルと座標軸のなす角\(\theta\)」の余弦を考えると、
弧長と座標変数との関係を余弦で結ぶ事ができます。
$$角度を\theta として、例えばdx=ds\cos\theta$$
考えているこの角度\(\theta\)は一般的に当然一定値ではなくて曲線上の位置によって異なりますから、
それを明確にするなら例えば \(\theta (l)\) のように書くことになります。
このような考え方は、
積分変数を「座標成分から弧長に変換する」ような場合に使う事になります。
$$例えば、\int_{PQ}f(x,y,z)dx=\int_{PQ}f(x,y,z)\cos(\theta (l))ds$$
この時に、xで線積分するのであれば、曲線の形状によっては
通常のxが増加する向きでの積分に対して符号を入れ替える必要も出てくるわけですが、
弧長を積分変数とする場合には、
点P→点Qに向かう経路である限り一貫して弧長が増加していく方向で積分が行われます。
そこで、上記の余弦を乗じる事によって符号も一致するように調整されるという事になるわけです。
x、y、zを積分変数とするスカラー場に対する線積分は、ベクトル場に対する接線線積分のように内積を計算する事はありませんが、弧長を変数とする場合のスカラー場の線積分からの変換と考える場合には分割した積分の符号の扱いに関しては内積の符号の扱いと同じ考え方をしています。
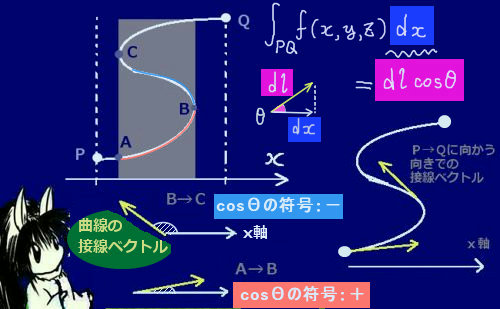
積分変数としての弧長と座標変数の関係を考える事もできます。
この時の余弦の取り方は、内積の計算に似ています。
この考え方のもとでスカラー場に対する2つの線積分の定義の、積分の符号の考え方の整合性が取れます。