実数に関する絶対値の意味と、高校数学の範囲で想定される問題について説明します。
絶対値とは?
■ 実数の「絶対値」の意味
■ 文字式に対する絶対値
■ 絶対値記号がついた関数のグラフ
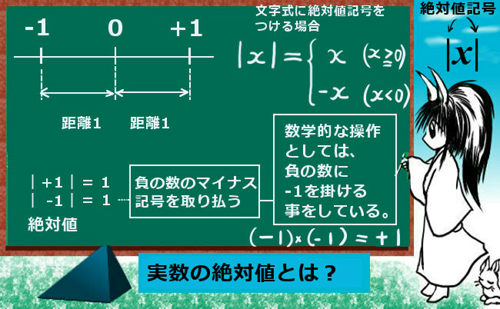
実数の「絶対値」の意味
絶対値とは、意味としては向きに関わらず正の値として特徴づけられる「大きさ」のようなものです。
実数の場合、正の数の絶対値はその値そのもの、負の数の絶対値は符号を取り除いて正の数に直したものを指します。記号は、数を2本の縦棒||で挟んだようなものを使います。例えば次の通りです。
$$実数+3の絶対値\hspace{10pt}|3|=3$$
$$実数-3の絶対値\hspace{10pt}|-3|=3$$
後述もしますが、負の数の「絶対値」は、-1を掛ける事で正の数にしたものでもあります。文字式や関数の絶対値を考える場合は、こちらの考え方のほうが重要になります。
尚、複素数に関しても絶対値というものもあり、ベクトルの場合は絶対値ではなく「大きさ」とか「距離」とか言いますが、記号は実数に関する絶対値と同じ記号を使います。
$$参考:複素数の絶対値\hspace{5pt}|1+2i|\hspace{15pt}ベクトルの「大きさ」|\overrightarrow{AB}|$$
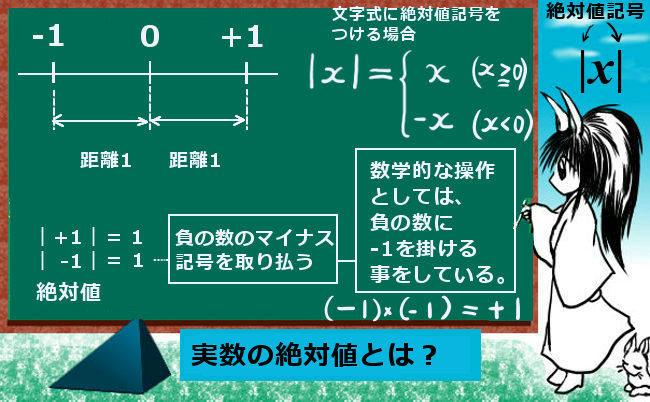
文字式に対する絶対値
さて、という事は実数に関する絶対値というのは要するに正の数だろうが負の数であろうがとにかく符号はプラスにするというものですので、「大した意味を持つものではなく簡単ではないか」という話にもなります。実際、意味自体は簡単である事は事実です。
ただ、高校数学の場合、くせものなのは文字式や関数に絶対値記号をつける場合なのです。
例えば、実数変数xに絶対値記号をつけた |x| については次のように処理せねばなりません。
$$①x≧0 の時、 |x|=x,\hspace{10pt}②x<0 の時、 |x|=-x$$
注意が必要なのは、変数xが「負の数」の範囲にある場合で、絶対値記号を「外す」時にはマイナス記号を添えねばなりません。これは、xが負の数であるのだから、反転して正の数にするためには数学的な操作としてはマイナスを掛ける必要があるという事です。
$$x<0 の時,|x|=-x\hspace{10pt}例えばx=-2なら、|x|=-x=-(-2)=2$$
人間が自分の感覚でやる時には「マイナス記号を取り払う」事で負の数を正の数にできますが、数学的な演算としては負の数を正の数にするには「-1を掛ける」操作が必要であるという事なのです。
より複雑な文字式に絶対値記号をつける場合も考え方は同じで、不等式に関する問題も絡んできます。
$$|A-2B|=A-2B【A≧2B】\hspace{10pt}|A-2B|=-(A-2B)=-A+2B【A<2B】$$
関数に絶対値記号をつける場合は、その関数がどの変数の領域(「定義域」)で正の数になるのか、負の数になるのかという問題が直接的に絡みます。
$$|x^2-3x-4|=|(x-4)(x+1)|から、x^2-3x-4の正負の状況が分かる。$$
$$x≦-1またはx≧4の時、|x^2-3x-4|=x^2-3x-4$$
$$-1<x<4の時、|x^2-3x-4|=-x^2+3x+4$$
このように、絶対値記号とは意味自体は簡単なのですが、出題する問題として話を複雑にしようと思えばいくらでもできるような性質のものでもあるので、いくらか慣れておく必要もあると思います。
絶対値記号がついた関数のグラフ
上記のように関数に絶対値記号をつける事もできるわけですが、この時にグラフを描くと、関数が0の値をとる点を境にx軸に反射するように折れ曲がるグラフになります。
例えば、次の3つの絶対値記号がついた関数のグラフは図のようになります。
$$y=|x|, \hspace{10pt}y=|x-1|, \hspace{10pt}y=|x^2-1|$$
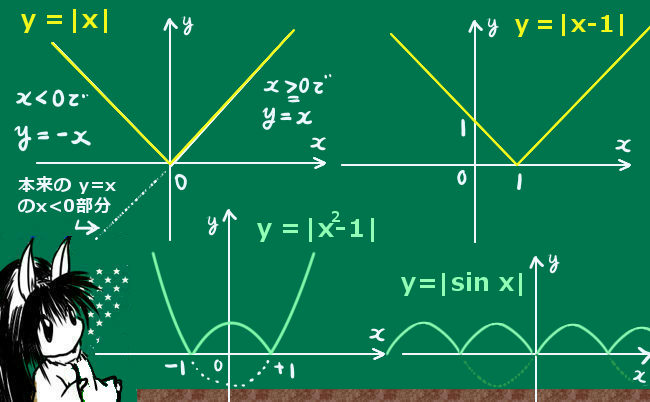
2次関数に絶対値符号をつけた関数に関しては、因数分解する(本質的には解を計算する)事でグラフの形が分かります。
$$x^2-1=(x+1)(x-1)から、もとの2次関数の正負の範囲が分かります。$$
高校数学で問われる事は少ないと思いますが、三角関数に絶対値記号をつけた形の波形のグラフというものも想定できます。通常は負の数の部分が反転して周期的に山がいくつも連なるようなグラフになります。
参考までに、この類の波形は、電圧や電流として正弦関数等を考える時には実際に作れるもので、交流を直流に変換するための古典的な技術の1つです。半導体素子を上手に回路に組み合わせると実現可能となります。
応用:どういった出題があるのでしょう?
■ 直線との交点の問題など ■ 微積分との複合問題
直線との交点の問題など
上述の通り、関数に絶対値記号をつけると、グラフ上では形が変わってしまう場合があります。
そうすると、例えば同じ「2次関数と直線の交点の状況を調べる」という問題であっても、関数部分に絶対値記号をつける事で計算の手間が1つ増えてランクが少しだけ上がるわけです。
$$■問い:直線y=x+Cと図形y=|x^2-5x+4|が3点で交わるCの値は何ですか。$$
こういった問いの場合、少し引っかけどころがあって、x軸に対して反転した部分に「接する」ことで3点で交わるパターンと、ちょうどx軸で反転する1点と、突き破るように関数と交わる他の2点と合わせて3点という場合があります。仮にこういう問題が出題された時には、どちらの場合も述べないと完全な正答にならないところがくせものです。
この問いに関しては、図に描いてみると状況を把握しやすいと思います。
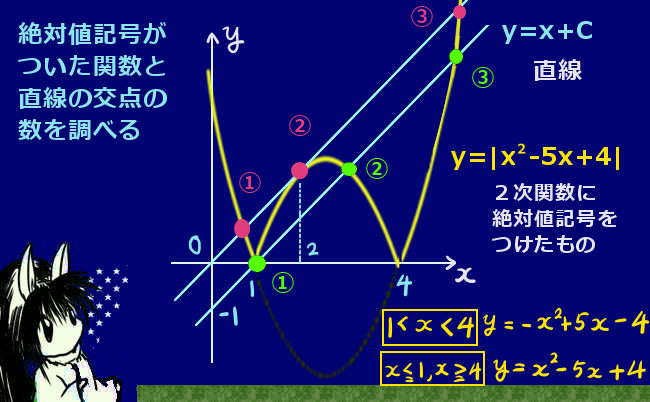
A.まず、2点および接点によって3点で交わるパターンです。
この場合には、接する部分は2次関数の部分が反転していますから、
$$y=x+Cと、y=-(x^2-5x+4)=-x^2+5x-4が接する状況を考えます。$$
$$x+C=-x^2+5x-4\Leftrightarrow -x^2+4x-4-C=0$$
$$\Leftrightarrow -(x-2)^2-C=0$$
よって、ちょうどC=0であればそのような状況になります。これがまず1つです。
B.もう1つの場合。この場合、絶対値記号の中の2次関数が0になる部分の片側(値が小さいほう)を直線が通る事になります。
$$x^2-5x+4=(x-1)(x-4)なのでx^2-5x+4=0\Leftrightarrow x=1またはx=4$$
直線のほうのy=x+Cが、点(1,0)を通ればよいわけです。この場合、y切片であるCを知るのは簡単で、C=-1です。(分かりにくければ図を見てください。)
よって、題意を満たすCの値はC=0,-1です。【解答】
この問いの場合は直線のほうの傾きが固定されているので比較的状況を把握しやすく、逆に傾きのほうが変化する場合には状況はやや複雑になります。さらに、直線の式のほうに絶対値記号がつく場合も同様に複雑になります。いずれにしても、グラフの図形的状況を丁寧・正確に把握する事がポイントとなります。
この問いと同じ部類で、より平易なパターンはx軸に平行なy=Cのような直線と、2次関数が一部反転した関数との交点を調べさせる問題です。その場合、反転した頂点部分より上とx軸で2交点、頂点の座標では3点、x軸から頂点までの間では4点、y座標が負の部分では0点で交わるという事になります。
微積分との複合問題
微積分の問題で、絶対値記号がついた関数の微分や積分を問うという出題も一応あり得るものではあります。いずれの場合も、絶対値記号がついたままでは微分も積分もできません。
まず絶対値の中身の正負の状況を正確に把握して、絶対値記号を外すという操作が必要になります。それから、微積分の操作をします。
上記の2次関数に絶対値記号をつけた関数に直線が接する条件を微分で出す場合には、x軸に対して反転した部分で接するため、マイナスをつけて絶対値記号をはずした2次関数を微分する事になります。微分の場合は、関数の正負が反転する部分は導関数の正負も反転するだけという性質をうまく使える場合もあります。
定積分であれば積分区間を分割する事になります。本来マイナスになる部分の定積分がプラスに転じるので全体の値も当然変わってきます。
いずれにしても、通常の形の関数を微積分するよりも一手間かかる問題になりやすいのです。
参考までに、絶対値記号がついた関数がx軸で反射するように折れ曲がる点は、微積分学では関数が「連続であるけれども微分不可能である」点の例の1つとしてよく取り上げられます。これは、その点に変数xを近づける時に、大きい側から近づける場合と、小さい側から近づける場合とで微分係数に相当する極限値が異なる値になってしまうためです。