高校・大学入試レベルの微積分の問題例です。その中ではやや易しめで、その代わりなるべく「速く・正確に」解けるとよいでしょう。
- 対象となる関数は2次関数か3次関数。
1つの大問の中に微分と積分がどちらもある事が多い。 - 変数以外にaとかbとかの未知の定数がある問題が多い。
- 定積分は基本的に面積計算が多い。2つ以上の関数が関わる事が多い。
「問題を解く事自体」は最終的には計算の作業になるので、重要な事は問題を解くのに使う公式や定理を覚えているかどうかという事と、それらの公式や定理の意味を知っているかどうか、具体的に数値を当てはめる計算ではどのように使えばいいのかがある程度分かっているかどうかという事であると言えます。
微積分の問題で言うと、次の事が重要です。
- 微分と積分は逆演算の関係にある事
- 微分係数は図形的には「接線の傾き」である事
- 定積分は図形的には「面積」を表す事
- 微分係数が0になる点では、その点の前後で微分係数の符号が入れ替わるなら関数は極大値か極小値をとり(これは必ず)、それが最大値あるいは最小値である事もある(これは必ずではありません)
また、グラフ上での直線が直交する条件であるとか(傾きの積が-1になる)、グラフを平行移動をした時の関数の形(xのプラス方向なら f(x)→f(x-c))など、知っておくべき事項もいくつか出てくるでしょう。
次の模擬問題のように、言ってる事自体はじつは何ら難しくないのですが、
ちょっと面倒なものを「手早く」解く必要に迫られるタイプの問題などがあります。
2つの放物線f(x)=ax2-4a2xとg(x)=-ax2+4a2xとがあり、aは正の実数、
f(x)とg(x)のそれぞれの原点における接線は直交しているという。
この時に、y=f(x)の原点における接線とy=g(x)とで囲まれた部分の面積はいくらですか。
まず、微分します。
fのほう:2ax-4a2 →原点で-4a2【x=0】
gのほう:-2ax+4a2 →原点で4a2
【直交するので傾きの積が-1】 ∴-16a4=-1 【a>0に注意して】∴a=1/2
fの原点での接線:y=-4a2x=-x
g(x)の式:g=-x2/4+x 【条件の式にa=1/2を代入】
【交点が必要なので】g=-xとおいて、-x2/4+x=-x
⇔x2-8x=x(x-8)=0 ∴交点はx=0と8
【g(x)が原点を通る事は計算しなくても分かりますが】
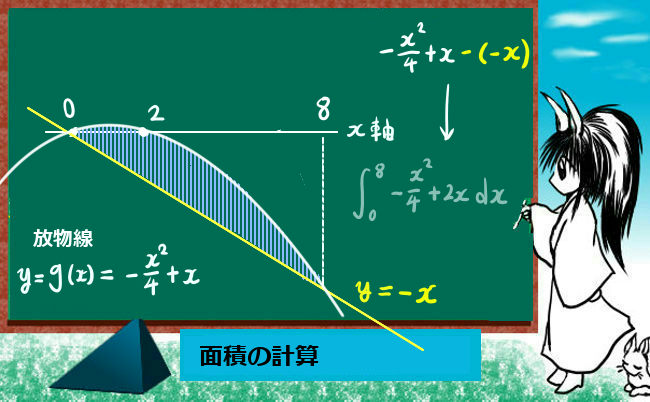
【面積がほしいので定積分します。放物線のほうが上です。一応概形だけさっと描くとよいでしょう。】
積分:-x2/4+2x【-x2/4+x-(-x)】を0から8まで
$$\left[-\frac{x^3}{12}+x^2\right]_0^8 =-\frac{8^3}{12}+64=\frac{-128+192}{3}=\frac{64}{3}【解答】$$
このように解答があまりきれいに約分できない場合というのは結構多くあります。
実際の試験では、例えば途中の交点の計算が小問として穴埋めになっていたりします。
★積分の計算のところで、記述式であればきちんと定積分の記号から書かないとまずいですが、穴埋め形式でしかもほぼ2次関数・3次関数のみ扱われる事を考慮し、ここでは「対象の関数」→「定積分の計算は不定積分に値を代入」という感じで敢えて計算を記しています。
また、ここで記した解答の中で【直交するので掛けて-1】のような部分も、記述式であればきちんと書いたほうがよいですが、穴埋め問題であれば頭の中だけで考えて(考えれるようにして)計算だけ紙に書けば時間短縮になります。
グラフ上の適当な点のx座標をaなどとおいて、そこでの接線の方程式を計算させるタイプの問題も多く見られます。次の例を見てみましょう。
■放物線y=x2上に点P(a,a2) があり、0≦a≦2であるという。
この時にaを動かせるとすると、
点Pにおける接線、x軸、直線x=2、y=x2で囲まれる面積の最大値と最小値はいくらですか。
【微分します。】2x → 2a【点Pでの接線の傾き】
Pでの接線:y=2a(x-a)+a2=2ax-a2
【特定の点を通る1次関数の式です。y-a2をx-aで割ったものが「傾き」2aという式です。】
0=2ax-a2とおくとx=a/2【接線とx軸の交点。次の面積計算で使います。】
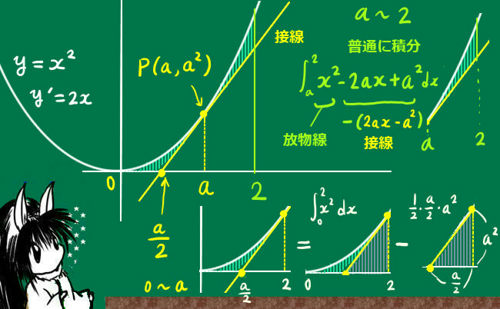
【次に面積計算に移ります。このとき、必要な面積は2つの部分に分けたほうが簡単です。
0からaまでは、「放物線-x軸」面積から「a/2~aと接線」の三角形面積を引くのが簡単です。
aから2までは放物線から接線を引いた部分の普通の定積分です。図を簡易的に描くとよいでしょう。】
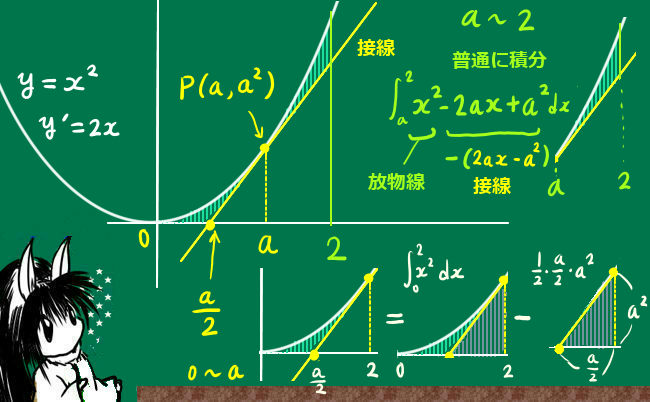
【面積】
①:0からaまで 【放物線・x軸の面積から三角形を引き算】
$$\left[\frac{x^3}{3}\right]_0^a-\frac{1}{2}\cdot\frac{a}{2}\cdot a^2=\frac{a^3}{3}-\frac{a^3}{4}=\frac{a^3}{12}$$
②:x2-2ax+a2を積分:aから2まで 【放物線から接線を引いて積分。a≦2の条件にも注意】
$$\left[\frac{x^3}{3}-ax^2+ax\right]_a^2=\frac{8}{3}-4a+2a^2-\frac{a^3}{3}+a^3-a^3=\frac{8}{3}-4a+2a^2-\frac{a^3}{3}$$
$$合計:\frac{8}{3}-4a+2a^2-\frac{a^3}{3}+a^3-a^3=\frac{8}{3}-4a+2a^2-\frac{a^3}{4}$$
この問題ではまだここで終わらず、面積の「最大・最小」の計算が続きます。
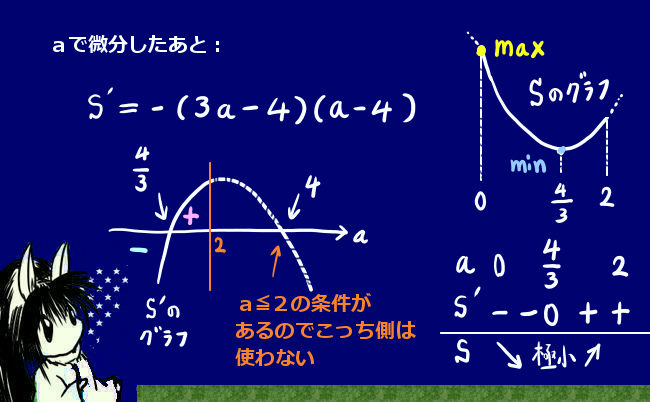
aで微分:-4+4a-3a2/4=-(3a2-16a+16)/4=-(3a-4)(a-4)/4
【aに関して3次関数なので微分して極大・極小を調べます。】
符号に注意して、a=4/3の時に最小【極小でもあります。2次関数のグラフで考えると多少簡単。】
$$最小値:\frac{8}{3}-\frac{16}{3}+\frac{32}{9}-\frac{16}{27}=-\frac{8}{3}+\frac{32}{9}-\frac{16}{27}=\frac{-72+96-16}{27}=\frac{8}{27}【解答1】$$
【こういった分数計算は時間がない中では少し面倒ですが、丁寧・確実に計算する必要があります。】
【最大値も問われてるので調べます。】
aが4まで動ければそこが極大値になりそう? →しかし0以上2以下という条件がある
→ 端点である0と2の値を比べて最大値を見つけます。
【a=4/3で極小という事により、そこから0と2のどちらの方向に向けても増大するので。】
a=0だと8/3、
a=2だと8/3-8+8-2=2/3【これはa=0の時の8/3より小さいので最大値にならず】
∴a=0の時最大、値は8/3【解答2】
この問いは微積の大問と大体同じ分量があるので、10分程度で解答できるとうれしいという感じです。