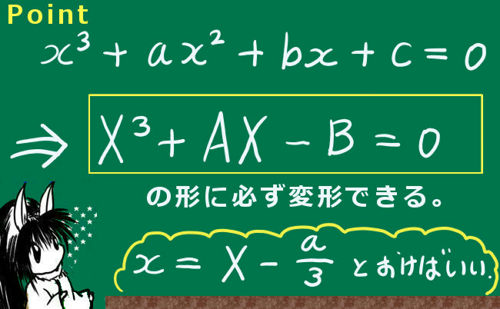3次方程式の「解の公式」の導出方法について説明します。「公式」の導出は、2段階に分けて行います。
一見複雑に見える箇所もあるかもしれませんが、必要な知識は基本的には中学~高校数学程度の式変形です。
①3次方程式の2次の項を、変数の置き換えで消去する
まず、任意の3次方程式は、変数の置き換えによって、ある特別な形の3次方程式に「必ず」変形できる事を示します。(「必ず」というのがポイントです。)
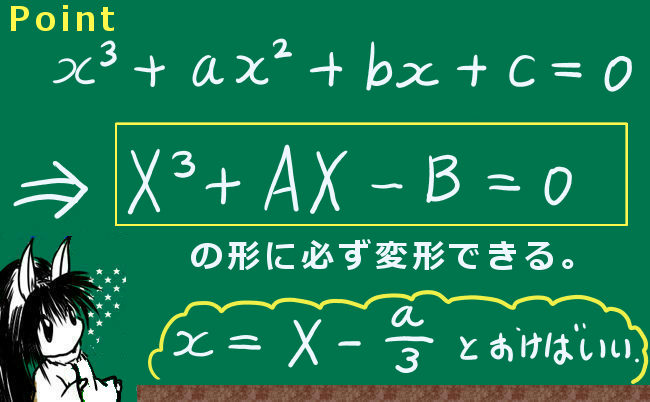
3次の項の係数はそれで式の両辺を割って1にできるのでその後の事を考えます。
$$x^3+ax^2+bx+c=0$$は変数の置き換えにより必ず$$X^3+Ax=B$$の形変形できる。
要するに「2次の項は必ず消せる」という意味です。
x = X + C とします。X に関しても3次方程式になるという形を保つために、X は x に関する一次式である必要があります。
$$x^3=X^3+3X^2C+3XC^2+C^3,\hspace{10pt}ax^2=a(X^2+2XC+C^2) ,\hspace{10pt} bx=b(X+C)$$
2次の項の係数が0であるとすると、
$$3C+a=0\Leftrightarrow C=-\frac{a}{3}$$
とおけば成立します。
$$x^3+ax^2+bx+c=0, \hspace{10pt} x= X-\frac{a}{3} とすると、$$
$$ \left(X-\frac{a}{3}\right) ^3+a \left(X-\frac{a}{3}\right) ^2+b \left(X-\frac{a}{3}\right) +c=0$$
$$ \left(X^3-X^2a+X \frac{a^2}{3}- \frac{a^3}{27} \right) +a \left(X^2-X\frac{2a}{3}+ \frac{a^2}{9} \right) +b \left(X-\frac{a}{3}\right) +c=0$$
$$X^3+X \left( -\frac{a^2}{3}+b \right)+ \frac{2a^3}{27}-\frac{ab}{3} +c=0 $$
ここで、Xに関する係数部分がごちゃごちゃしてるので別の記号AとBで表します。
$$ A=-\frac{a^2}{3} +b , \hspace{10pt} B= -\frac{2a^3}{27} +\frac{ab}{3} -c $$
このように置く事で、
$$X^3+Ax=B$$
の形として方程式を考察できるわけです。
② 3乗の展開式を利用して、解く
さてしかし、この形にしたからといってうまく「解ける」のかという話になります。
これは、じつは3乗に関する展開式についての簡単な式変形によって解く事ができます。
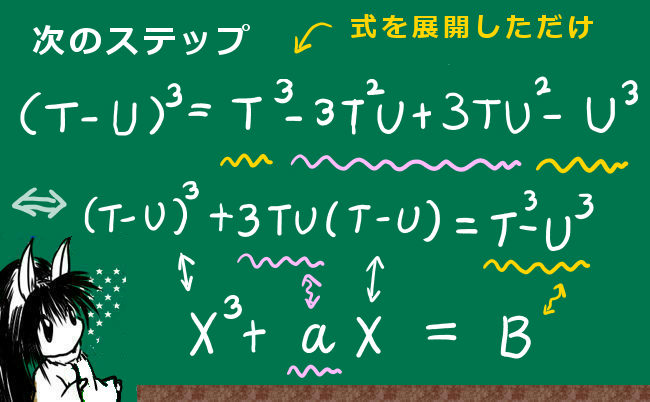
任意の2つの実数(複素数でも可)T,Uに対して
$$(T-U)^3=T^3-3T^2U+3TU^2-U^3$$
$$\Leftrightarrow (T-U)^3+3TU(T-U)=T^3-U^3 $$
この式は、恒等式です。つまり、いつでも成立している関係式です。
これは一体何を意味するのでしょうか?
これは、「次の関係が成立すれば」左辺と右辺が必ず等しくなるわけですから「方程式が成立する」という事です。
$$X=T-U$$
$$A=3TU$$
$$B=T^3-U^3$$
すなわち、これらの関係を満たす X が3次方程式の解になるという事なのです。
もっと具体的には、TとUをAとBだけで表し、X=T-Uに代入すれば XをAとBだけで表せて、それによっておおもとの x が係数 a, b, c のみで表せる・・つまり「解の公式」が得られる、というパズルです。
しかし、上の式を見るとBとT、Uの関係には3乗が入ってます。3次方程式の解の公式が得られていない条件でこれをうまく解けるのかというと、じつは解けます。
$$U=\frac{A}{3T}$$
$$B=T^3-\frac{A^3}{27T^3}$$
$$\Leftrightarrow (T^3)^2-B(T^3)-\frac{A^3}{27}=0$$
このように、「『Tの3乗』の2次方程式」ができるので、これは(無理やり)解く事ができるのです。
結果は、次のようになります。
$$T^3=\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}}$$
$$U^3=T^3-B= -\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}}$$
$$X=T-U= \hspace{5pt} ^3\sqrt{ \frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} }- \hspace{5pt} ^3\sqrt{ -\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} }$$
$$x= X-\frac{a}{3}= \hspace{5pt}^3\sqrt{ \frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} }- \hspace{5pt} ^3\sqrt{ -\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} } -\frac{a}{3} $$
ただし、ここでの3乗根の記号は複素数の範囲も含めた3つの数を取りえるものとします。3次方程式は、複素数範囲まで考え、重解を2解と数えると必ず3解を持ちます。 その事が、3乗根によっても表現されるわけです。
■ 補足:
尚、A=3TU の関係も成立していますから、T か U のどちらかが決定すればもう片方も決定します。これによって、「3×3=9通り?」の解ではなくて、確かに「3通り」の解が存在する事が公式でも表せているというわけです。3解のうち2つが重解として等しい値になる場合は、上記で『Tの3乗』に関する2次方程式が重解を持つ場合に対応します。
3次方程式の解の公式を知る意味:数学史的な価値
さて、このようにして「解ける」事は確かに言えるわけですが、色々置き換えがあって、公式としては代入するだけでもすごく面倒ですね。そういうわけで、物理や工学で仮に3次方程式を解く場面があったとしても、できる事ならこの公式使いたくないわけです。実質的には「手計算で解くなら2次方程式まで」と、基本的には思ってよい理由です。
このように、公式が存在する事と、それが応用の場面等で使いやすいものか・便利なものかという事は、別問題である事もあるわけです。
では、純粋数学的に考察した場合はどうかというと、この3次方程式の解法は、4次方程式については似た事ができます。しかし、5次以降は使えないのです。つまり、「3次や4次については適用できる」という特別なものになります。多項方程式について純粋数学的に一般的に考察する時は、より抽象的な考察が必要であるという事です。
この3次方程式の「解の公式」の解法の話は、大学数学においてはむしろ数学史の中で扱われる事が多いです。というのも、西欧で「複素数」というものが考察されるきっかけになったのがこの3次方程式の解法であると言われているからです。(※2次方程式ではなく3次方程式の解法というところに、数学史的に指摘しておくべきポイントがあるという事です。)
ちなみに数学史的には、この3次方程式の解の公式が「発見」されたのは16世紀という意外に遅い時期であり、しかし4次方程式の解の公式はその後に割とすぐ見つけられて、その後「5次方程式の解を一般的に係数のベキ根によって表す事はできない」という事が示されたのは19世紀まで飛びます。
歴史というか数学の研究史としては、そのような事も1つの教養的知識として多少知っておいてもよいのではないかと思います。
また、数学史的な事についてもう1点補足しますと、16世紀に「解の公式」が見出された時には、解法の流れは上記の方法と同じですが考え方として別の考察の仕方をしていました。それは、上記のように式を展開して関係式を導出するよりも、図形的な考察から関係式を導出していたという点です。
この場合、図形は図形でも、平面図ではなく立体の体積に関する考察です。立体ですから、体積に関して3乗を使うというわけです。参考までに、次図を記しておきます。
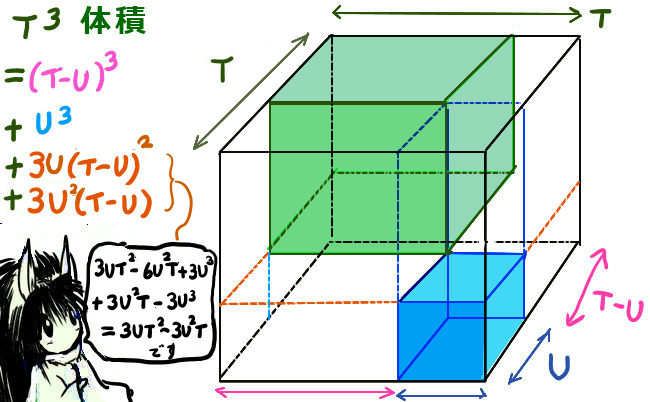
直方体部分は、TU(T-U)などによっても計算できます。