このページでは複素数の微分について述べます。
大学数学では複素関数論(あるいは単に「関数論」)と呼ばれる領域です。
数学上の理論でも応用でも重要なのはむしろ複素数の「積分」のほうですが、面倒なのも積分のほうです。
まず基本的な考え方として微分のほうをここでは説明します。
複素数の微分・・実数の時と何が違う?
まず、具体的な初等関数を微分するレベルにおいては実数の時とほとんど同じです。
■ 定義域が複素数の初等関数の微分・・実数の時とほぼ同じ
■ テイラー展開・マクローリン展開も同様に可能
■ 複素関数論に特有の議論はあるの?

別の数学的考察が必要になる部分のポイントをこのページでは説明します。
定義域が複素数の初等関数の微分・・実数の時とほぼ同じ
複素数を定義域 (変数の範囲)および値域(関数の値の範囲) に持つ関数を複素関数といます。複素関数の微積分を扱う数学の領域を複素関数論(あるいは略して「関数論」)とも言います。複素関数に対して、通常の実数の範囲の関数を「実関数」と呼ぶ事もあります。慣習で、複素関数の変数は x ではなく z で表す事が多いです。ただし、定義域が複素数範囲である事を明示すれば本質的に何の文字を使おうが間違いではありません。
結論を先に言うと、初等関数の定義域を複素数に拡張したものを微分してできる導関数は、定義域が実数の時と同じです。
初等関数に関しては、実関数の時と同じ形の次の公式が成立します。
$$\frac{d}{dz}z^r=rz^{r-1}$$
$$\frac{d}{dz}e^z=e^z$$
$$\frac{d}{dz}\cos z =-\sin z$$
$$\frac{d}{dz}\sin z = \cos z$$
$$f(z)g(z)=\frac{df}{dz}g(z)+\frac{dg}{dz}f(z)$$
その他、実関数に関する公式は大体そのまま成立します。
また、微分の記号も全く同じものを使用します。
★じつのところ、理論として高校数学から直ちに飛びつけない部分は、例えば指数関数や三角関数の場合に「複素数が変数の時にはどういう値をとるのか・・?」という事です。
例えば、cos(2i) などは、ちょっと何の値になるのか(何の値にすべきなのか)分かりませんね。
これについては「複素数の指数関数表示」が大いに関わります。このページでは、個々の関数の定義域の拡張方法についてはとりあえず置いておき、複素関数の微分の全体像について解説します。
テイラー展開・マクローリン展開も同様に可能
初等関数に対して微分が実関数の時と同じ演算で可能という事は、高階微分も同じ計算になるはずで、実際そうなります。そして、初等関数の定義域を複素数に拡張した時も、実関数の時と同様にテイラー展開やマクローリン展開が可能なのです。
例えば、定義域が複素数であっても、三角関数や自然対数の底の指数関数は次のようにマクローリン展開ができます。
$$\sin z=z-\frac{z^3}{3!}+\frac{z^5}{5!}-\cdots$$
$$e^z=1+z+\frac{z^2}{2}+\frac{z^3}{3!}+\cdots$$
※解析学的に、極限の事を厳密に考えていくと実関数との違いは考察として必要になります。その基礎の1つについては後述します。
複素関数論に特有の議論はあるの?
さてこれらの「結論」を見ると、結局複素数の微分というのは定義域を複素数にまで伸ばせばいいだけの話で、数学的にあまり考察する意味はないのでは・・?と、思われるかもしれません。
とりわけ、数学の応用を考える場合はそう思うかもしれませんね。
そこで次に、複素関数の微分において、実関数と違う考察が必要な点を次に述べましょう。これは、複素数の積分のほうを考える時に必要な知識の1つにもなります。
具体的には偏微分を使った考察を行う事になります。実数関数の場合には2変数以上を扱う時に限り偏微分についての考察も必要だったわけですが、複素数を扱う時にはx+yiという形で常に2変数扱うとみなす事もできるので、偏微分も(および全微分も)初歩的な段階から考察対象になるのです。
ただし前述のように、常に2変数と偏微分等を考えないといけないという事ではありません。複素数zを1かたまりとみて1つの変数扱いにできる場合も確かにあるわけです。そこの使い分けが、確かに実数関数の場合と比べて少しトリッキーです。
複素関数の微分の数学的な考え方の詳細
まず微分以前の話として、複素関数というものは実部と虚部という2つの実数部分から、別の複素数の実部と虚部ができるという多変数の関数の一種として考える必要が本来はあります。その考え方をもとに、複素数の微分を改めて捉えてみましょう。
■ 複素関数の実部と虚部はともに2変数関数
■ 複素関数で成立する偏微分の公式(コーシー・リーマンの式)
■ 「正則」という考え方
複素関数の実部と虚部はともに2変数関数
ある複素数 z = a + bi を2乗するという関数を考えてみると、
$$z^2=(a+bi)^2=a^2-b^2+2abi$$
ここで、結果の式の実部を u、虚部の実数部分を v とすると、u は a と b の関数、v も a と b の関数になります。まず、この考え方が重要です。
つまり、一般の複素関数については次のように考えます。
$$z=x+yi\hspace{3pt}に対して \hspace{3pt}F(z)=u(x,y)+iv(x,y)$$
もとの複素数が変数の時、それが2つの実変数から構成されていて、それらから2つの別の2変数関数が構成されて新しい複素数を作るというわけです。
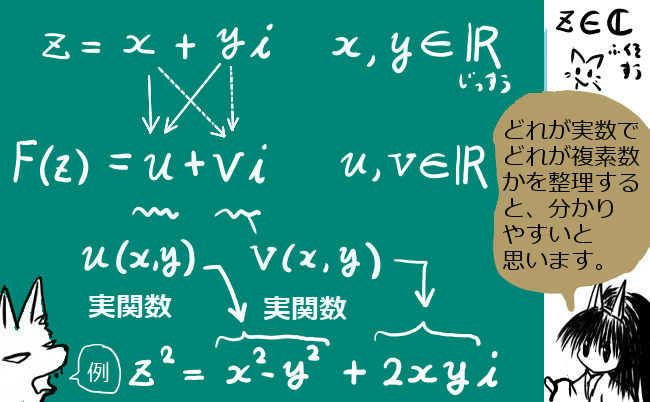
u, v ともに、x と y による2変数関数 u(x,y) , v(x,y) になります。
z は複素数(変数)、F(z) は「複素関数」です。
多変数関数(ここでは必ず2変数ですが)が出てくるところが、
次に述べる複素関数論での偏微分の使用との大きな関わりがあります。
複素関数で成立する偏微分の公式(コーシー・リーマンの式)
実関数の場合の微分のもともとの考え方は、dy = (dy/dx)dx という、近似の「一次式」を新たに設定する事でした。では、これが複素関数の時はどうなるでしょう?
次のように考えます。
まず、導関数および微分係数も複素数で表されると考える事が重要です。
$$\frac{dF}{dz} =\alpha +i\beta \hspace{10pt}【\alpha と\beta は実数(関数)】$$
$$z = x + iy ,\hspace{5pt} dz = dx + idy, \hspace{5pt} F(z) = u + iv $$
$$dF=\frac{dF}{dz}dz=( \alpha +i\beta ) ( dx + idy) =(\alpha dx -\beta dy)+i(\beta dx + \alpha dy)$$
計算は、複素数の四則演算をしているだけです。実部と虚部に分けます。
次に、
$$F = u +i v = u(x,y) + i v(x,y) に対して dF = du + i dv$$
であるとすると、du と dv は次のようになるわけです:
$$du = \alpha dx -\beta dy,\hspace{10pt} dv =\beta dx + \alpha dy $$
さてここで、dF に対する du と dv は「全微分」でも表せるものとして定義します。(そういうものとして「複素関数の微分」を考えようという事です。)すると、
$$du=\frac{\partial u}{\partial x}dx+\frac {\partial u}{\partial y}dy,\hspace{10pt} dv=\frac{\partial v}{\partial x}dx+\frac {\partial v}{\partial y}dy $$
とも表せるわけです。これを見ると、\(\alpha\) と \(\beta\) は、2通りの方法で表せるはずであり、
$$ \alpha= \frac{\partial u}{\partial x} =\frac {\partial v}{\partial y} ,\hspace{10pt} \beta=-\frac {\partial u}{\partial y} = \frac{\partial v}{\partial x} $$
この偏微分に関する関係が、複素関数の微分における特徴的な性質になります。
$$ \frac{\partial u}{\partial x} = \frac {\partial v}{\partial y} ,\hspace{10pt} -\frac {\partial u}{\partial y} = \frac{\partial v}{\partial x} $$
この関係式を「コーシー・リーマンの式」と言う事もあります。
名前よりも数学上重要な事は、複素関数が「微分可能」であるとは、
これら2つの偏微分に関する等式がともに成立するという事なのです。(必要十分条件です。)

尚、特に積分のほうで考え方として重要なのですが、どういった「経路」に沿って微積分をするのかという事も複素関数論では考えます。
その経路とは、例えば直線であるとか円であるとかいったもので、z = x + iy において、x と y の関数で表す事ができます。(例えば直線なら y = 2x など。)
そのような場合には、x と y は完全な独立関係にある変数ではなく、従属関係になります。
従ってその場合には、媒介変数tを使って x = x(t) , y = y(t) を考える事ができます。そうなると、x と y を変数とする2変数関数 u(x,y) と v(x,y) はもとの変数を tとした合成関数と考える事ができます。
そのように考えると、上記のように複素関数の微分において全微分の考え方を使って定義をする事の意味も多少分かりやすくなるかと思います。
この偏微分に関する「コーシー・リーマンの関係式」は複素関数の積分のほうでむしろ重要になる事があり、例えば複素関数についてのコーシーの積分定理を導出する際に必要になります。
「正則」という考え方
上記の偏微分に関して成立する公式の他に、複素関数の微積分では「正則」という考え方も重要になります。これは、微積分をする対象の関数に1つの条件を課す事であり、基本的に複素関数論はその条件をつけた範囲内で理論を組み立てる事が多いです。
dz = dx + idy を考える時に、じつはある点を基準に考えた時に x と y をどのように動かすのかという問題があります。じつのところ、複素関数論では「どの方向に動かしたとしても」極限が一致する事を「微分可能」であると呼びます。(初等関数の微分ではその要件を満たします。)
$$\lim_{h\to 0}\frac{F(z+h)-F(z)}{h}\left(= \lim_{dz\to 0}\frac{F(z+dz)-F(z)}{dz} \right)$$
によって微分による導関数を定義するのは実関数の時と同じですが、「hの部分も複素数」であるところがじつはポイントであるわけです。
これらの事を踏まえたうえで、「1つの点を含む領域の任意の点」で微分可能な(小さな)領域が存在する時、その複素関数はその点で「正則」であると呼びます。また、複素関数が正則である領域においてはその関数は「正則関数」であると呼ばれます。数学の複素関数論の中では、多くの場合に微積分の対象をこの正則関数に限定する事で理論を組み立てているので、用語としては重要です。
文章の表現としては定義の仕方はいくつかあるのですが、ここではその1つを記します:
- ある複素関数 F(z) と、ある点 z = z0 について、z0 を含むある領域で、「その領域内の任意の点で微分可能であるような」ものが存在する時、F(z) は点 z0 において正則であると呼ぶ。
- ある領域の任意の点で F(z) が正則である時、その領域内で F(z) は「正則である」あるいは「正則関数である」などと言う。

