このページでは、高校で教わる範囲の積分公式についての、
やや理論的な一般的性質と式表現の一部について詳しく説明します。
(英:微積分学の基本定理 fundamental theorem of calculus)
目次:
- 積分は微分の逆演算という関係
- 不定積分
- 定積分の公式(部分積分と置換積分)
積分は微分の逆演算という関係
■ ここでは、合わせて原始関数についての説明も続けてしています。
微積分学の基本定理の数式表現
「微分操作の逆演算は積分操作」というのが微積分学の基本定理の内容です。表現の方法はいくつかありますが、てきとうな定数を c として$$\frac{d}{dx}\int_c^xf(t)dt=f(x)$$という表現をするのが、1つの形です。(※変数の表記方法に注意してください。関数としての変数は、あくまで x です。)「ある関数の積分を微分すると元の関数」という事実の表現という事です。$$\int_c^xf(t)dt$$ という表現は、「定積分で積分区間の片方の端の値を変数と考えた場合」の事を言っているのですが、
分かりにくい場合、$$S(x)=\int_c^xf(t)d$$ とおくと、少し見やすくなるかもしれません。
積分区間の片方の端の値 a は固定して、右側の値をずずずっと変化させると「面積」の値も変わります。変化させる「右側の端の値」を変数 x として、面積である定積分を関数 S(x) として考えているわけです。
後述する「不定積分」の形で微積分学の基本定理を表す事もできます。
その場合の表記は、$$\frac{d}{dx}\int f(x)dx=f(x)$$ です。
■ 微積分学の基本定理の証明(このページ内リンク)・・考え方としては、かなり平易です。
「原始関数」とは?
\(S(x)=\int_c^xf(t)dt\) とおく時、微積分学の基本定理は\(\frac{d}{dx}S(x)=f(x)\)とも書けて、
S(x) は「微分すると f(x) になる関数」と見る事もできます。
このように\(\frac{d}{dx}G(x)=f(x)\)を満たす G(x) を f(x) の「原始関数」と言い、
\(S(x)=\int_c^xf(t)dt\)は、f(x)の「原始関数の『1つ』」です。
この時、任意の定数 C を用いて S(x) + C もf(x)の原始関数なのです。(※定数を微分しても0なので。)
この任意の定数 C は「任意定数」「積分定数」などと呼ばれます。
定積分は原始関数で表せる
さて、この\(S(x)=\int_c^xf(t)dt\)に具体的な値 x = a, b を代入する事を考えます。
\(S(a)=\int_c^af(x)dx,\hspace{10pt}S(b)=\int_c^bf(x)dx\) であるわけですが、
(※積分区間に変数 x を含んでいないので dt ではなくdx 表記にしています。また、積分区間の端点が定数であれば、定積分は x の関数ではなく、あくまで何らかの「定数」になる事にも注意が必要です。)
積分する方向と符号との関係、および積分区間の合算の事を考えますと、$${\small S(b)-S(a)=\int_c^bf(x)dx-\int_c^af(x)dx=\int_c^bf(x)dx+\int_a^cf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx}=\int_a^bf(x)dx$$
となり、[a, b] 上で関数を積分する定積分が 「S(b)-S(a)」で表される事を意味するのです。(c というてきとうな定数は、中間点にあるものと考えて、定積分の値には影響しないというわけです。)
そして微積分学の基本定理によれば、S(x) は「f(x) の原始関数(の1つ)」
です。
原始関数同士の引き算を考える場合、(S(b) + C) – (S(a) + C) = S(b)-S(a) となり任意定数は必ず消える事に注意すると、
[a, b] 上で f(x) を積分して得られる定積分は、
原始関数(=微分するとf(x)になる関数) S(x) を用いて次のように表せます:
$$\int_a^bf(x)dx=S(b)-S(a)$$
そして、このS(b)-S(a)の事を通常、次のように書くのです。
$$S(b)-S(a)=\left[S(x)\right]_a^b $$
この記号を用いると、
$$定積分は\int_a^bf(x)dx=\left[S(x)\right]_a^b と表されます。$$
この表現方法が、数学の理論でも物理でも、通常用いられる定積分の計算になります。この意味で、面積としての積分の考え方も重要なのですが、同じく重要なのが「微分と関連付けされた積分演算」というわけです。
積分の変数を dx ではなく dt などに変えるのはどんな場合?
上記の微積分学の基本定理の形では、積分区間(積分する閉区間)に x という変数が入っていて、その x を微分をしています。このような時、f(x)dx については数学では一般的に、f(t)dt などのように、文字を変える決まりになっています。
物理の本などでは「\(\int_a^x f(x)dx\)」のような表記がしてある事もありますが、一応数学的にはあまり良くないので、このサイトでは一般的な数学の決まりに従って積分区間に変数がある時は\(\int_a^x f(t)dt\)のように記します。(記号として t を用いると「時間」と紛らわしい場合は、適宜ギリシャ文字の τ で代用するなどして対応します。)
導関数(関数の微分)を積分すると?・・もとの関数に戻る!
微積分学の基本定理を、ある関数の導関数(ある関数の微分)に適用すると、
「微分したものを積分すると元の関数になる」事が言えるので、微分と積分の関係がより明確になるかと思います。この関係は、微分方程式論で重要です。
$$\frac{d}{dx}\int_c^xf^{\prime}(t)dt=f^{\prime}(x)\hspace{10pt}しかしf^{\prime}(x) の原始関数は f(x) + C に他ならないので $$
$$\int_c^xf^{\prime}(t)dt=f(x) + C$$
微分方程式論においては、任意定数 C というオマケを、任意ではなく「特定の」値に決定するための処理をします。
これは、例えば具体的な f(0) = 0 などと言った値が(1つでも)決まれば C の値も決まるので、積分操作によって関数が1つにきちんと定まるというものです。
原始関数の例
例えば、sin x の原始関数は – cos x + C です。定数を微分するとゼロになるので、原始関数としては任意の定数として積分定数がオマケとしてくっついてくるわけです。cos x の微分は -sin x なので、「マイナス符号を消す」ために -cos x を考えている事に注意してください。
また、\(x^2\) の原始関数は、\(\frac{1}{3}x^3+C\) です。
3次の単項式を微分すると2次の単項式にはなりますが、3 という係数もくっついてくるので、それを「消す」ために 1/3 が原始関数としては必要になるわけです。
このへんが、微分と比べて積分の計算が面倒な点ですが、微分の公式さえあればパズル感覚でも行けるのではないかとも、思います。
微積分学の基本定理から、原始関数を使って定積分を計算する手順
- f(x)の原始関数を、任意定数に関しては何でもいいから探す。普通は、任意定数がゼロのものを考えます。(それが一番簡単なため。)
例:\(e^x の原始関数で加える定数を0としたものは e^x\) - 積分する閉区間の端点を代入し、大きい値を代入したものから小さい値を代入したものを引きます。
例えば e の指数関数を x = 0 から 1 まで積分すると、次のようになるのです。
\(\int_0^1e^xdx=\left[e^x\right]_0^1=e^1-e^0=e-1 (=1.718・・)\)
「不定積分」とは?・・任意定数が含まれる形の積分
定積分に対して、「不定積分」という言葉も微積分学ではよく使われますので、少し説明いたします。
「不定」という表現には、ある関数の原始関数は
「制限をかけなければ任意定数がおまけとして必ずくっついてくるので『1つには定まらない』」
・・という事と、大いに関係があります。
この「不定積分」という用語の数式としての定義は人によって少し違う事もあるので、2つ述べておきます。意味するものは、どちらも大体同じです。
「不定積分」の表し方①・・原始関数全体
まず1つの表し方は、ある関数の原始関数全体を「不定積分」と呼ぶものです。
つまり、何か適当な原始関数 F(x) と、それに任意定数 C を加えたものを不定積分と呼び、次の記号で表します。
$$関数 f(x) の「不定積分」\hspace{10pt}\int f(x)dx=F(x)+C$$
記号としては、定積分の「区間を表す部分」を取り去った記号を使います。
(確かに、原始関数という観点からは、具体的な積分区間については形式的なものであり、明記する意味がそれほどないのも事実かもしれません。)
このサイトでは、特に理由が無い場合は不定積分と言ったらこちらの意味で使わせていただきます。
この不定積分の表記を用いて微積分学の基本定理を表現する事もできます。
F(x)+C を微分すれば f(x) ですから、同じ意味の数式を表せます。
$$不定積分を用いた「微積分学の基本定理」\hspace{10pt}\frac{d}{dx}\int f(x)dx=f(x)$$
「不定積分」の表し方②・・積分で表された原始関数の1つ
他方で、微積分学の基本定理\(\frac{d}{dx}\int_c^xf(t)dt=f(x)\)で用いられている、
\(\int_c^xf(t)dt\)の事を「不定積分」と呼ぶ場合もあります。
この場合は、不定積分とはあくまで、f(x)の「原始関数の1つ」という位置付けになります。また、積分区間に変数を含まない定積分が何らかの「定数」であるのに対して、不定積分は「x の関数」である事が、この後者の表現では明確になるという指摘もできます。
どちらを「不定積分」と呼んでも、他の理論にはそれほど影響はないと思われます。
※この後者のほうの表現は、これを不定積分と呼ぶか呼ばないかに関わらず微積分の理論でよく使用します。
定積分の公式・・置換積分と部分積分
定積分に関しての公式で、大学数学や物理でも知っておくと便利なのは3つほどに厳選できるかと思います。その他、符号や積分区間に関する定積分の基本的な規則などについても合わせてこの表でまとめておきます。
知っておくと便利な公式の1つは、前述の微積分学の基本定理です(不定積分の公式としても表せます)。
2つ目は置換積分の公式で、これは合成関数の微分に関係する積分公式です。
3つ目は部分積分という公式で、こちらは積の微分公式に関係します(これも、不定積分版の公式があります)。
つまり、これらの公式はいずれも微分とつながっています。
| 定積分の公式 | 公式の内容 | 証明・導出法の概略 |
|---|---|---|
| 置換積分 | \(x=x(u), a=x(p), b=x(q)の時、\) \({\large\int_a^b f(x) dx=\int_p^q f(u) \frac{dx}{du}du}\) |
合成関数の微分をもとに示します。詳細 |
| 部分積分 | \({\large\int_a^b f^{\prime}g dx=[fg]_a^b-\int_a^b fg^{\prime}dx}\) ※不定積分として、次のようにも書けます: \({\large\int f^{\prime}g dx=fg-\int fg^{\prime}dx}\) |
積の微分公式を変形して示します。詳細 |
| 積分区間の合成 | \({\large\int_a^bf(x)dx+\int_b^cf(x)dx=\int_a^cf(x)dx}\) | これらは、定積分の定義から分かります。 定積分と面積の関係から、図で理解してもよいと思います。 |
| 積分する方向と 定積分の符号 |
\({\large\int_a^bf(x)dx=-\int_b^af(x)dx}\) | |
| 1点だけの区間 の定積分は0 |
\({\large\int_a^af(x)dx=0}\) | |
| 定積分の線形性 (定数倍など) |
\(c を定数とすると {\large\int_a^b(cf(x))dx=c\int_a^bf(x) dx}\) \({\large\int_a^b(f(x)+g(x))dx=\int_a^bf(x) dx + \int_a^bg(x) dx}\) | |
| 微積分学の基本定理 | \({\large\frac{d}{dx}\int_c^xf(t)dt=f(x)}\) ※不定積分として、次のようにも書けます: \({\large\frac{d}{dx}\int f(t)dt=f(x)}\) |
積分の定義から、 S(x+h) = S(x) + S(h) となる事を使い、微分の定義式に当てはめます。詳細 |
置換積分は、例えば直交座標上で表された関数を「極座標」で表して積分したい時に使います。 例えば、x = cosθ と変換して積分も行う場合です。この時、次の2点を忘れないようにしないと、積分の結果が変になるので注意が必要です。
- 変換した変数での微分:\(\frac{dx}{d\theta}=\frac{d}{d\theta}\cos \theta =-\sin \theta\)
- 積分区間の端点の変換:例えば x について [0, 1] で積分するなら、θ については\(\left[\frac{\pi}{2}, 0\right]\)で積分
※一見積分する区間が変になるようですが、この区間での積分で正しい結果が出るのです。
部分積分は、原始関数が分かりにくい関数について適用します。
例えば、ln x の原始関数は、微分の公式集を見ると見当たりません。(※このページの前半の「積の微分公式」のところに記載があります。)
そこで、ln x に「『1次の単項式 x の微分(=1)』が隠された形で掛けられている」・・と見て、部分積分を適用すると、うまく積分ができるのです。
$$\int \ln x dx= \int (x)^{\prime}\ln x dx=x\ln x – \int x(\ln x)^{\prime}dx=x\ln x – \int x\frac{1}{x}^{\prime}dx=x\ln x – \int 1 dx=x\ln x – x + C$$
また物理では、無限遠(じゅうぶん遠くと見なせる範囲)で関数がゼロになるときに、部分積分を利用した式変形を行う時があります。その場合は、原始関数を知りたいわけではなくて利用しやすいように式の形を変える事に利用しているわけです。
不定積分と原始関数の一覧表
次に、主要な初等関数の不定積分、原始関数の一覧の表を記します。もちろん、積分区間の端点の値を代入する事で、これらは全て定積分に使う事もできます。
基本的には「微分の逆演算」をやるだけですので、微分と別途に「積分の公式」を覚える必要は、それほどない・・とは、思います。一応、頻繁に使うものに関しては色をつけてあります。
微分の公式と比べると、一見簡単な関数の原始関数がやたらと複雑になる場合がある事にも、注意してみてください。
| 対象の関数 | 原始関数(不定積分の計算) | 証明・導出法の概略 |
|---|---|---|
| ①定数(定数関数) | \(\int c dx=cx+C\) | 単項式の1次関数の微分より |
| ②-1 単項式\(x^a\)【a≠-1】 | \(\int x^a dx=\frac{x^{a+1}}{a+1}+C\) | 微分公式と係数を消すために分母調整 次に記すように1/xの時だけは注意 |
| ②-2 \(\frac{1}{x}=x^{-1}\) | \(\int\frac{1}{x}dx=\int x^{-1}dx=\ln |x|+C\) | 自然対数関数の微分公式より。 絶対値がつくのは、x<0 の時でもln|x|の微分が1/x になるため |
| ③ e の指数関数\(e^x\) | \(\int e^xdx=e^x+C\) | \(\frac{d}{dx}e^x=e^x\)によります。 |
| ④-1 自然対数関数 | \(\int \ln x dx=x\ln x -x+C\) | 積の微分公式から逆算するか、部分積分により。 |
| ④-2 対数関数系\(\frac{\ln x}{x}\) \(a^x\ln a\)など |
\(\int \frac{\ln x}{x}dx=\frac{1}{2}(\ln x)^2+C\) \(\int a^x\ln a=a^x + C\) |
合成関数の微分公式により、\(\frac{d}{dx}\frac{1}{2}(\ln x)^2=\frac{1}{2}(2\ln x)\frac{1}{x}=\frac{\ln x}{x}\) 後者は指数関数の微分公式より。 |
| ⑤-1 三角関数 (正弦、余弦、正接) |
\(\int \sin xdx=-\cos x+C\) \(\int \cos xdx=\sin x+C\) \(\int \tan xdx=-\ln|\cos x|+C\) |
正弦と余弦の微分公式より。 正接は、合成関数の微分公式より、 \(\frac{d}{dx}(-\ln |\cos x|)=-\frac{(\cos x)^{\prime}}{\cos x}=\frac{\sin x}{\cos x}\) |
| ⑤-2 三角関数 (その他系) |
\(\int \cot xdx=\ln|\sin x|+C\) \(\int \mathrm{cosec}^2 xdx= -\ln|\cot x|+C\) \(\int \sec^2 xdx=\ln|\tan x|+C\) \(\int \sec xdx =\ln|\sec x +\tan x|+C\) |
\(\cot x=\frac{\cos x}{\sin x}\hspace{10pt}\sec x=\frac{1}{\cos x}\) \(\mathrm{cosec}x=\frac{1}{\sin x}\) 微分により「分母」を作るために、対数関数を利用しています。 |
| ⑤-3 三角関数 (合成関数) \(\sin (nx),\hspace{10pt}\sin^2x\)等 |
\(\int \sin (nx)dx=-\frac{1}{n}\cos (nx)+C\) \(\int \sin^2 xdx=\frac{2x-\sin (2x)}{4}+C\) \(\int \sin x\cos xdx=\frac{-\cos(2x)}{4}+C\) |
sin(nx)は合成関数の微分、 \(\sin^2x\)は加法定理でcos(2x)の形に直して考えます。 |
| ⑥ \(\frac{1}{\sqrt{1-x^2}}系\) (結果に逆三角関数が現れる事があるタイプ) |
\(\int \frac{1}{1+x^2}dx=\arctan x+C\) |x|<1の時、 \(\int \frac{1}{\sqrt{1-x^2}}dx=\arcsin x+C\) |x|>1の時、 \(\int \frac{1}{\sqrt{x^2-1}}dx=\ln |x+\sqrt{x^2-1}| +C\) \(\int \frac{1}{\sqrt{1+x^2}}dx=\ln |x+\sqrt{x^2+1}| +C\) |
逆正接と逆正弦関数については、微分公式から。 残りのものは、合成関数の微分を丁寧に適用すると確かに原始関数となります。 |
| ⑦ \(\sqrt{1-x^2}系\) | \(\int \sqrt{1+x^2}dx\) \( =\frac{x\sqrt{1+x^2}+\ln |x+\sqrt{1+x^2}|}{2}+C\) |x|<1の時、 \(\int \sqrt{1-x^2}dx\) \(=\frac{x\sqrt{1-x^2}+\arcsin x}{2}+C\) |x|>1の時、 |
とても面倒くさい(でも一応表せる)・・という事だけ分かればいいと思います。 もちろん、関数を微分する事で確かに原始関数である事を確かめる事ができます。 |
| 部分積分 | \({\large\int f^{\prime}g dx=fg-\int fg^{\prime}dx}\) | 定積分の公式としても上記に記してあります。 証明は、積の微分公式から。詳細 |
定積分に関する公式の証明
微積分学の基本定理、置換積分の公式、部分積分の公式についての証明をここでは述べます。
(証明)微積分学の基本定理
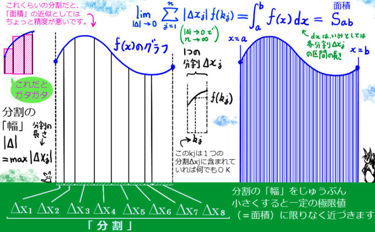
閉区間 [a,x] 上の変数を含んだ形の定積分\(\int_a^xf(t) dt\) を x の関数 S(x) として考え、和の形の定義で表したものについて、微分の定義を当てはめます。
[x,x+h]の閉区間の長さは h で、これをゼロに近づける時は[x,x+h]の分割はこの区間自体だけでじゅうぶんである事に注意すると、
$$\lim_{h \to 0}\frac{S(x+h)-S(x)}{h}=\lim_{h \to 0}\frac{S(x)+S(h)-S(x)}{h}=\lim_{h \to 0}\frac{S(h)}{h}=\lim_{h \to 0}\frac{hf(k)}{h}=\lim_{h \to 0} f(k)=f(x)$$
【最後の所は、x < k < x+h なので、\(\lim_{h \to 0}k=x\)】(証明終)
(証明)置換積分の公式
x=x(u),f(x)=f(x(u)) だとします。【例えば x = sin u, f(u)=\(\sin^2u=x^2\)】
x についての積分区間 [a,b] に対応する u についての積分区間は [p,q] であるとし,
a = x(p), b = x(q)であるとします。
$$F(x)=\int_a^x f(t)dt=\int_{x(p)}^{x(u)} f(g(s))ds$$
$$合成関数の微分により、\frac{d}{du}F(x(u))=\frac{F(x)}{dx}\frac{dx(u)}{du}=f(x)\frac{dx(u)}{du}【∵F(x) は f(x) の原始関数】$$
・・ということは、変数 u に関して F(x) は\(f(x)\frac{dx(u)}{du}=f(x(u))\frac{dx(u)}{du}\)の原始関数のひとつなので、
(※ F(x(u)) を u で微分したら \(f(x(u))\frac{dx(u)}{du}\) になったわけですから。)
$$\int_p^q f(x(u))\frac{dx(u)}{du}du=\left[F(x(u))\right]_p^q=F(x(q))-F(x(p))=F(b)-F(a)=F(b)=\int_a^b f(x)dx $$
(証明終)
【※\(F(b)=\int_a^b f(t)dt,\hspace{10pt}F(a)=\int_a^a f(t)dt=0\)に注意】
(証明)部分積分の公式
積の形の関数に対する微分公式より、
$$(fg)^{\prime}=f^{\prime}g+fg^{\prime} \Leftrightarrow f^{\prime}g=(fg)^{\prime}-fg^{\prime}$$
ということは、f'(x)g(x) の形の関数の不定積分と定積分は
$$不定積分:\int f^{\prime}g dx=\int (fg)^{\prime} dx-\int fg^{\prime}dx=fg-\int fg^{\prime}dx$$
$$定積分:\int_a^b f^{\prime}g dx=\int_a^b (fg)^{\prime}dx-\int_a^b fg^{\prime}dx=[fg]_a^b – \int_a^b fg^{\prime}dx (証明終)$$
※部分積分の証明に関する注:
- 不定積分のほうについては、右辺に不定積分が残る形なので、任意定数 C は残った不定積分に含めると考えて書いていないわけです。
- 上記の微積分学の基本定理と原始関数の箇所でも触れていますが、
\(\int F^{\prime}(x)dx=F(x) + C\) が成立します。
参考:特殊な定積分について
「微分と積分は逆演算」という観点からは計算しにくい定積分の例をいくつか参考として、ここでも挙げておきます。原始関数が初等関数の形で簡単に計算できないものは、じつは多いのです。
そのような場合、定積分を主に面積的に捉えてコンピューターによる「数値計算」を行う事は有用な手段の一つですが、積分区間を「無限大」にする時(そのような種類の積分を「広義積分」と言います)には、敢えて重積分や複素積分を考える事により定積分(の極限値)が簡単な値として導出できる場合があります。そのような例の中には、物理の理論で用いられるものもあります。
- \({\large\int_{-\infty}^{+\infty} e^{-a^2x^2} dx=\frac{\sqrt{\pi}}{a}} \)
証明には敢えて「重積分を使用」します。量子力学などでたまに使う積分です。 - \({\large\int_{-\infty}^{+\infty} e^{-a^2x^2+bx} dx=\frac{\sqrt{\pi}}{a}e^{\frac{b^2}{4a^2}} }\)
同じく、量子力学で使う事がある系の積分です。 - \({\large\int_0^{+\infty}\frac{\sin x}{x} dx=\frac{\pi}{2}}\)
こちらは、敢えて「複素積分」を考える事で、実数範囲の積分(の極限値)が計算できるという例です。この手のものは、結構多くあります。 - \({\large\int_0^{+\infty} \frac{1}{1+x^4} dx=\frac{\pi}{2\sqrt{2}}}\)
これも、敢えて複素関数の範囲で考えるとうまく行く例です。
このページでは述べていない公式や、まだしていない考察も大学数学の微積分学には多く含まれます。このページで述べている基本事項をもとにして、ぜひそれらについても探求してみましょう。必要があれば、このページにも戻ってきてみてください。
参考文献 ・学習に役立つサイトなど
微積分の基本的な公式につきましては高校の教科書などにももちろん載っていますし、大学の微積分の教科書にも載っています。また、多くの外部サイトでも微積分の基本を述べているものは多いので、必要に応じて参照していただければよいと思います。