「マイナスとマイナスをかけるとプラスになる」事の理由と意味について説明します。
(この記事内では「証明」と言わずに「説明」という語を使っています。)
負の数を含む掛け算(積、乗法)の符号の決まり方は次の通りです。
- (+1)×(-1)=-1
- (-1)×(+1)=-1
- (-1)×(-1)=+1
尚、正の数同士の掛け算はもちろん(+1)×(+1)=+1 です。
簡単な引き算による説明
マイナス2かけるマイナス2は、プラス4になります。
これはなぜかというと、「『そのようになるように』計算を定義しているから」なのですが、
なぜそのように定義しているのかを考えてみましょう。
2つの数の引き算を考えます。
5ひく3は、2です。
5-3=2という、小学校で教わるか、あるいは教わらなくても説明されればすぐに分かる計算ですね。
ここで、3という数を2プラス1と考えて、
5から「2プラス1」を引いても、もちろん2という同じ計算結果になります。
■ 5-(2+1)=2
-(2+1)の部分は(-1)×(2+1)=-2-1=-3
文字式であれば -(A+B)= -A-B の計算です。
では、3という数を「4マイナス1」と考えた場合はどうなるでしょう。
その時には
5-3=5-(4-1)と考える事ができます。
ここで-(4-1)の部分を、-(2+1)と同じ計算の仕方で「展開」するとすると、
-(4-1)=(-1)×(4-1)
=-4+(-1)×(-1)という「負の数同士の掛け算」が現れるわけです。

じつは、5から「4マイナス1」を引くという計算をした時に、
「5ひく3」と同じ結果を得るために必要なのが、「マイナス同士をかけるとプラスになる」という計算の定義です。
5から4を引いたら1ですから、5から3を引いた場合よりも「1だけ多く引き過ぎ」なのです。正しい計算結果に補正するために、5から4を引いて1を加えると、5引く3と同じ結果です。
この補正のために加えている分が、マイナス同士のかけ算でプラスになる部分です。
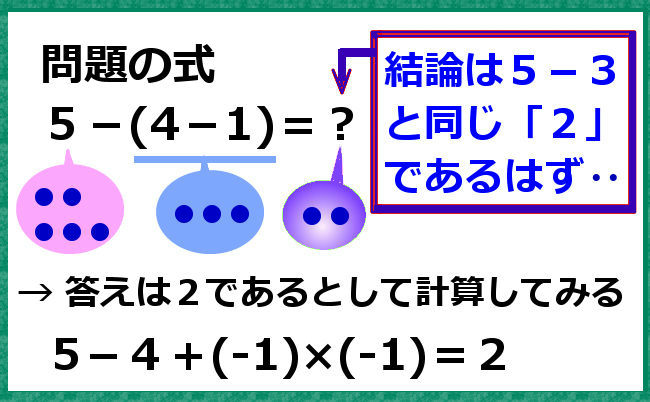
★ 5-3=2ですから、5-3=5-(4-1)=2です。
ここで、負の数を含んだカッコ内を上記の考えで『展開』できるとすると、
5-(4-1)= 5-4+(-1)×(-1)=1+ (-1)×(-1) ですから、
1+(-1)×(-1) =2 ⇔(-1)×(-1) =1 となるわけです。
別の例でやってみると、
例えば6-2=4
6-(4-2)=4
2+(-1)×(-2)=4
(-1)×(-2)=+2
のようになります。
あるいは、次のような図で考えてみる事もできるでしょう。
考え方は1つではありません。
例として7-(5-2)の計算を考える時、仮に7から5を引いたら結果は2ですが、これはもちろん7-3と比較したら「引き過ぎ」ですね。では、多く引き過ぎている部分はどこかというと、マイナス3に対して、「マイナス2が余分」であるわけです。
したがって、7-5は7-3に対して「2を多く引き過ぎている」のですから、「2を加えてあげれば」、7-3と同じ結果になるわけです。式で書くなら、7-5+2=7-3で、左辺が意味するものは「7-(5-2)」であるという解釈もできるでしょう。これはつまり、「-(5-2)=-5+2と考えるべきである」、すなわち、マイナスとマイナスの掛け算はプラスになるべきという説明になります。
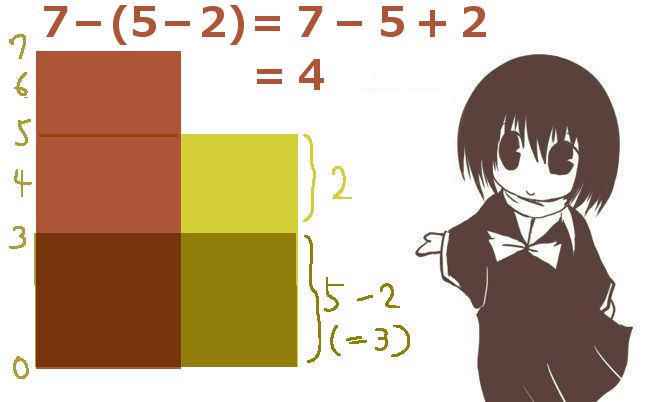
★ A-(A-B)=B ⇔ A-A+(-1)×(-1)×B=B
⇔ (-1)×(-1)×B=B ⇔ (-1)×(-1)=+1 のように考える事もできます。
これは、全体Aから何かを引いたらBになる時、その「何か」とは当然「AーB」であるという考え方ですね。
具体的には例えば7-(7-5)=5といった「当然の計算結果」です。
物理から考えてみる説明
高校数学等で学ぶベクトルは、マイナス符号をつけると(つまりマイナス1を掛け算すると)「逆向き」になるという規則があります。
では、もし「逆向きのさらに逆向き」を考えるとどうなるでしょうか?
それはもちろん、もとの向きに戻るのです。
ですから、その事が「マイナスとマイナスを掛けるとプラスになる」という計算規則と調和するのです。
このように負の数の乗法は物理などでの応用でも意味を持っています。
その考え方のもとでは、マイナス同士の掛け算は次のように説明する事もできます。
まず、1+(-1)=0です。
次に、この両辺に「-(-1)」を加えると考えましょう。
(あるいは両辺から「-1」を引く)
すると、
1+(-1)-(-1)=-(-1)で、
(-1)-(-1)=0と考えるなら、
1=-(-1)
このようにして、「マイナス1にマイナス符号をつけるとプラス1である」と説明する事もできます。
ベクトルで書くなら次のような形です。
$$-(-\overrightarrow{a})=\overrightarrow{a}$$
一般的に物理や工学では、マイナスの符号は「逆向き」の意味で使われます。
マイナス1をかける事によって、速度、力、電流などの向きが、特定の方向とは逆向きである事が表現されるのです。
※この場合には基本的に数学的な考え方が最初にあって物理に当てはめていると考える事ができます。しかし、もし物理法則を説明するために既存の数学体系では不足するものがあった場合には、必要な数学的規則を新たに考えてもよいとも言えます。それは滅多に無い事ではありますが、強調されてよい事であるとも思われます。
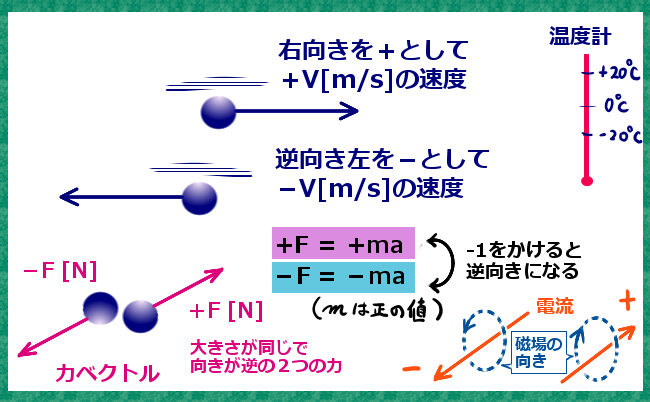
電流の場合。電子の流れと考えてもよいですが、発生する磁場の向きによって電流の向きを考える事もできます。
これらの応用でマイナス符号を使う時も、マイナス同士の掛け算はプラスになるという計算規則をそのまま使う事ができます。
あるいは、温度計などで、冬場に「気温はマイナス3度」といった表現は聞いた事があると思います。そのように、基準点であるゼロを突き抜けて下がる量がある時にもマイナスの考え方は便利です。ただしこのような使い方の場合はマイナスの「掛け算」はあまり使いませんね。用途や使用目的に応じて特定の計算を使うか使わないかは変わってきます。
デジタルでの使い方
デジタルで絵を描いたり、ゲームを作ったりという時にもプログラムのレベルにおいて(-1)×(-1)の演算が使われる事があります。一般的なプログラミング言語では乗法の演算として(-1)×(-1)=+1という通常の数学での実数の演算と同じ規則が採用されています。【多くの場合、プログラミングでは乗法の演算の記号としては *(アスタリスク)が使われます。】
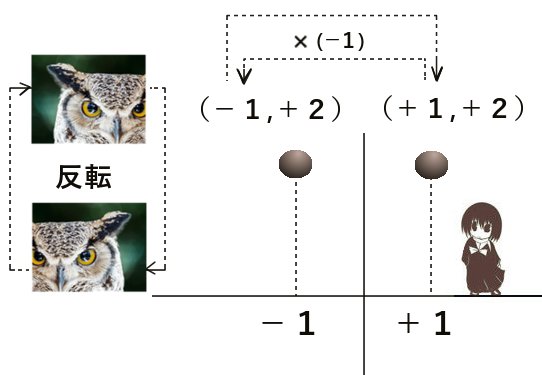
普通、デジタルで画像を画面に表示させる時には座標の指定が行われています。この時に画像の表示位置や画像の倍率指定においてマイナス符号を「反転」の意味を表すように紐づける事が可能で、さらに負の数同士の乗法も上手に活用する事ができます。
例えば倍率に対しては(-1)を1回乗じると向きの反転が行われ、もう一度(-1)を乗じると元の向きに戻るという演算として使えるわけです。+1を乗じた時には数値が変化しない事から、「何も変化なし」を意味します。
座標の反転に関しては、x座標だけでなくy座標も同時に符号を反転させれば「原点に対して対称」である位置への移動を考える事ができます。
倍率の指定での使い方に関しては、例えば「-2」を乗じる事で「反転して2倍に拡大する」といったように反転と大きさの倍率を統一的に扱う事ができます。
市販されているソフトウェアを使う時には数学的な演算を自分でやらなくてもよい(やらなくてもよいように設計されている)事は多いですが、自分でもプログラミングをやる場合は知っておくと便利です。また、自分ではプログラミングをやらなくても教養的な知識として知っておいてもよい事ではないかと思います。
考え方としてはベクトルに対しての応用と全く同じで、(-1)×(-1)=+1を上手に使っているわけです。
より数学的な考察と数学教育上の問題
最初の例のように
5-(4-1)=5-4+(-1) × (-1) という計算が
5-(4-1)=3に等しいと考える説明は、
もう少し詳しい数学の用語で言うと「分配則(あるいは分配法則)が成立する」という条件での説明を述べています。分配則は式の展開のような計算規則を指します。
ち a(b+c) = ab + ac が成立するというのが分配則の内容です。それが負の数に対しても成立すると考える(そのような集合を考える)事によって負の数同士の乗法も考える事になります。
言い換えると、もし「負の数に対する分配則」を認めない(認めない集合を考える)のであればその時点で「負の数同士の乗法」に対して理由の説明も証明も何も無い事になるとも言えるわけです。
これは前述の具体例での説明での7-(5-3)のような計算で「マイナスの数についても式の展開を考えるなら」という点を強調している理由でもあります。
もしもその分配側を使った計算自体があり得ないと考えるのであれば、マイナス同士の掛け算という計算自体があり得ないためです。
であるから、もし中学生の人が「マイナスに対して掛け算を考える事自体がそもそもおかしい!認めない」と言うなら、必ずしも誤りとは言えません。考えている対象の数学的集合が異なれば、そういった話の食い違いが生じます。
従って当該反対意見には「それはもっともな事であるが、ここではそのような性質を持つような数学的集合を定義して、考えてみよう」と言うのが正しい回答(「解答」ではありません)かもしれません。
さらに言えば「優先して学ぶべき数学的対象は何か」という意味ではさらに説明が必要となるとも言えます。
同じ「計算を多く行う」学問でも例えば商学(簿記や会計などを扱う学問)であれば負の数同士の乗法や除法はあまり重要ではないし、それ以前に実数に対する深い考察自体がそれほど重要ではないと言えます。
しかし対象の学問が理学・工学系であると話が変わってくるわけです。
純粋数学の研究を特に行うわけではない中学や高校の授業や講義では、やはり「数学はどのように使われるのか」という事まで含めて考えるべきなのかもしれません。負の数を考えなくてもよい場面もあるし、前述のように逆に考えたほうがよい場面も存在するからです。その事まで含めて説明をする必要がある可能性は大いにあるのではないでしょうか。
負の数同士の乗法で非常に特徴的な利点としては何かの向きを変えた時に、さらにもう一度向きを反転させると「もとの向きに戻る」という事の表現に使える事であると言えます。
これは数学の応用という観点からだけでなく、純粋数学的に数学の考察をしていくうえでももちろん重要な事項となります。例えば三角関数の微分を繰り返すともとの関数に戻りますが、これは(-1)×(-1)=+1の演算がなければ成立しません。当該演算は、微積分も含めて実数や複素数とその関数を数学的に調べていくうえでも重要な基礎となっている関係式であると言えます。

■動画の声優御担当:ステ♪ 様 http://sute.tabigeinin.com/
BGM:音楽の卵
