図形・平面幾何 | 理数系学習サイト　kori

三角形の角の二等分線

恭平

三角形の角を二等分する線を引いた時に成立する１つの図形的性質があります。

これは高校入試の図形問題でよく出題され、場合によっては大学入試で部分的に扱われる事もあります。

三角形の角の二等分線に関して成立する関係

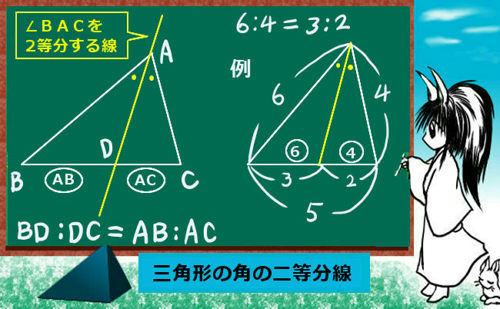
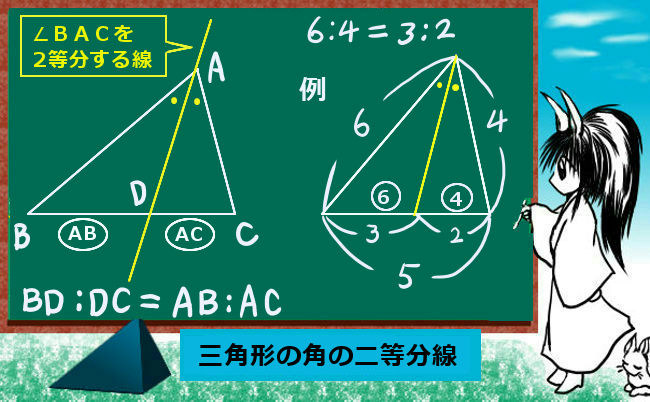
△ＡＢＣにおいて線分ＢＣ上に点Ｄがあり、線分ＡＤは∠ＢＡＣを２等分するという。
（つまり∠ＢＡＤ＝∠ＣＡＤとなっている。）
この時、線分の長さの比についてＡＢ：ＡＣ＝ＢＤ：ＣＤが成立する。

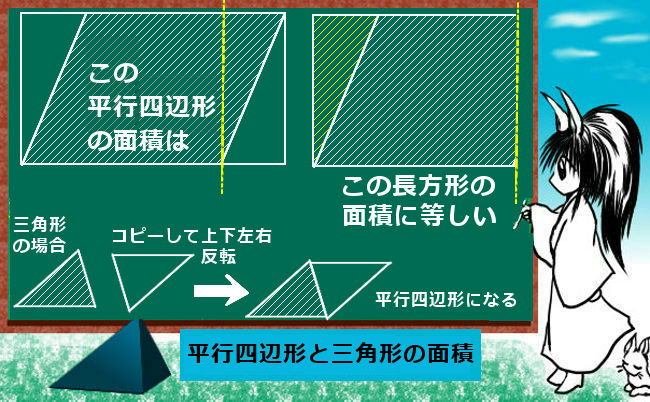
まず、三角形の１つの角を二等分する線を引きます。これは、例えば６０°の角度であれば３０°と３０°に分割する線を引くという意味です。

次に、その線が１つの辺とぶつかる交点を考えます。すると、じつはその交点は、他の２辺の長さの「比」でその辺を分割しているのです。こういったものは、図で見たほうが多分分かりやすいでしょう。

三角形の二等分線① — 例えばＡＢ＝６、ＡＣ＝４であれば点ＤはＢＣを６：４＝３：２で分割します。ＢＣ＝５であればＢＤ＝３、ＤＣ＝２であると決まるという事です。

これを証明するのは比較的簡単です。次のようにします。
（★ただし、入試の問題を解くという観点からは結果の関係式を確実に覚えておいたほうがよいです。しかし仮に忘れた時でも証明は難しくないという事です。）

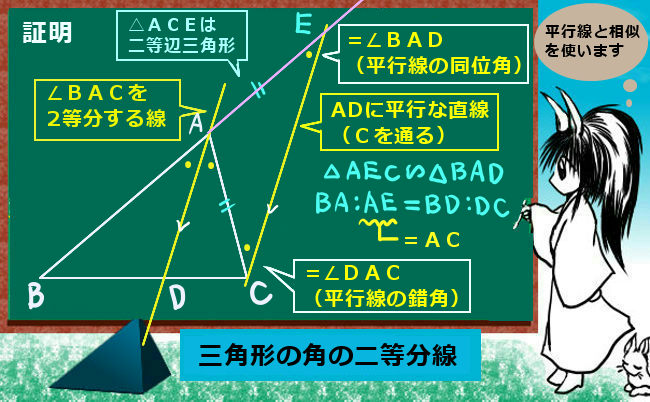
まず、二等分する角につながる三角形の辺の１つを延長します。次に、二等分する角の対辺の１端から、角の二等分線に「平行」な直線を引きます。すると三角の相似関係により証明ができるというのが簡単な流れです。この時、二等辺三角形ができる事に気付く事も１つの重要な点です。

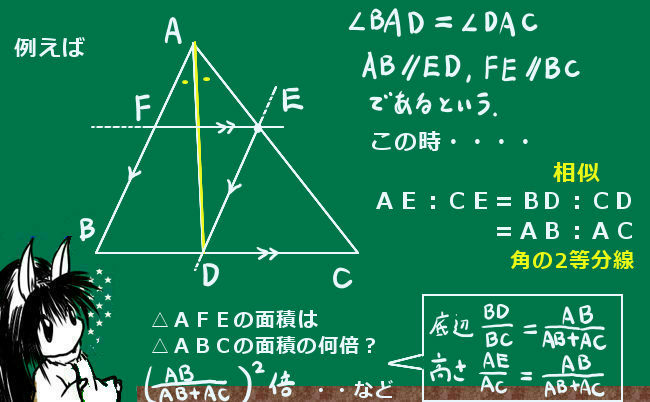
三角形の二等分線②（証明） — １つの辺の延長と、補助線として設ける平行線をつなげると大きな１つの三角形ができます。それと元の三角形の相似関係を考え、さらに図の△ＡＣＥが二等辺三角形である事に注目すると関係式が得られるのです。

この関係が中学校の数学、特に高校入試で問われる場合は、単独ではなくて他の図形上の関係と合わせて計算をさせる事が多いと思います。例えば、三角形の相似問題の１つの条件として使われたり、三角形の面積比を計算させるといった具合です。

また、円周角関連の事項と合わせた出題もあり得ます。この手の問題は計算を面倒にさせようと思えばいくらでもそのように問いを作れるので、いくらか練習しておかないといきなり問われた時になかなかうまくいかない事もあろうかと思います。

高校入試などでは三角形の面積比を計算させる問いなどで使わせる例があります。この図の例では、例えば情報としてＡＢ、ＡＣ、ＢＣの長さだけが与えられていて△ＡＥＦと△ＡＢＣの面積比を計算させるといった具合です。

さて、この三角形の二等分線に関する問いは多いですが、中学での勉強を終えて高校での学習に移る時、そんなに使うのかというと正直あまり使わないと思います。ただし、図形の平行・直角・相似・合同といった考え方は引き続き使用される事があります。

そのため、試験問題を解くという事を抜きにして語るのであれば、重要なのは関係式が成立する「理由」のところだと思います。平行線の性質や相似関係によってこのような事が言えるという事が、本当は一番覚えて理解しておきたいところかとは思います。

円・扇形に関連する面積の計算

恭平

円と扇形の面積に関連する計算の数学・算数の問題について説明します。

円と扇形

まず、円の面積は半径の２乗と円周率（≒３.１４）の積です。

円の面積

円の面積＝半径×半径×３.１４

例えば、半径が２メートルの円の面積はおおよそ２×２×３.１４＝１２.５６平方メートルという事です。

★尚、「円周率」は「円の周の長さ」と直径の比の事です。なぜ円周率が３.１４なのかは別途に詳しくまとめています。

他方、「扇形」とはピザやアップルパイのように、中心からまっすぐ円周に向かって円を切り取った部分のような形の図形の事です。

この扇形の面積を計算するには、角度を使います。要するに角度が全体の何割かという事で、面積が円全体の何割かという事で計算するわけです。

扇形の面積

$$扇形の面積=円の面積×\frac{扇形の角度}{３６０°}=半径×半径×３.１４×\frac{扇形の角度}{３６０°}$$ 扇形の角度とは、もちろん中心部分の角度の事です。
角度を「弧度法」で表す場合には、弧度法で表した扇形の角度を $2\pi$ で割ります。

例えば、簡単な例では半円は円の半分の面積、１／４円の面積は円の１／４の面積です。６０°の角度の扇形の面積は円の１／６の面積になります。

円と扇形の面積の計算問題① — 弧度法とは角度と対応する円周部分の長さを角度その物として扱う方法です。主に高校数学以上で扱います。面積の記号にはＳ(surface)やＡ(area)をよく使います。

円・扇形に関する面積の応用問題

さて、算数や中学数学での図形の問題で、円や扇形に関連する「変な形」の図形の面積を計算させる問題があります。例えば、四角形から円を切り取った部分の面積や、１／４の円を組み合わせて作ったラグビーボールのような図形の面積です。

基本的には、ある図形の面積から別の図形の面積を差し引き、それをうまく組み合わせて変な形の図形の面積を上手に計算するのです。

例えば、１辺の長さが２Ｒである正方形を考えましょう。これに円が内接する場合、円の半径はＲになります。そこで、正方形から円の部分を切り取った図形（４つ分）の面積は次のようになります。

$$S=(2R)^2-R^2×3.14=(4-3.14)R^2=0.86R^2$$

Ｒ＝１で正方形の１辺が２で正方形の面積が４である場合、約０.８６が切り取られた部分の面積の合計というわけです。１部分の１つだけの面積を問う問題であればそれをさらに４で割ります。

ラグビーボール型の面積については、２段階を踏みます。
今度は円の半径が正方形の１辺に等しいのでこれをＲとしましょう。

まず、正方形から４分円（円の４分の１）を引きます。

そして、その部分の２倍を、正方形から引きます。
これがラグビーボール型の図形の面積になります。

$$S=2×(R^2-R^2×3.14÷４)=2×0.215×R^2=0.43R^2$$

Ｒ＝１であればラグビーボール型の図形の面積は約０.４３という事になります。

この手の問題は図形の組み合わせによっていくらでも複雑にできるところがありますが、基本的にはこのように公式で面積が分かる図形から切り取った図形を組み合わせて計算します。

中学数学の場合は、三角形との組み合わせの問題もあり得ます。例えば、三平方の定理や図形の相似の関係と組み合わせるパターンです。

次図はその１つの例で、隠れてる扇形を見つける必要がある事、三平方の定理か三角比を使って１つの辺の長さを出す必要がある事から、一手間かかるタイプの問いです。

円と扇形の面積の計算問題③ — この問題は小学校の知識だけで解答を出すのは多少難しいパターンです。三角形の辺の長さから扇形の角度を出して、未知の１つの辺の長さも計算する事になります。半円が交わる点がちょうど長方形の中の中間にある事を使います。

高校数学の場合はこのような問いが出題される頻度は少なくなりますが、積分の問題として、似たような図形の面積を計算させる問いは出題されます。

台形の面積公式【算数と図形】

恭平

小学校や中学校で教わる台形の面積を出すための公式というものがありますね。

台形の面積公式

台形の面積＝｛（上底）＋（下底）｝×（高さ）÷２

これくらいなら覚えれるという人も多い一方で、なんでこんな変な公式になるのか疑問に思いながら覚えた人も中にはいるかもしれません。この公式がなぜ成立するのかをこのページでは述べます。理由は全く難しくありません。

台形の面積公式① — まず台形の図を描いてみましょう。四角形のうち、１組の対辺同士が平行であるものを「台形」と呼びます。２組とも平行であればそれは「平行四辺形」です。

台形の面積公式の導出方法はじつにシンプルで、

「台形をコピーして上下左右ひっくり返してぴったり貼り付けると平行四辺形になる」

なんとこれだけです。

まず、もとの台形を上下・左右逆さまにひっくり返したものを用意します。まず上下に反転し、左右にも反転させる事が１つポイントです。

これを、もとの台形の横にくっつけます。

尚、「ぴったり」きれいに必ずくっつくという事は平行線の錯角の関係によって保障されるのです。

すると、平行四辺形の面積は（底辺）×（高さ）であるわけですが、この大きな平行四辺形の「底辺」は、台形の（上底）＋（下底）なのです。下底に、上底だった部分がくっついていますので。

ただ、その平行四辺形の面積は台形２個分の面積です。

そのため、もとの台形の面積はその半分であって、「２で割る」わけです。

台形の面積公式② — 台形を２つ分合わせた平行四辺形の面積を出し、それから半分個にする事でもとの台形の面積であるとする計算が台形の面積公式です。

これで、公式「台形の面積＝｛（上底）＋（下底）｝×（高さ）÷２」が出ます。【証明終り】

尚、三角形の面積公式も三角形２つで平行四辺形を必ず作れる事に由来します。

「２で割る」というのは、じつは台形の場合と同じ理由であるわけです。

また、平行四辺形の面積が（底辺）×（高さ）となる理由は、出っ張っている部分を切り取って反対側につけると「長方形」になるためです。

三角形の面積公式の出し方は、ある意味台形の面積公式の出し方に似ています。いずれにしても、三角形も平行四辺形も長方形に直せるという事が面積公式の根拠であるわけです。三角形の場合、もとの三角形の２個分が平行四辺形なので、最後に２で割るのです。

さらに言うと、長方形の面積は正方形の面積の和に最終的には還元されます。

面積の単位は「平方メートル」ｍ²（あるいは平方センチメートルcｍ²）と書きますね。つまり面積というものは１ｍ²の正方形が何個分あるかという事なのです。もちろん、それを数えるのは大変ですから、面積の公式というものを使うわけです。

台形の面積公式の場合は、言われれば覚えれる人も多いと思います。ただ、たまには、どういう理由でそうなってるのかを考えてみると楽しい事もあるかもしれません。

尚、こういった初歩的な面積計算は、高校や大学での積分の理論の基礎になっています。