この記事では、偏微分について説明します。
★ 英名は、「偏微分」の演算の事を partial differentiation、
偏微分によって得る「偏導関数」を partial derivative と言います。
この偏微分の考え方は、解析学・微分積分学的にも重要ですが、特に物理での応用で重要です。大学の物理学では割と初歩的な理論の中でも偏微分を普通に使いますので、ぜひ知っておきましょう。まずは記号に慣れていただく事が大事かと思います。
合成関数に対して成立する偏微分の公式も、
物理学の種々の分野の要所で用いられる重要公式です。
偏微分の定義と使い方
では、まず偏微分の定義と簡単な計算方法、物理等での基本的な使い方を見てみましょう。「偏『微分』」という名の通り、微分の仲間です。
■ 偏微分の定義 ■ 偏微分の簡単な計算例 ■ 物理での偏微分の使われ方の例
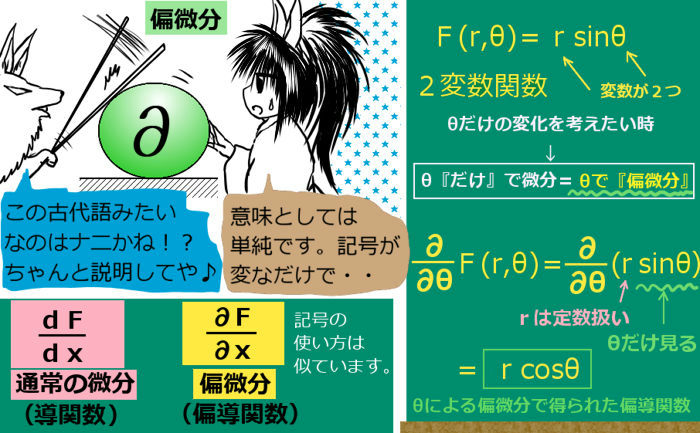
偏微分に対して、通常の微分を「常微分」とも言います。
偏微分の定義
偏微分の定義自体は非常に簡単で、要するに、多変数の関数において、「1つの変数だけに着目し、他の変数は定数とみなして微分の計算をする事」です。
多変数関数F(x,y,z,・・)【てきとうな例:F(x,y,z)= xy + z】に対して、
を1つの変数に着目して、
演算「xでの偏微分」を次のように定義し、偏微分によって新しくできた関数を偏導関数と呼びます。
変数yやzに対しても同じように定義します。
$$ \large \frac{\partial}{\partial x}F(x,y,z,\cdots)=\lim_{h\to 0}\frac{F(x+h,y,z,\cdots)-F(x,y,z,\cdots)}{h}$$
$$記号「\partial」は、「ラウンド・ディー」という名で呼ばれます。$$
通常の微分の時と同じく、偏微分によりできた偏導関数の事を単に「偏微分」と
呼んでしまう事も多くあります。また、∂/∂xなど、基本的には通常の微分と同じく種々の表記方法が認められています。
偏導関数に特定の値を代入した「偏微分係数」は
$$\large \frac{\partial F}{\partial x}(a,b,c)\hspace{5pt}や\hspace{5pt}\partial xF(a,b,c)$$のように書きます。
偏微分の簡単な計算例
例として、てきとうな関数 F(x,y,z)= xy + z をxで偏微分してみましょう。この時、yとzは定数扱いにしてxだけで「微分」すればよいのです。
$$\frac{\partial}{\partial x}F(x,y,z)=\frac{\partial}{\partial x} (xy + z) =y $$
この場合、xy の部分はxでの偏微分ではxの部分だけ微分してyは定数係数扱いです。
z項の部分はxに関しては定数と考えて、
zをxで偏微分すると0になるわけです。(∂/∂x)z=0 という事です。
基本的な考え方は簡単ではないでしょうか?
★ zがxに対する「独立した」変数である場合にこのような計算になります。もし、zがxの関数であったら、後述する合成関数の偏微分公式を使う必要があります。いくつかの変数が互いに「独立」であるか「従属」であるかは、場合によっては結構重要になります。
もう1つ例として、極座標の形で表した関数の偏微分を考えてみます。F(r,θ)=rcos θ とします。これに対するrの偏微分と、θの偏微分を考えてみましょう。
$$ \frac{\partial}{\partial r}F(r,\theta)= \frac{\partial}{\partial r} (r\cos \theta)= \cos \theta $$
$$ \frac{\partial}{\partial \theta}F(r,\theta)= \frac{\partial}{\partial \theta} (r\cos \theta)= -r\sin \theta $$
偏微分のラウンドディーの記号に慣れてないと難しく見えるかもしれませんが、やってる事は通常の微分と計算と同じなので、じつは単純なのです。
物理での偏微分の使われ方の例
物理では、関数が座標成分と時間の両方の関数である場合に、「時間だけの変化率」を考えたい時に時間による偏微分を行います。
例えば電磁誘導は磁場の変化(時間微分)によって起電力が発生するというものですが、
電場は時間以外に位置座標 x, y , z の関数でもあるので「時間変化」という事を明確にするために時間による偏微分で表現します。
$$電磁誘導の式:\mathrm{rot}\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\hspace{10pt} \overrightarrow{E} :電場 \overrightarrow{B}:磁場【あるいは磁束密度】 $$
時間ではなくて位置座標による変化という事を明確にするのであれば、位置座標による偏微分を考えます。
例えば、磁場に関しては次の式が必ず成立します。 「単独で存在する磁荷」は無い事を表現します。
$$ \large \frac{ \partial B_X}{\partial x}+ \frac{ \partial B_Y}{\partial y} + \frac{ \partial B_Z}{\partial z} =0 \hspace{10pt} \overrightarrow{B}=(B_X,B_Y,B_Z) $$
このように、意味としては「どの変数に着目してるのか?」それを明示しているのが偏微分というものです。使われ方としては、基本的には単純なのです。
(※微分方程式の解き方も含めて、計算は面倒になる場合も確かにありますが、偏微分そのものが複雑な演算というわけではないという事です。)
工学の場合は、分野によってはそれほど偏微分の理論を使わずに通常の微分で大体足りるものも中にはありますが、物理では力学などの基礎的な部分も含めて、偏微分の考え方は非常に多く用います。
重要公式:合成関数に対する偏微分
合成関数を考える場合、じつは合成関数に対する偏微分の公式は、通常の1変数の時の合成関数の微分公式と形が異なります。この点を誤解すると物理などの理論で混乱を招くので、公式の形が変わるという点は偏微分の基礎理論の重要ポイントの1つです。
■ 多変数関数の合成関数の考え方 ■ 合成関数に対する偏微分の公式 ■ 公式の証明

偏微分の時の形の特別な場合が常微分の場合の合成関数に対する微分公式であるとも言えます。
多変数関数の合成関数の考え方
1変数の場合、例えば F(x) に対して x = G(t) であれば F(G(t)) という合成関数になります。
これに対して、多変数の場合は、例えば F(x,y) について、xとyのそれぞれについて、別の多変数 u, v を用いて x = X(u, v) , y = Y(u, v) で表し、
F(x,y) = F( X(u, v) , Y(u, v) ) となるという考え方をします。これは、慣れないと少し分かりにくいかもしれません。
考え方としては、3変数を2変数による合成関数として考えたり、2変数を3変数による合成関数と考える事もできます。
これは、例えば位置座標 x, y, z で表される関数を3次元の極座標で表すために r, θ, φ という別の3つの変数を用いた合成関数として表す事が可能です。(計算は、一般的に結構面倒くさくなります。)
合成関数に対する偏微分の公式
公式は、次の通りです。変数を1つだけと考えると、通常の合成関数の微分公式になります。
多変数関数F(x,y,z,・・)に対して、x, y, z, ・・・のそれぞれが u, v, w, ・・の多変数関数である時、
つまり x = X(u,v,w,・・), y = Y(u,v,w,・・), z = Z(u,v,w,・・),・・の時、
F(x,y,z,・・) に対して u, v, w, ・・のそれぞれで偏微分して得る偏導関数は次のようになります:
$$\frac{\partial}{\partial u}F(x,y,z,\cdots)=\frac{\partial F}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial F}{\partial z}\frac{\partial z}{\partial u}+\cdots$$
$$\frac{\partial}{\partial v}F(x,y,z,\cdots)=\frac{\partial F}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial F}{\partial z}\frac{\partial z}{\partial v}+\cdots$$
$$\frac{\partial}{\partial w}F(x,y,z,\cdots)=\frac{\partial F}{\partial x}\frac{\partial x}{\partial w}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial w}+\frac{\partial F}{\partial z}\frac{\partial z}{\partial w}+\cdots$$
$$\cdots$$
$$★これらの式において、\frac{\partial F}{\partial x}\frac{\partial x}{\partial u}は、2つの偏導関数の掛け算です。$$
u, v, w, ・・のそれぞれでの偏微分について、このような和の形になります。
何変数でも同じ事ですが、例えば2変数に対して2変数による合成関数を考える時、つまり F(x,y) に対して x = X(u,v), y = Y(u,v) の時に、F に対して u, v で偏微分する時は次のようになります。
$$\frac{\partial}{\partial u}F(x,y)=\frac{\partial F}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial u}$$
$$\frac{\partial}{\partial v}F(x,y)=\frac{\partial F}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial v}$$
1変数に対して別の1変数の合成関数であれば、次のように、通常の1変数の合成関数の公式と一致します。
$$1変数の場合は \frac{\partial}{\partial t}F(x)= \frac{\partial F}{\partial x}\frac{\partial x}{\partial t}=\frac{dF}{dx} \frac{dx}{dt} $$
公式の証明
合成関数に対して偏微分を考える場合、なぜ和が出てくるのか?という話ですね。基本的の証明の方法は、1変数の場合の、積や商の微分公式の証明と似ています。プラスとマイナスがゼロになって「隠れている」項があるわけです。
証明は、偏微分の定義の式に戻って計算を進めます。1つの変数 u で偏微分する時は、v, w,・・等は計算に影響しないので、ここでの証明では v, w 等の記載を省かせていただきます。本質的には、それらの変数もあると思ってください。
$$F(X(u+h),Y(u+h),Z(u+h))-F(X(u),Y(u),Z(u))に対して、$$
$$F(X(u),Y(u+h),Z(u+h))- F(X(u),Y(u+h),Z(u+h)) および$$
$$F(X(u),Y(u),Z(u+h))- F(X(u),Y(u),Z(u+h)) を加えます。 $$
すると、Fに対する u の偏導関数は次の和の形になります。
途中で平均値の定理を用いていて、xに対して特定の値を代入している部分があります。
$$ \large \frac{\partial}{\partial u}F(x,y,z) $$
$$= \large \lim_{h\to 0}\frac{F(X(u+h),Y(u+h),Z(u+h))-F(X(u,v),Y(u,v),Z(u,v))}{h} $$
$$ \large =\lim_{h\to 0} \frac{F(X(u+h),Y(u+h),Z(u+h))- F(X(u),Y(u+h),Z(u+h))}{h} $$
$$ \large + \lim_{h\to 0} \frac {F(X(u),Y(u+h),Z(u+h))- F(X(u),Y(u),Z(u+h))}{h} $$
$$ \large + \lim_{h\to 0} \frac{F(X(u),Y(u),Z(u+h))- F(X(u),Y(u),Z(u))}{h} $$
$$ \large =\lim_{h\to 0} \frac {\{X(u+h)-X(u)\} \partial x F(\phi_X,Y(u+h),Z(u+h))}{h} 【平均値の定理】$$
$$ \large +\lim_{h\to 0} \frac {\{Y(u+h)-Y(u)\}\partial y F(X(u),\phi_Y,Z(u+h))}{h}$$
$$ \large +\lim_{h\to 0} \frac {\{Z(u+h)-Z(u)\} \partial z F(X(u),Y(u), \phi_Z) }{h}$$
$$ \large =\lim_{h\to 0} \left\{\frac {X(u+h)-X(u)}{h} \partial x F(\phi_X,Y(u+h),Z(u+h))\right\} $$
$$ \large +\lim_{h\to 0} \left\{\frac {Y(u+h)-Y(u)}{h} \partial x F(X(u),\phi_Y,Z(u+h))\right\} $$
$$ \large +\lim_{h\to 0} \left\{\frac {Z(u+h)-Z(u)}{h} \partial x F(X(u),Y(u),\phi_Z)\right\} $$
$$ \large = \frac{\partial x}{\partial u} \frac{\partial F}{\partial x} + \frac{\partial y}{\partial u} \frac{\partial F}{\partial y} + \frac{\partial z}{\partial u} \frac{\partial F}{\partial z}= \frac{\partial F}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial u} + \frac{\partial F}{\partial z}\frac{\partial z}{\partial u} 【証明終り】$$
一番最後のところは掛け算の順番を入れ替えて書き直しただけです。
$$ \large \partial x F(\phi_x,Y(u+h),Z(u+h))などは、y=Y(u+h),z=Z(u+h)に値を固定して$$ $$ \large xで偏微分し、x=\phi_x を代入したものです。\phi_x \in [X(u),X(u+h)]$$ $$ \large また、\lim_{h\to 0}\phi_X =X(u) であり、\phi_Y,\phi_Zについても同様です。$$ ここではX(u,v,w,・・)を略記してX(u)と書いているので、 $$ \large \lim_{h\to 0}\frac {X(u+h)-X(u)}{h} の部分は偏微分 \frac{\partial X(u,v,w,,\cdots)}{\partial u} =\frac{\partial x}{\partial u} です。$$ 平均値の定理は使用しなくても別にいいのですが、hの処理を見やすくするために使用しました。
1変数の場合は上記のようにプラスマイナス0を利用した項の付け加えが必要なかったので、和の形ではなく1項だけになります。
★ x,y,z,・・の側の変数がn個の場合も、同様の形のn個の和として表せます。
例として、4変数の場合を考えてみましょう。つまり、F(x,y,z,t) に対して、x,y,z,s が u, v,・・・の関数である場合です。
この場合、次のものを加えて定義の極限を考えればいいのです。
$$F(X(u),Y(u+h),Z(u+h),T(u+h))- F(X(u),Y(u+h),Z(u+h),T(u+h)) $$
$$+F(X(u),Y(u),Z(u+h),T(u+h))- F(X(u),Y(u),Z(u+h),T(u+h))$$
$$+F(X(u),Y(u),Z(u),T(u+h))- F(X(u),Y(u),Z(u),T(u+h))$$
このような感じで、u と u+h の組について、1つずつずらしていく形で組み合わせれば、何変数であっても上記の証明と同じ手順で合成関数に対する偏微分の公式を証明できます。

合成関数の偏微分は物理の中では様々な箇所で用いられますが、例えば全微分というものとの関連で熱力学や流体力学の理論で用いたり、リーマン幾何学との関連で相対論で計算を考える時もあります。また、基本分野の古典力学の理論でも使用する事があります。得られた結果は電磁気学等でも使用します。
★ 関連記事:偏微分の応用の例:位置エネルギーと保存力の関係
