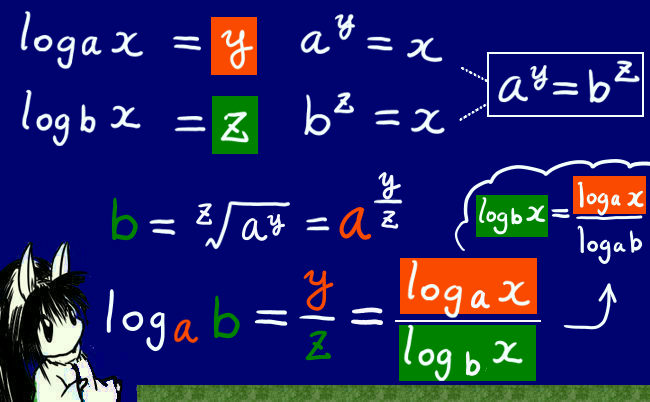対数【たいすう】関数 y= logax について説明します。
関数ではなく、何か1つの値logabについて考えた時は単に「対数」と呼びます。
英:対数関数・・logarithmic function
対数・・logarithm【「比」と「数」を意味するギリシャ語から作った造語と言われる】
定義と表記
対数関数とは、ある正の数aを「何乗したら」xになるのかを、xの関数として表したものです。
logaxと表記し、対数関数と呼びます。これは、指数関数の逆関数になります。
指数関数の逆関数、すなわち「ある正の数a【≠1】をy乗したらxになる」という意味になる関数を
対数関数と言い、y=logaxと書きます。
$$a>0\hspace{3pt}かつ\hspace{3pt}a≠1のもとで$$
$$\large{x=a^y\Leftrightarrow y=\log _a x}$$
この時、1でない正の数aの事を「底」【てい】と言います。
y=logax の定義域はx>0です。
特定の数bに対する対数 logabを考える時には「aを底としてbの対数を取る」という表現をする事があります。また、logabにおけるbを「真数」【しんすう】と呼ぶ事もあります。
例として「10という数を何乗したらxになるか」を考えた時、
その値が 「10を底とする対数関数」であり、log10xと書きます。10が対数関数の底【てい】です。

数学の応用や、理論の多くの場合でも「底」として使われる数は大体決まっている事が多く、
それは10とe(≒2.718・・) と2です。
(もちろん必要があれば他の値を底として考える事ができます。)
これらのうち、10を底とする対数を常用対数 (common logarithm)と言い、
log10xを略記して logxと書く事があります。桁数がやたらと大きい場合に使われる事が多いようです。
また、eを底とする対数を自然対数(natural logarithm)と言い、
logexを略記して lnxと書く事があります。(「ログ・ナチュラル」と読む事があります。)
これはeの指数関数とともに微積分の理論で重要です。
他方、情報理論などでは2を底とする対数を使う事があります。
これは、0と1の2進数を扱う事と関連があります。
logxという略表記はじつは意味が一貫してないところがあり、常用対数を表す事が多いのですが、人によって自然対数を表したり、2を底とする対数として表す事もあります。
そのため「以下、log10x= logxと表記する」といったように、普通は断り書きをつけて使われます。
logax の底aは「正の数」で「1ではない」値を考えるというルールがあります。
もし底が1の場合には、1を何乗しても1になってしまうためで、0の場合も同様です。
またもし底が負の数の場合を考えると、ところどころで「穴」が生じます。
例えば-2の2乗は4ですが、3乗すると-8になります。
という事は実数の範囲で考えれば(-2)y=8になるyは存在しないという事になり、関数として見た時にx=8のところが存在しない事になってしまいます。
そのため、負の数のxが取り得る範囲からは除外するという考え方をします。
少しややこしいですが、次に具体例でも示すように対数関数自体の値は0や負の数もとり得ます。y=logaxについてx>0で、yは実数全域の値をとり得るという事です。
y=logaxの、a, x, y のとり得る値の範囲を整理すると次のようになります。
- a:特定の数で、1以外の正の実数。a>0かつa≠1
- x:変数で、0より大きい数。x>0
- y:対数関数の値。範囲は実数全域。0や負の数も含め、任意の実数であり得る。
具体例とグラフ
2を底とした時、
x=2は「2の1乗」
x=4は「2の2乗」x=8は「2の3乗」
x=1は「2の0乗」
x=1/2は「2の『-1乗』」
x=1/4は「2の『-2乗』」
これら「○乗」の部分が対数関数の値となり、log2xの表記で書くと次のようになります。
log22=1
log24=2
log28=3
log21=0
log2(1/2)=log2(2-1)=-1
log2(1/4)=log2(2-2)=-2
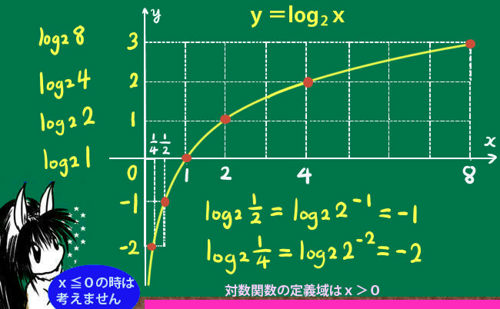
点を座標上にプロットしてy=log2xのグラフを描くと次のようになります。
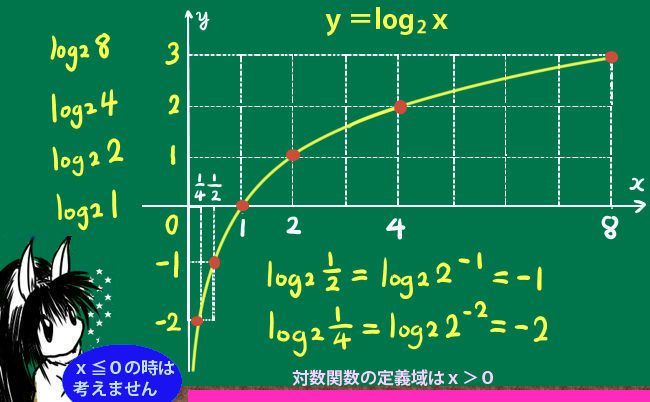
この時、2は正の数ですから、x=0やx=-1のような場合、2を何乗してもそれらの値にならないので、x≦0については考えない・・対数関数の定義域から除外するという考え方をします。
10を底にして考えた時は
x=10は「10の1乗」
x=100は「10の2乗」
x=1000は「10の3乗」
x=1は「10の0乗」
x=0.1(=1/10)は「10の『-1乗』」
x=0.01(=1/100)は「10の『-2乗』」
x=\(\sqrt{10}\)(≒3.162)は「10の『1/2乗』」
これらを log10xの表記を使って書くと、次のように表現できます。
log1010=1
log10100=2
log101000=3
log1010000=4
log101=0
log100.1=-1
log100.01=-2
log10\(\sqrt{10}\)=1/2
基本公式
対数関数に関して成立する基本公式には次のようなものがあります。
- logax+logaz=loga(xz)
- loga(1/x)=-logax
- logax-logaz=loga(x/z)
- logaxb=blogax
- 底の変換公式:$$\log _bx=\frac{\log \large{_a}x}{\log \large{_a}b}$$
①対数の和に関する公式:
au=x, aw=zとすると、xz=auaw=au+wなので、loga(xz)=u+wで、
au=x ⇔ logax=u, aw=z ⇔ logaz=w なので
loga(xz)=u+w=logax+logazとなります。
もっと直感的には、例えば23×24=27となるので底を2としたときには
log2(23・24)=log223+log224=3+4=7と計算してよいという事です。
②逆数に関する対数の公式:
y=loga(1/x) とすると、ay=1/x
⇔ 1/(ay)=x ⇔ a-y=x ⇔ logax=-y=-loga(1/x)
もっと直感的には、2の3乗は8で、2の「-3乗」は1/8なので
log2(1/8)=-log28=-3と計算してよいという事です。
③対数の差に関する公式:
上記2つの公式を組み合わせると、
logax-logaz=logax+loga(1/z)=loga(x/z)となります。
④ベキ乗に対する対数の公式:
y=logax, z=loga(xb) とすると、ay=x, az=xb=(ay)b=ayb なので
z=yb つまりloga(xb)=blogaxです。
ここで(22)3=43=26のような計算をしています。
log2{(22)3}=3loga(22)=3・2=6のようになるという事です。
⑤「底の変換公式」:
これが最も分かりにくいかもしれませんが、使用頻度は少ないかもしれません。
理屈としては、次のように考えます。
logax=y, logbx=zとすると、ay=x, bz=x,
よってay=bzで、a>0, b>0なのでb=ay/zです。
これは「aのy/z乗がbになる」という事になり
logab=y/z=(logax)/(logbx)
⇔ logbx=(logax)/(logab) という底の変換公式になります。
例えば、log35=(log25)/(log23)という計算が可能であるという意味です。
途中の式でa=bz/yと考えると、logbx=(logax)(logba)という関係式になります。
これら2式の両辺の比を考えると、(logab)(logba)=1という関係も得られます。
logab=yつまりaのy乗がbである時、
bのy乗根(のうち正の数)がaなのでbを1/y乗すればaになる・・
つまりlogba=1/yとなるという事です。
具体的には、log28=3, log82=1/3より、(log28)(log82)=1といった計算です。