分数とは？

分数について初歩的な事項から説明します。

分数の考え方は、小学校だけでなく、中学・高校・大学と続けて使います。

基本的な考え方：半分の事を１／２と書く

分数【ぶんすう】とは、割合を２つの整数（１，２，３など）で表したものを言います。
例えば、「半分」の事を、「２つ分のうちの１つ」という意味で１／２【にぶんのいち】と書きます。
この１／２が、「分数」で表された数という事です。
「３等分したものの１つ」であれば１／３のように書きます。

分数は、次のように書いても同じものを表します。
教科書ではこのように書いてある事が多く、答案に書く時もこのようにする事を指導されるのが一般的です。

$$「２等分の１つ」\frac{1}{2}\hspace{20pt}「３等分の１つ」\frac{1}{3}\hspace{20pt}「４等分の１つ」\frac{1}{4}$$

１／２の、等分している数「２」を「分母」【ぶんぼ】と言います。
また、１／２の「１」を「分子」【ぶんし】と言います。
３等分したものを２つ集めると、２／３のような分数になります。２／３の分母は３、分子は２です。

１／２を３つ集めた３／２のような分数を考える事もできます。
１／２を「２ぶんの１」と読むのと同じように、３／２は「２ぶんの３」と読みます。
（２／３が「３ぶんの２」である事との区別に注意。）

半分が２つあれば、もちろん１になります。３等分したものを３つ集めれば１個に戻ります。これを式で書くと、１／２＋１／２＝１　あるいは (１／２)×２＝１という形になります。

$$\frac{1}{2}+\frac{1}{2}=\frac{1}{2}×2=1\hspace{20pt}\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1}{3}×3=1$$

分数の足し算は次のようにも書きます。

$$\frac{1+1}{2}=1\hspace{20pt}\frac{1+1+1}{3}=1$$

このように、「分母が同じ」分数は、分子だけで足し算や引き算を計算できます。

$$\frac{2}{5}+\frac{1}{5}=\frac{2+1}{5}=\frac{3}{5}\hspace{20pt}\frac{1}{4}+\frac{3}{4}=\frac{1+3}{4}=\frac{4}{4}=1$$

分数は本質的に「わり算」と同じ

「半分が２つ」あるとおおもとの１個に戻るので、もし「半分が４つ」あればおおもとの２個分になります。
「半分が６つ」あればおおもとの３個になります。
分子が「分母の数の倍数（２倍、３倍、４倍、・・）」であると、分数は整数に等しくなります。

$$\frac{2}{2}=1\hspace{20pt}\frac{4}{2}=2\hspace{20pt}\frac{6}{2}=3\hspace{20pt}\frac{8}{2}=4$$

$$\frac{3}{3}=1\hspace{20pt}\frac{6}{3}=2\hspace{20pt}\frac{9}{3}=3\hspace{20pt}\frac{12}{3}=4$$

これをよく見ると、分数とは「わり算」と同じ計算をしている事が分かります。
９÷３＝３、１２÷３＝４ですが、これを分数で９／３＝３、１２／３＝４と書いても同じ計算であるという事です。割り算で「あまり」がでる場合も含めて分数で表せるとも、言えます。５÷３＝「１あまり２」ですが、これを分数で書くと５／３と書けます。５／３＝３／３＋２／３と書く事もできて、「３等分」を基準にした時に確かに２個分のあまりが出る事が分かります。

１／２という分数をさらに２で割ると、「半分の半分」、つまり１／４になります。１／２という分数をさらに３で割ると「半分の３等分」が２つできるので、つまりおおもとの１に対して６等分（＝２×３）された数になります。このように、分数を割る時は「分母同士」をかける計算になります。

$$\frac{1}{2}÷2=\frac{1}{2}×\frac{1}{2}=\frac{1}{4}\hspace{20pt}\frac{1}{2}÷3=\frac{1}{2}×\frac{1}{3}=\frac{1}{12}$$

分数を分数でわる計算については「分子と分母を入れ替えてかける」という操作をします。この計算はつまづきやすい所かと思いますが、別途に詳しく説明しています。

「通分」の計算

１／３＋１／３＝２／３と計算できますが、１／２＋１／３という足し算はそのままではどのような数になるのかよく分かりません。この時、分母の２と３について、２の倍数でもあり３の倍数である数を考えます。
６は２の倍数でもあり３の倍数でもあるので、６を使って１／２＝３／６,　１／３＝２／６と考えて
１／２＋１／３＝３／６＋２／６＝５／６のように計算します。
この「分母を同じ数にそろえる」作業を「通分」【つうぶん】と言う事があります。

$$\frac{1}{2}+\frac{1}{3}=\frac{3}{6}+\frac{2}{6}=\frac{5}{6}\hspace{20pt}\frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}=\frac{7}{12}$$

３／７＋２／３のような計算も同じようにします。これを通分すると分母は２１になります。（３×７＝２１で見つけます。）この場合、分母に対する数と同じものを分子の数にもかけます。３／７の分母を２１にする時、分母を３倍しているので分子も３倍にします。

$$\frac{3}{7}+\frac{2}{3}=\frac{3×3}{21}+\frac{2×7}{21}=\frac{9+14}{21}=\frac{13}{21}$$

１／２＋１／３の計算で、２の倍数でもあり３の倍数でもある数は６だけでなく１２や１８もそうです。これらの数を使って「通分」して計算をしても同じ結果になります。（同じ結果になるので、普通は両方の分母の数の倍数であるもののうち「一番小さい数」を使います。）

$$\frac{1}{2}+\frac{1}{3}=\frac{6}{12}+\frac{4}{12}=\frac{10}{12}=\frac{5}{6}\hspace{20pt}\frac{1}{2}+\frac{1}{3}=\frac{12}{24}+\frac{8}{24}=\frac{20}{24}=\frac{5}{6}$$

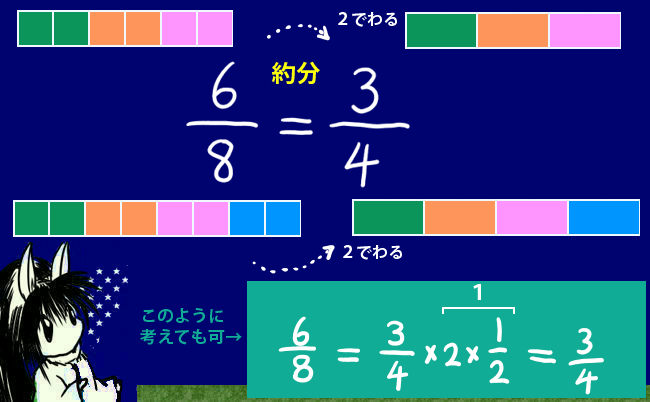
「約分」の計算

１０／１２＝５／６という計算では１０＝２×５、１２＝２×６なので、
２を基準にした時に１／６の５個分である５／６と同じになるという事を言意味します。
５／６に２をかけて２でわるともちろん５／６のままなので、
５／６＝(５／６)×２÷２＝１０／１２と考える事もできます。

$$\frac{5}{6}=\frac{5}{6}×2÷2=\frac{5}{6}×2×\frac{1}{2}=\frac{10}{12}$$

１０／１２のように、一般的に分母の分子に共通の倍数（「約数」【やくすう】）があるとき、その数で分母と分子の両方をわる事ができます。この操作を約分【やくぶん】と言います。
１０と１２は、どちらも２の倍数である（「２を『約数』に持つ」）ので、分母と分子にあるときは２で割ってよいという計算になります。２１／２７のような場合、分子と分母を３で割って７／９になります。

$$\frac{6}{8}=\frac{3}{4}\hspace{20pt}\frac{12}{15}=\frac{4}{5}\hspace{20pt}\frac{21}{27}=\frac{7}{9}\hspace{20pt}\frac{10}{100}=\frac{1}{10}$$