組み合わせの総数について説明します。順列と同じく「場合の数」の分野に属する個数の数え方です。これは確率でも使用しますし、2項定理を始めとして種々の計算にも使われる事が特徴です。
(英:組み合わせ【数学の用語として】 selection, combination)
考え方・・順番を区別せずに選ぶ
順列が並び方を区別するのに対して、
組み合わせは本当に「何を選んだか」だけを問題にして順番は無視するというものです。
例えば、4つのものを並べる順列の総数は4!通りですが、
4つのものから4つを選ぶ組み合わせは1通りだけです。
順列:{A,B,C,D}{A,B,D,C}{A,C,D,B}{A,D,C,B},・・他 24通り
組み合わせ:{A,B,C,D}の1通り
4つのものから3つを並べる順列の総数は4・3・2=24通りですが、組み合わせの場合はどうなるでしょう。具体的に書きだしてみると、{A,B,C}{A,B,D}{A,C,D}{B,C,D}の4通りだけという事になります。これを記号では4C3=4のように書きます。
尚、4つのものから3つを選ぶという事は実際のところ「残る余りの『1つ』」の選び方と同じなので、ただちに「4通り」と言う事もできます。これは次に触れるように、公式のような形で定式化する事もできます。

「並び方を区別しないのだから組み合わせのほうが簡単か?」というと、「その総数」が組み合わせの場合のほうが少なくなるのは正しいです。
ただし、考え方としては多分順列のほうが簡単で、順列を理解してから組み合わせを考える方が学習の手順としては便利です。
結論の式と公式
公式にすると、結論は次のようになります。
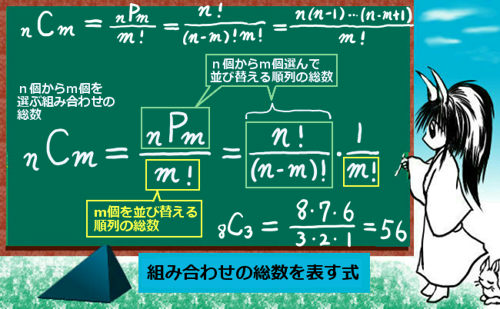
n個の中からm個を選ぶ「組み合わせ」の総数をnCmの記号で表し、次式のように計算できます。$$_nC_m=\frac{_nP_m}{m!}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}=\frac{n!}{(n-m)!m!}$$ここで、等号で結ばれてる部分は式変形しているだけで、どの方法で計算しても良いという事です。nPmは順番を区別した「順列の総数」を表します。
特に、m=n、m=1の場合や、n-m個を選ぶ場合には次式が成立します。$$_nC_n=1\hspace{20pt}_nC_1=n\hspace{20pt}_nC_{n-m}=_nC_m$$
この組み合わせの記号nCmを2項係数と呼ぶ事もあります。(名称が違うだけで中身は全く同じです。)
その名称の由来は冒頭で触れましたように、2項定理で係数として表される事によります。
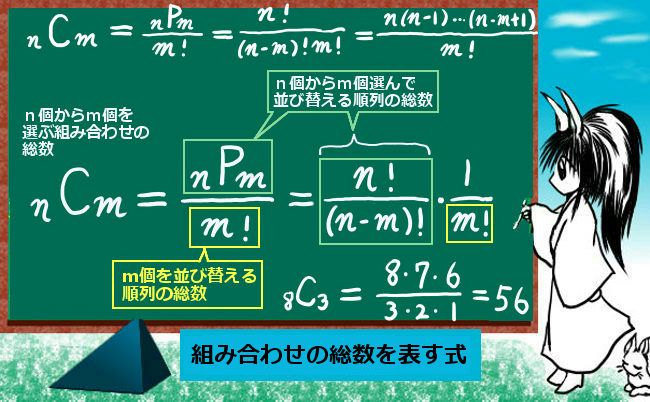
考え方としては次のようにします。
まず、n個からm個を選び「並び替える」場合はnPm通りです。この時、「n個からm個を選ぶ」という操作はじつはすでにやってしまっているんですね。
ただし順列の場合は、その「選んだm個の並び替え」も実行して、総数にカウントしているわけです。言い換えると、順番を区別していない「組み合わせ」のそれぞれを「m個を並び替変えの総数:m!通り」倍しているわけです。
例えば、5つから3つを選んで{A,C,D}であったとしましょう。これは、順番を区別していないものです。つまり、{C,A,D}と書いても同じものとします。
ここで、順列の場合は、{A,C,D}の並び替えもカウントするので、この組み合わせに対して3!=6通りあるわけです。
これは他の組み合わせ{B,C,E}などに対しても並び替えれば3!=6通り発生するわけで、他の組み合わせも個体の数が同じですから同様に並び替えで3!=6通りずつ発生します。
結局、次のようになります:
「組み合わせの総数【nCm】」×「選ぶ個数【m】に対する順列の総数【m!】」
=「n個からm個選んで並び替える順列の総数【nPm】」
という事になります。これを式で書くと次のようになります。
$$(_nC_m)\cdot (m!)=_nP_m\hspace{5pt}\Leftrightarrow \hspace{5pt}_nC_m=\frac{_nP_m}{m!}$$
これが、組み合わせの総数を表す公式の意味です。
この式の続きは、単なる分母と分子の約分の計算になります。順列を階乗だけで表す形にすれば組み合わせの式もnとmを使った階乗で表される形になります。
この式を使えば、例えば7個から3つ選ぶ場合の組み合わせの総数は、次のようになります。
$$_7C_3=\frac{7\cdot 6\cdot 5}{3!}=\frac{7\cdot 6\cdot 5}{3\cdot2\cdot1}=35$$
このように「35通り」という結果が比較的簡単に分かるわけです。尚、これが順列であれば6倍の210通りですから、並び替えずに組み合わせにすると大きな数に比較的なりにくい傾向がある事も分かります。
ここで、同じ組み合わせを階乗だけの形で書くと、
$$_7C_3=\frac{7!}{(7-3)!3!}
=\frac{7!}{4!3!}$$
他方、7つから4つ選ぶ組み合わせの総数は、
$$_7C_4=\frac{7!}{(7-4)!4!}
=\frac{7!}{3!4!}$$
であり、これらは同じ数ですね。7個から3つ選ぶ場合も4つ選ぶ場合も、同じく35通りです。これは、3つ選んだら残り4つも必然的に決まるのだから同じ総数になって当然であると考えてもよいですし、一般のnとmに対する式変形で示す事も可能です。
式で示す場合、n個から(n-m)個を選ぶ組み合わせの式を作ってみればよいのです。
$$_nC_{n-m}=\frac{n!}{\{n-(n-m)\}!(n-m)!}=\frac{n!}{m!(n-m)!}= _nC_m$$
分母のところの掛け算が順番を入れ替えても同じになる事から、この関係が成り立ちます。つまり、7個から2個選ぶ組み合わせの総数が分かったら、7個から5個選ぶ組み合わせの総数も同じであるので計算不要という事です。(順列の場合は、そのようにする事はできません。)
必ず自然数になる?
さてここで、言われると確かにそのように納得できるかもしれないが、順列の総数を「m!」で割る時に「自然数になる」保証はあるのか?と思うかもしれません。
これは「理解」する方法としては、「組み合わせの総数が1.5通りとか2/3通りになる事はあり得ないので、必ず自然数であるに決まっている」・・と、捉えても支障はありません。
実際、どうやっても自然数にしかならないからです。
他方で、順列とか組み合わせとかを離れて、単に自然数nとmを持ってきて次式が自然数になるか否かという問題が提示された時に「組み合わせだから自然数」と言うのは数学的な証明には、もちろんなりません。
n、mを自然数(n≧m)として $$\frac{n!}{(n-m)!m!}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}$$ (これが「組み合わせの総数」を表す前提はないものとして)
結論は、この式は必ず自然数になります。分子は分母で必ず割り切れて余りはでないという事です。
そのようになる事に対する一番簡単な証明は、「順番にn個並んだ自然数の中には、nの倍数が少なくとも1つ必ず含まれている」という事を根拠にするものです。
例えば、順番ずつ3つ並んだ自然数の中には、3の倍数が少なくとも必ず含まれています。これは、どんなでたらめな自然数を持ってきても、それに+1、+2する形(あるいは-1、-2)する形で並べてあげると3の倍数が必ず含まれるという事です。
214というてきとうな自然数をもってきて、{214、215、216}と並べれば、この場合は真ん中の数が3の倍数ですね。この理屈の意味自体は簡単で、1,2,3,4,5,6,7,8,9,・・・と、並べたとき、どこでもいいから数が3つ含まれるように区切ると、どうやっても3の倍数は1個以上含まれるという事です。

3でなくても、5でも6でも7でも、任意の自然数でそのようになります。
もう少し一般的に言うと、例えば3の倍数なら、任意の自然数は3n, 3n+1, 3n+2 のいずれかで表されるので1を加えていくか引いていく形で3個並べれば、その必ず3nの形のものが存在するという事です。
$$_nC_m=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}$$
の形で見るのが一番分かりやすいかと思いますが、式の分子の(積の)項数はm個です。他方、分母はm!=m(m-1)(m-2)・・・3・2・1ですから、m以下の自然数しか含まれません。そのため、分子に含まれる任意の自然数の倍数は、必ず分母に存在するという事です。これが基本的な考え方です。
話が少しややこしくなるのは、組み合わせの式の場合では分子に複数の自然数があるためです。仮に自然数pとqの倍数が共通する数として分母に含まれていたら、必ず割り切って全体として自然数になるかが怪しくなる可能性もあるとも言えるわけです。
しかし実際はそのような事は起きないので大丈夫であるというのが結論です。
まずnは固定したうえで、mまでは確かに割り切れて全体が自然数になるとしましょう。
次のm+1が素数であったら、mまでの数のいずれでもないし倍数でもないので、分子のm+1個の中にm+1の倍数が存在し、割り切れる事になります。
m+1が素数でない場合で、m以下の自然数pの倍数になっている時であっても、例えばpq個の中には、pの倍数が少なくとも「q個」含まれています。これは、p個の塊で区切れるところがq個あるためです。
そのうえで、pqの倍数も1個以上あるので、分母の1つのpの倍数を既に割って使ってしまったあとでも別のpの倍数が必ず残っています。それで、m+1=pqの倍数も分母に必ずあるので、再び全体として割り切って自然数になるというわけです。
具体例では、8C3=8・7・6/(3・2・1) は確かに自然数になりますが、続いて8C4を考えた時に、8C4=8・7・6・5/(4・3・2・1)の分母に新たに入った4=22について、すでに分母にある2については、分母の項数が4つなので、2の倍数は2個以上あります。(この場合、見れば分かる通り6と8です。)分母の4項の中で、4の倍数は必ず1個以上ある事は確定しています。
A,B,C,Dと並べたところの1つが4の倍数だと考えると分かりやすいかと思いますが、例えばBの位置にあったとき、C、Dは使用しませんが、2の倍数は2個ずつ区切ったA,BとC,Dのどちらにも1個ずつ含まれます。このようにして、分母にすでに2がある事で4で割り切れなくなってしまう心配はないという事です。
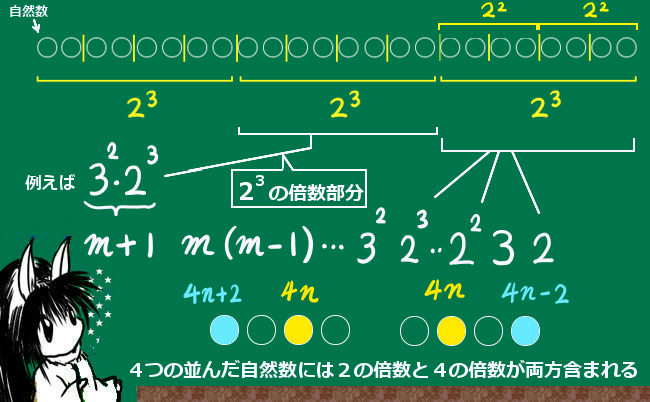
9個の続く自然数には3の倍数と9の倍数がどちらも必ず含まれます。
少しややこしい理屈である事は間違いありませんが、基本的な考え方は一般のnとmに対しても同じ事です。
このようにして、組み合わせの総数を表す式はきちんと「割り切れて」自然数になる事が式の形からも保証されます。
別の方法はある?
「組み合わせを順列を使って表せるのは分かったが、別の方法はないのか」
あります。場合の数を考える時には考え方は1つとは限らず、複数の考え方で同じ結論になる事はよくあります。ただし、組み合わせに関して言えば順列を階乗で割る表し方が一番簡単ではないかと思います。
別のやり方としては、1つの例として次のように組み合わせを考える事もできます。
A,B,C,D,E,F,Gの7つから4つ選ぶ場合、まず「Aを含む場合」、残り3つを6つから選びます。次に、Aを含まずBを含む場合、A,Bを含まない5つから3つを選びます。
こういう具合に考えても組み合わせの総数を表す事ができて、次の関係が成立します。
$$_nC_m=_{n-1}C_{m-1}+_{n-2}C_{m-1}+_{n-3}C_{m-1}+\cdots +_{m}C_{m-1}+_{m-1}C_{m-1}$$
6つから3つを選ぶ組み合わせは、さらに5つから2つを選ぶ場合・4つから2つを選ぶ場合・・に分割できます。数が少なくなれば「明らかに」分かる組み合わせの場合にたどり着きます。
7つから4つ選ぶ時に実際にこれが正しいのかを見てみると、
$$_7C_4=_{6}C_{3}+_{5}C_{3}+_{4}C_{3}+_{3}C_{3}=20+10+4+1=35$$
通常の組み合わせの公式で計算すると、
$$_7C_4=\frac{7\cdot 6\cdot 5\cdot 4}{4\cdot 3 \cdot 2 \cdot 1}=35$$
この通り一致するわけですが、これは次の理由になります。
まず分母の7を(4+3)の形に書きます。
$$_7C_4=\frac{(4+3)\cdot 6\cdot 5\cdot 4}{4!}=\frac{4\cdot 6\cdot 5\cdot 4+3\cdot 6\cdot 5\cdot 4}{4!}=\frac{6\cdot 5\cdot 4}{3!}+\frac{3\cdot 6\cdot 5\cdot 4}{4!}$$
$$=_6C_3+\frac{3\cdot (4+2)\cdot 5\cdot 4}{4!}=_6C_3+\frac{4\cdot 5\cdot 4\cdot 3+2\cdot 5\cdot 4\cdot 3}{4!}=_6C_3+_5C_3+\frac{2\cdot 5\cdot 4\cdot 3}{4!}$$
$$=_6C_3+_5C_3+\frac{2\cdot (4+1)\cdot 4\cdot 3}{4!}=_6C_3+_5C_3+_4C_3+\frac{ 3\cdot 2\cdot 1}{3!}=_6C_3+_5C_3+_4C_3+_3C_3$$
一般のnとmの場合も同じで、分母の一番大きい項を(m+p)の形にして分離していくとこの形になります。
しかし言い換えると、この考え方でやったとしても結果は同じでnCm=(nPm)/(m!) と同じ式になるのです。