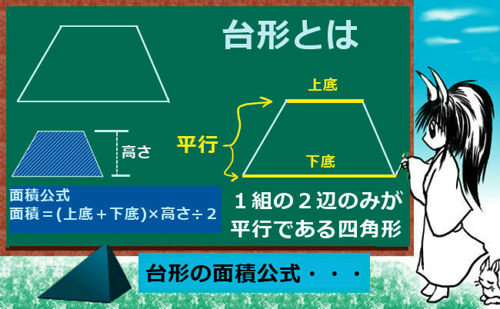
小学校や中学校で教わる台形の面積を出すための公式というものがありますね。
台形の面積={(上底)+(下底)}×(高さ)÷2
これくらいなら覚えれるという人も多い一方で、なんでこんな変な公式になるのか疑問に思いながら覚えた人も中にはいるかもしれません。この公式がなぜ成立するのかをこのページでは述べます。理由は全く難しくありません。
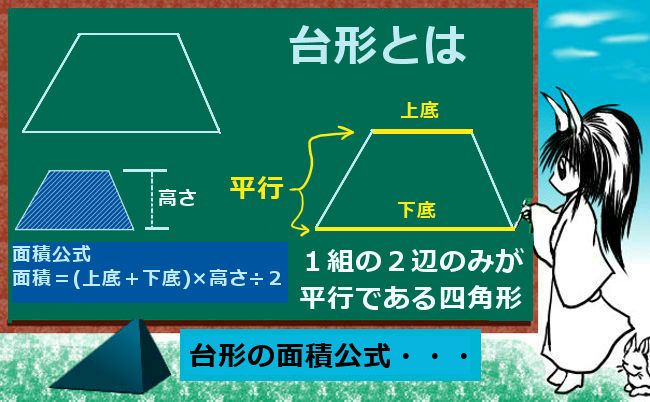
台形の面積公式の導出方法はじつにシンプルで、
「台形をコピーして上下左右ひっくり返してぴったり貼り付けると平行四辺形になる」
なんとこれだけです。
まず、もとの台形を上下・左右逆さまにひっくり返したものを用意します。まず上下に反転し、左右にも反転させる事が1つポイントです。
これを、もとの台形の横にくっつけます。
尚、「ぴったり」きれいに必ずくっつくという事は平行線の錯角の関係によって保障されるのです。
すると、平行四辺形の面積は(底辺)×(高さ)であるわけですが、この大きな平行四辺形の「底辺」は、台形の(上底)+(下底)なのです。下底に、上底だった部分がくっついていますので。
ただ、その平行四辺形の面積は台形2個分の面積です。
そのため、もとの台形の面積はその半分であって、「2で割る」わけです。
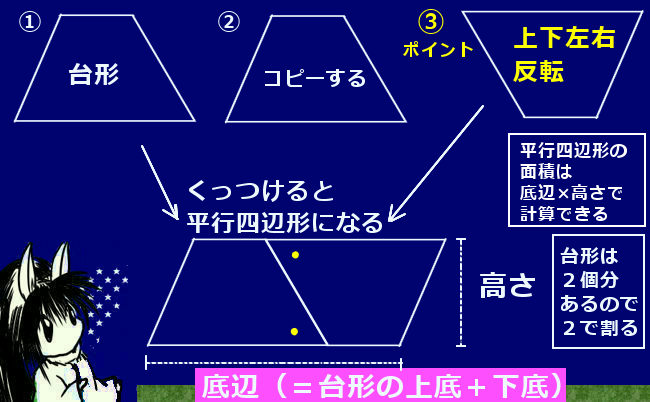
これで、公式「台形の面積={(上底)+(下底)}×(高さ)÷2」が出ます。【証明終り】
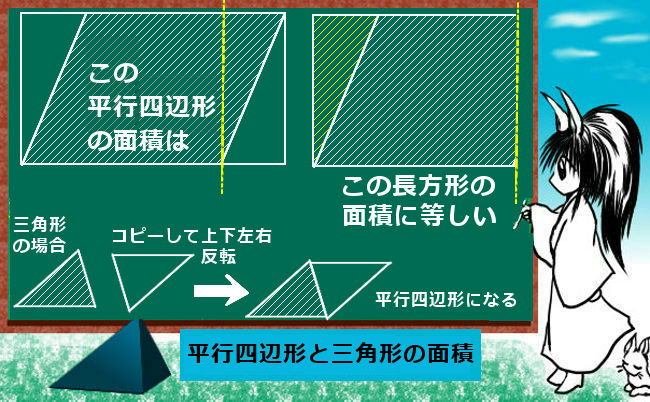
尚、三角形の面積公式も三角形2つで平行四辺形を必ず作れる事に由来します。
「2で割る」というのは、じつは台形の場合と同じ理由であるわけです。
また、平行四辺形の面積が(底辺)×(高さ)となる理由は、出っ張っている部分を切り取って反対側につけると「長方形」になるためです。
さらに言うと、長方形の面積は正方形の面積の和に最終的には還元されます。
面積の単位は「平方メートル」m2(あるいは平方センチメートルcm2)と書きますね。つまり面積というものは1m2の正方形が何個分あるかという事なのです。もちろん、それを数えるのは大変ですから、面積の公式というものを使うわけです。
台形の面積公式の場合は、言われれば覚えれる人も多いと思います。ただ、たまには、どういう理由でそうなってるのかを考えてみると楽しい事もあるかもしれません。
尚、こういった初歩的な面積計算は、高校や大学での積分の理論の基礎になっています。