複素数の積分 | 理数系学習サイト　kori

複素数の微分に続いて、このページでは複素数の積分について述べます。
これは学校での授業としては大学数学の範囲になります。

定義と考え方

複素関数の微分は比較的分かりやすいかと思いますが、
では複素関数のの積分は一体どのように定義するのかという話になります。

考え方は、実数関数の積分と同じく、「和」を考えます。

ｚ＝ｘ＋ i ｙのときに、ｄｚ＝ｄｘ＋ i ｄｙを考えるのです。

そして、複素関数ｆ(ｚ)に対してｆ(ｚ)ｄｚ＝ｆ(ｚ)ｄｘ＋i ｆ(ｚ)ｄｙを考え、加え合わせます。
これが複素関数の積分です。

複素関数の積分（定積分）

$$\int_Cf(z)dz=\int_Cf(z)(dx+idy)=\int_C(u+iv)(dx+idy)=\int_C(udx-vdy)+i\int_C(vdx+udy)$$

ｆ(ｚ)＝ｕ(ｘ,ｙ)＋iｖ(ｘ,ｙ)です。
積分記号に添えられているＣとは、後述する「積分経路」です。

ｘとｙが媒介変数ｔ(実数)で結ばれる時は、このｔによって複素変数ｚが定まるので、ｔによる積分と考える事もできます。

これら２つの複素関数の積分の定義は同等なものとなります。

媒介変数を使った複素関数の積分（定積分）

$$\int_Cf(z)dz=\int_a^bf(z(t))\frac{dz}{dt}$$

この場合、媒介変数ｔは実数です。
ｔの積分区間 [a, b] において、あたかも通常の実関数であるかのように定積分を行う事になります。
積分経路が円の時は、媒介変数として弧度法の角度θを使う事が多いです。

さて、実数関数の場合の定積分には「積分区間」がありました。複素関数の場合にもそれに相当するものがありますが、じつは積分の区間ではなく「経路」が必要になります。

単純にｘを動かして次にｙを動かした場合、それは多くある積分経路の１つです。

積分経路は、直線であったり、曲線であったり、円のような閉曲線でもあり得ます。

このような積分経路が定められた時、ｚ＝ｘ＋ i ｙのｘとｙには従属関係があります。

$$例えば直線であればy=2x,円であればx^2+y^2=1といった関係です。$$

このような時には媒介変数ｔでｘとｙを結ぶ事ができます。円の場合には、媒介変数は角度で考える事が普通です。

積分経路上の１つ１つの点に対して、複素関数ｆ(ｚ)の値が存在する形になります。

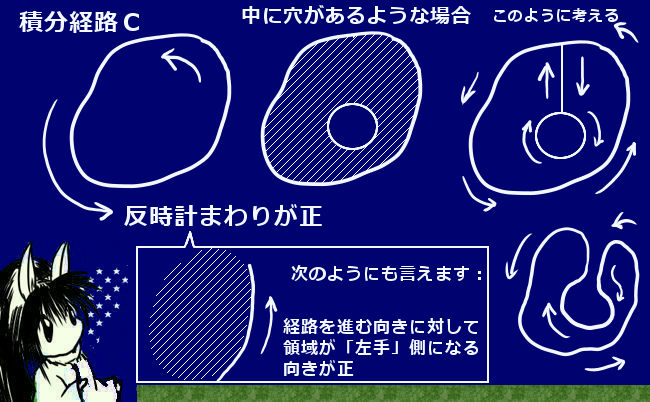
積分経路が閉曲線の場合、基本的には「反時計回り」が正の方向です。もう少し詳しく言うと「経路を進む方向に対して領域が常に左側に来るように」正の向きをとります。

この向きの取り方は閉曲線の中に別の閉曲線による「穴が」あるような場合の正の向きの考察に役立ちます。（そのような場合も一番外側の閉曲線を「反時計回り」で考える事で正しく向きを処理する事も可能です。）

複素数の積分は間接的に物理等の理論に関わり、数学上も時折使う事のあるツールの１つとしてところどころで顔を出します。

まず１つは、特定の実数関数の定積分（多くの場合積分区間を無限大にする「広義積分」ですが）の値を出すのに、複素積分を使う事があります。あるいは、そのような手順を踏まないと手計算では値を出せないと言ったほうがよいでしょう。そういった種類の定積分があるわけです。

もう１つは、分母に変数があり、その変数が０になってしまう場合（「極」と言います）の処理のために複素積分の考え方をうまく使える場合があります。これについては「コーシーの積分公式」との関連が深いです。

数学の理論の中では「代数学の基本定理」について、複素数の積分の理論の一部を適用する事によって証明が可能です。（他の方法でも証明はできます。証明の方法は多いです。）