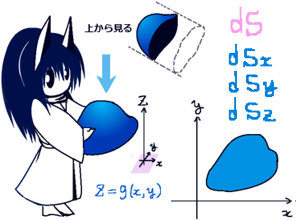
積分変数としての面積要素dSと、x、y、zで積分した時に使うdx、dy、dzを偏微分を使って結びつける公式について説明します。
積分変数に関する公式ですからもちろん積分に関係しますが、ベクトルとも関連します。
この公式はやや特殊で、使われる場面はベクトル解析の分野のごく一部分に限定されるとも言えます。しかし特定の定理の証明・考察において重要である場合があるので、詳しく解説しておきます。
■より初歩的な内容(内部リンク):
- ベクトルの考え方:スカラーとの違い(ベクトルの初歩事項の解説)
- 偏微分の定義と公式(このページの公式中で使います。)
- 外積ベクトルの定義と公式(「クロス積」「ベクトル積」とも。知っておくと便利です。)
- 積分の考え方と基本計算(1変数の積分の具体例です。)
面積要素とは
法線面積分においては曲面上の微小な領域に対する法線ベクトルを考えて、その法線ベクトルの大きさはその微小領域の面積であるとします。
そして、その面積にプラスマイナスの符号があると考えた量を特に面積要素(あるいは面積元素)と呼ぶ事があります。面積要素はdSなどの記号で書かれます。
式で書くと次のようになります。
各成分は対象の曲面上の微小領域をyz平面、xz平面、xy平面へ射影した領域の面積です。$$d\overrightarrow{S}=(ds_x,ds_y,ds_z)$$
この法線ベクトル\(d\overrightarrow{S}\) の事を特に指して「面積要素ベクトル」と呼ぶ事もあります。
面積要素の絶対値は、このベクトルの大きさに等しいものとします。 \(|dS|=|d\overrightarrow{S}|\)
※「面積ベクトル」という用語は、曲面全体に対する単位ベクトルの法線面積分の事を指す場合があります。
また、法線面積分を考える時には「ベクトル場と単位法線ベクトルの内積を考え、それに面積要素を乗じるという形の形で書く」という形式もあります。ここで言う単位法線ベクトルとは「大きさが1」の法線ベクトルという事です。
法線面積分の計算を進める時には、内積を計算する形で成分ごとに分解した積分を考える事がありますが、その時に考える「スカラー場に対して、yz平面、xz平面、xy平面内の領域の面積要素を積分変数とする」形の積分を単に「面積分」と呼ぶ事もあります。
変換の公式
面積要素dSと、面積要素ベクトルの成分dsx、dsy、dszの間には実は変換の公式が存在し、それは曲面を表す関数に対する偏微分を使って表されます。
今、曲面を表す関数としてzがz=g(x,y)のような形で表されているとします。(これはベクトル場の成分を表す関数ではなくて、曲面を表す式です。)
$$dS=ds_z\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}$$ $$ds_y=-\frac{\partial z}{\partial y}ds_z$$ $$ds_x=-\frac{\partial z}{\partial x}ds_z$$ この公式を使う時には、曲面を多面体とみなした時に微小な三角形(あるいは平行四辺形)の2辺がそれぞれxz平面上およびyz平面上にあるような分割を考えています。 (法線面積分および面積分の値は分割の仕方には依存しません。)
上記の式を組み合わせて、dsyとdsxについても面積要素dSとの関係式を作る事が可能です。
これらは決して使いやすい形の公式とは言えないかとは思いますが、ベクトル解析における特定の定理の証明等で使える場合もあります。
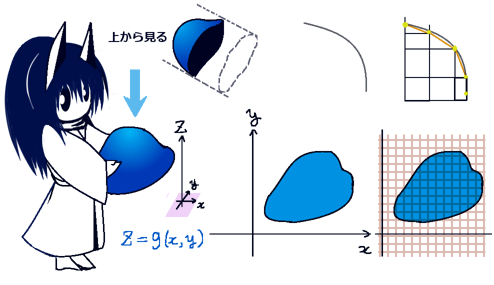
偏微分を使った面積要素の変換公式を考える時には
座標軸に平行な直線で区切った長方形の分割を行っています。
曲線上になっている部分は折れ線で近似して直角三角形の分割として考えます。
◆! 注意点・・・
これらの公式はあくまで
「法線面積分およびスカラー場に対する面積分における、
積分変数としての面積要素に対して成立する変換公式」であり、
通常の二重積分等での積分変数の変換(極座標変換など)では使う事はできません。
二重積分や多重積分で積分変数の変換を行う時には、関数行列式を使った変換が必要です。
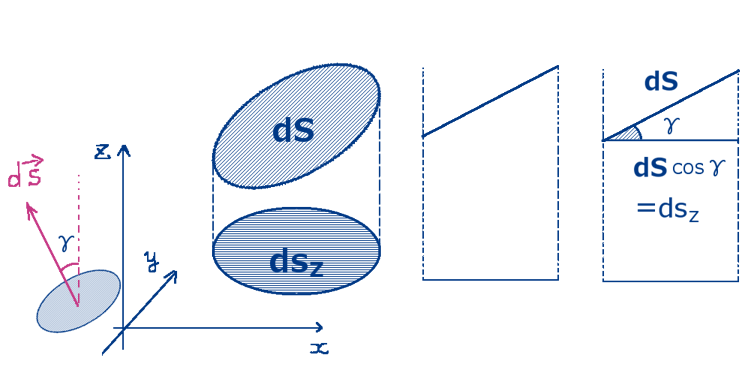
また、dsx/dS,dsy/dS,dsz/dSは図形的に余弦とみなす事ができて、方向余弦とも呼ばれます。(方向余弦は面積要素ベクトルに対してだけでなく、ベクトル一般に対して考える事ができます。)これらの面積要素ベクトルの方向余弦は、分割の方法を合わせるという前提のもとで上記の公式中の係数で表す事ができます。
※余弦とは三角関数の「コーサイン」「cos」の事です。
角度は鋭角の場合であるとします。
$$\frac{ds_x}{dS}=\cos\alpha,\hspace{10pt}\frac{ds_y}{dS}=\cos\beta,\hspace{10pt}\frac{ds_z}{dS}=\cos\gamma \hspace{10pt}と置いた時、$$
(※これらは導関数の記号ではなく、普通の「割り算」あるいは「比」を考えています。)
$$\cos\alpha=-\Large{\frac{\frac{\partial z}{\partial x}}{
\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}
}}$$
$$\cos\beta=-\Large{
\frac{\frac{\partial z}{\partial y}}{
\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+
\left(\frac{\partial z}{\partial y}\right)^2}
}
}$$
$$\cos\gamma=\frac{1}{\Large{
\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}
}}$$
曲面の分割は、前述の変換の公式を適用する時と同じであるとしています。
また、\(dS\cos\alpha=ds_x\), \(dS\cos\beta=ds_y\), \(dS\cos\gamma=ds_z\) でもあります。
角度が鈍角の場合にはプラスマイナスの符号が変わります。
公式の導出および証明
上記の公式の証明においてはベクトル場の事は考えず、曲面の事だけを考えます。
面積要素と、面積要素ベクトルの第3成分との関係式の証明
曲面Sの領域の分割が、xy平面への射影を考えた時に辺がx軸とy軸に平行な長方形になるように考えます。曲面の外周部分に関しては長方形を対角線で区切った直角三角形を考えます。
この時に分割された各領域は、1つの共有点を始点(原点と考えます)に持つxz平面上のベクトルと、yz平面上のベクトルを2辺として構成されていると考える事ができます。
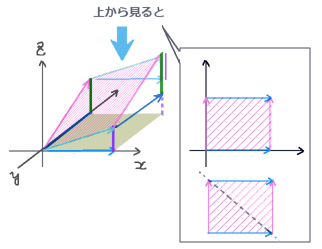
それらの2つのベクトルを \(\overrightarrow{a}\) および \(\overrightarrow{b}\) とおきます。
(位置関係は、dxとdyの符号がともにプラスである時に外積ベクトルがz軸のプラス方向を向くようにします。その側が面の表側で、面積要素ベクトルが出る側として考えます。)
今、曲面の各点のz座標はz=g(x,y)のような関数で表せる事に注意すると、
2つのベクトルはzに対するxとyでの偏微分を使って表せます。
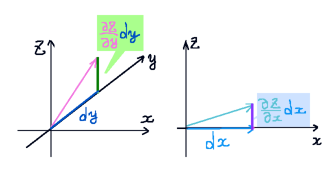
\(\overrightarrow{a}\) の(終点の)x座標をdxとして、\(\overrightarrow{b}\) のy座標をdyとすると、次のように書けます。
$$\overrightarrow{a}=\left(dx,0,\frac{\partial z}{\partial x}dx\right),\hspace{15pt}\overrightarrow{b}=\left(0,dy,\frac{\partial z}{\partial x}dy\right)$$
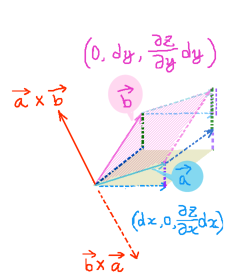
そのため、1つのベクトルはy成分が0で、もう片方のベクトルはx成分が0です。
この時にこれら2つのベクトルにより構成される平行四辺形の面積(|dS|に等しい)は、公式を使って次のように表されます。対角線で区切った三角形の面積ならその半分になります。
$$dS=\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2}$$
$$|ds|=\sqrt{ \left\{dx^2+\left(\frac{\partial z}{\partial x}\right)^2dx^2\right\} \left\{dy^2+\left(\frac{\partial z}{\partial y}\right)^2dy^2\right\} -\left(\frac{\partial z}{\partial x}\right)^2 \left(\frac{\partial z}{\partial y}\right)^2dx^2dy^2 }$$
【平方根の中の2つの項がちょうど同じ値で引き算されて0になります。】
$$=\sqrt{dx^2dy^2+dx^2dy^2\left(\frac{\partial z}{\partial y}\right)^2+dx^2dy^2\left(\frac{\partial z}{\partial x}\right)^2}$$
ここで、平方根の中のdxdyについて2乗した形が共通してどの項にもあるのでdxdyを平方根の外に出す事もできますが、敢えてひとまずこのままにしておきます。
面積要素ベクトルの第3成分(z成分)のdszの絶対値は、微小領域をxy平面に射影した領域の面積になります。【その証明は外積ベクトルの定義からの計算と、平面上のベクトルを使った平行四辺形の面積公式から行います。】
今、微小領域をxy平面に射影すると長方形になるように分割を考えています。
よって、|dsz| = |dxdy| と書けます。【外積ベクトルのz成分を考えても同じ事です。】
すると dsz2 = dx2dy2 という事にもなるので、
これをさきほどの計算式に代入します。
$$|dS|=\sqrt{ds_z^2+ds_z^2\left(\frac{\partial z}{\partial y}\right)^2+ds_z^2\left(\frac{\partial z}{\partial x}\right)^2}$$
ここで、dszはプラスとマイナスの両方の符号の場合があり得ます。これは図形的には、実は単純な話です。面積要素ベクトルがz軸のプラス方向側に向いていればそのz成分であるdszの符号もプラスで、逆に面積要素ベクトルがz軸のマイナス方向側に向いていればそのz成分であるdszの符号もマイナスという事になります。
すると、上式ではdszを平方根の外に出す事ができますが、それが式の右辺のプラスマイナスの符号を決める唯一の量になります。よって、面積要素dSの符号はdszによって決定する事になります。式で書けば次のようになります。これで証明完了です。
$$dS=ds_z\sqrt{1+\left(\frac{\partial z}{\partial y}\right)^2+\left(\frac{\partial z}{\partial x}\right)^2}$$
ここでの符号の問題についてはdxとdyを基準に考える事もできます。
外積ベクトル \(\overrightarrow{a}\times \overrightarrow{b}\) が面積要素ベクトルに等しいと考えると、
そのz成分はdsz=dxdyー0・0=dxdyで、符号まで一致している事になります。
この時、仮にdxとdyのどちらかがマイナスになると位置関係的にも、
外積ベクトル \(\overrightarrow{a}\times \overrightarrow{b}\) はz軸のマイナス側を向く事になります。
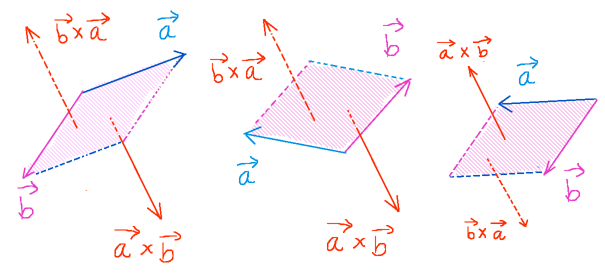
片側だけ符号を反転させた場合のみ、外積ベクトルの方向も反転します。
この外積ベクトルが面積要素ベクトルに等しいと考えれば、
面積要素ベクトルの第3成分とdxdyの符号が一致するようになります。
面積要素ベクトルの第1成分と第2成分についての式の証明
次に、面積要素ベクトルの第1成分(x成分)と第2成分についての式も考えます。
それらを表すには外積ベクトルとして成分を計算したほうが簡単で、次のようになります。
$$再度記すと\overrightarrow{a}=\left(dx,0,\frac{\partial z}{\partial x}dx\right),\hspace{15pt}\overrightarrow{b}=\left(0,dy,\frac{\partial z}{\partial x}dy\right)としているので、$$
$$ds_x=0\cdot\frac{\partial z}{\partial y}dy- \frac{\partial z}{\partial x}dx\cdot dy=-dxdy\frac{\partial z}{\partial x}$$
ここで使っている公式は次のものです。
$$\overrightarrow{a}=(a_1,a_2,a_3),\hspace{10pt}\overrightarrow{b}=(b_1,b_2,b_3)\hspace{10pt}のもとで$$
$$\overrightarrow{a}\times \overrightarrow{b}=(a_2b_3-a_3b_2,\hspace{5pt}a_3b_1-a_1b_3,\hspace{5pt}a_1b_2-a_2b_1)$$
外積ベクトルの各成分の絶対値は、2つのベクトルを2辺とする平行四辺形を
yz平面、xz平面、xy平面に射影した領域(それも平行四辺形。この記事内での例では長方形)の面積に等しくなっています。
ここで、先ほどの証明の最後で触れましたが面積要素ベクトルを外積ベクトルとして表した場合には符号まで一致してdsz=dxdyと表す事ができるので、それをそのまま代入する事ができます。すると次のようになって、示すべき式が得られます。
$$ds_x=-\frac{\partial z}{\partial x}ds_z$$
面積要素ベクトルの第2成分についても同様に、
外積ベクトルの成分として計算すると次のように示すべき式を得ます。
$$ds_y=\frac{\partial z}{\partial x}dx\cdot 0\hspace{3pt} – dx\cdot\frac{\partial z}{\partial y}dy=-dxdy\frac{\partial z}{\partial y}$$
$$よって、ds_y=-\frac{\partial z}{\partial y}ds_z$$
この面積要素の変換公式は、ストークスの定理に対する証明の1つの過程で使用する事ができます。