このページでは分数の割り算について述べます。
内容としては小学校でやる算数ですが、計算の仕方の『理由』について分かりやすく述べます。
分数の割り算の計算方法
■ 分数の割り算:ひっくり返して掛け算しよう
■ ある映画の場面:計算の理由を問いただす少女と、怒りだす姉
分数の割り算:ひっくり返して掛け算しよう
分数の割り算をする時は、分母と分子を入れ替えて掛け算をします。
例えば次のようにします。
$$1 ÷ \frac{1}{3}=1 ×\frac{3}{1}=3$$
$$2 ÷ \frac{2}{3}=2 × \frac{3}{2}=3$$
ある映画の場面:計算の理由を問いただす少女と、怒りだす姉

昔、こんなアニメ映画の場面がありました。
小学生の女の子が、姉から算数の勉強を家で教わるのですが、女の子が「分数の割り算は『なぜ』ひっくり返して掛け算になるのか」と問いただし始めます。
その場面で姉の返答はどういうものであったかというと、机を叩き
「ひっくり返して掛け算するって決まってるのよ!!」
その場面は、それで終わりです。ある女性が子供の頃を回想する場面だったと思いますが、結局『なぜ』に対する答えは語られる事のないまま終わります。
ここでは、『なぜ』に対する答えを考えてみましょう。
理由はじつに簡単なもので、駄々をこねた女の子が悪かったのかというとそうではなくて、おそらく女の子も姉も両方とも、あまり良い形で算数や数学を学校で教えてもらっていなかったと解釈できるかもしれません。
考え方①:「1個の中に半分個はいくつありますか。」
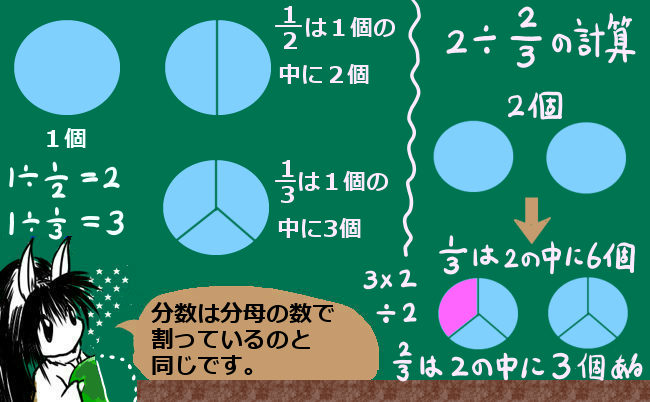
\(1÷\frac{1}{2}\) の型の計算
一番簡単だと思われる考え方は次の通りです。
1個の中に、半分個はいくつあるでしょう。もちろん2個ですね。
これが、1÷(1/2)=2であるという事です。
では、1個の中に3等分した(1/3)個はいくつあるでしょう?もちろん、3個あるのです。
これが 1÷(1/3)=3であるという事です。
もうお分かりかと思いますが、数がいくつでも同じ事であって、例えば1個の中に(1/100)は100個あります。
数がもっと大きくても、中途半端な数でも同じです。
$$1÷\frac{1}{721}=1×721=721$$
つまり、次のように計算してよいわけです:
$$1÷\frac{1}{N}=1×N=N$$
また、1『個』でなくとも、1kgでも1メートルでも、何でも同じ事ですね。
2や3を1/2などの分数で割る時は、例えば 2÷(1/2)については1個の中には半分個が2つあり、それが2個あるのですから 2÷(1/2) =2×2 =4であるわけです。
$$A÷\frac{1}{N}=A×N$$
\(1÷\frac{2}{3}\) の型の計算
では、1を2/3で割る場合はどうでしょうか。
この場合も、計算の工夫をするだけで、考え方は同じなのです。
まず、1を3等分します。すると、1/3は3個あります。これは、前述の1÷(1/3)=3の計算に該当します。
次に、3の中に、2はいくつあるかというと、3/2です。小数で表すならこれは1.5です。
つまり、
$$1÷\frac{2}{3}=1×3÷2=1×\frac{3}{2}= \frac{3}{2} $$
と、いう事です。
計算の途中で、確かに「ひっくり返して掛け算」になっていますね?
ようするに、1÷(2/3)は、「1/3の2倍」が1の中に何個あるかを調べる計算であり、手順としてはまず分母を掛け算し、次に分子で割ればよいという事なのです。
整理すると、次のような形です。
- 分母の数で等分する事で、小さいパーツを分母の数だけ作る、→ つまり分母倍する
- 分母の数で等分したパーツにそろえているので、それを分子の数で割ればそのまま答えになる。 → 分子で割る
- 結果的に、計算は「分母を掛けて」「分子で割る」事で行える → つまり、分母と分子をひっくり返して掛け算すればよい。
割る対象が1ではなくて2や3や他の数でも同じ事で、従って次のように言えるわけです:
$$A÷\frac{M}{N}=A×N÷M= A×\frac{N}{M}$$
割られる数のほうの A も分数や少数であっても構いません。考え方は同じ事です。
考え方②:掛け算と割り算は「逆演算」の関係にある
■ 掛け算と割り算は互いに逆演算の関係
■ 中学・高校的な考え方
掛け算と割り算は互いに逆演算の関係
別の考え方もあります。こちらのほうが、より「数学」でよくやる考え方です。
分数とは、そもそも割り算であるという事にまず注目します。つまり、例えば1/3を掛けるという事は、3で割る事に他ならないわけです。
分数2/3などを掛ける場合は、3で割って2倍する(2を掛ける)と解釈できます。つまり次のように書けるわけです。
$$1×\frac{2}{3}=1÷3×2$$
ここで、掛け算と割り算は、計算の順番を入れ替えても結果は同じという事は重要です。たとえば、12を2で割って3倍すると18ですが、順番を入れ替えて12を3倍してから2で割っても同じ18になるのです。
$$1×\frac{2}{3}=1÷3×2=1×2÷3$$
さて、分数の割り算ではなくて普通の割り算の時に、?÷3=2という問題で「?」の部分を出すには、3で割って2になる数を見つけるわけです。それは6ですが、これは2を3倍してあげる事で見つける事ができるのです。つまりこのような問題では、割り算の部分を掛け算にする事で「?」の部分の答えが見つかります。
また、今度は掛け算の2×?=6という問題で「?」の部分を見つけるには6を2で割って3であると計算できます。「2を掛けると6になる数を見つける」事と、「6を2で割る」事は計算としては同じ事であるわけです。
次に、分数の割り算 「1を2/3で割る」を考えましょう。 この答えを仮にPとおきましょう。
$$ 1÷\frac{2}{3}=1 ÷( 2÷3)=P$$
すると、 ?÷3=2 という問題で「逆算」して掛け算で「?」の部分を見つけたのと同じ要領で
$$1=P×\frac {2}{3} =P×(2÷3)= P×2÷3 $$
となるのです。これをよく見てみると、1 = P × 2 ÷ 3 という関係になっています。という事は、「?÷3=2」や「 2×?=6」の問題と同じ形です。もう一度逆算してあげると、P の値を表せます。
- 1 = P × 2 ÷ 3
- 1 × 3 = P × 2
- 1 × 3 ÷ 2 = P
つまり、
$$P=1 × 3 ÷ 2 =1×\frac{3}{2}$$
であるという事ですが、もともとは
$$P=1÷\frac{2}{3}$$
だったのですから、
$$1÷\frac{2}{3}= 1×\frac{3}{2} $$
という事です。
掛け算と割り算が逆の演算である関係からは、必然的に「分数による割り算」は「分子と分母を入れ替えた掛け算」になる事を意味しています。
中学・高校的な考え方
やる事は本質的に上記と同じですが、等号で結んだ関係を同じ数で掛けたり割ったりしても等号関係は保たれる事を利用する方法もあります。
$$1÷\frac{2}{3} =P$$
式の左と右の両方の側(両辺)に「2/3」を掛けます。この時、式の左側(左辺)では、 「2/3」 で割って 「2/3」 で割るのですから、その部分は何もしない(1を掛ける)のと同じ事になります。
$$1÷\frac{2}{3}× \frac{2}{3} =P × \frac{2}{3} $$
$$ 1=P × \frac{2}{3} $$
この両辺に、今度は「3/2」を掛けます。
$$ 1×\frac{3}{2}=P × \frac{2}{3} ×\frac{3}{2} =P$$
つまり結果は同じで、分数の割り算は分母分子を入れ替えた掛け算になります。
$$ 1÷\frac{2}{3} = 1×\frac{3}{2} $$
この両辺にさらに、同じ分数を掛け算する形の計算により、一般に次のように言えます。
$$\frac{A}{B}÷\frac{M}{N}= \frac{A}{B} × \frac{N}{M}=\frac{A × N}{B × M} $$
まとめ
逆演算という考え方は、数学的には非常に広い範囲で使われるので考え方としては知っておくと便利です。より一般的には、2を掛けて2で割るといったように、ある演算と逆演算の「積」は1(恒等)、つまり何もしないのと同じになるという考え方をして話を進める事があります。
しかし、単純に普通の分数の計算で「割り算はなぜひっくり返して掛け算なのか」という素朴な疑問に対する答えは前述の「1個の中に半分個は2個ある」の考え方でも良いと思います。どちらにせよ、計算結果は同じになるからです。
もう1つ、そもそもそのように計算を『定義』してしまって、その定義のもとで話を進めているのだとする考え方もあります。特に数学者という人達は具体的な『モノ』を使って説明する事を嫌う傾向にあるので、「なぜですか」と聞かれたら「定義だ」と答える事が多いでしょう。
数学という学問の中での考え方としてはそれは間違っていないのですが、『説明』としては女の子の質問に対して怒りだして暗記を強要する姉とほぼ同じである事には注意が必要かとは思います。
確かに基本的には、計算の結果が合っていれば「説明できる」必要は必ずしもないのです。計算というのは、要するに答えが合っていればよいという考え方もあるからです。しかし、子供が何か疑問に感じた場合にはきちんとそれに答えるという事も算数・数学教育では大事な事だと思います。特に、生徒からの質問に対しては、大人は誠実な気持ちで適切に対応する必要があるでしょう。
