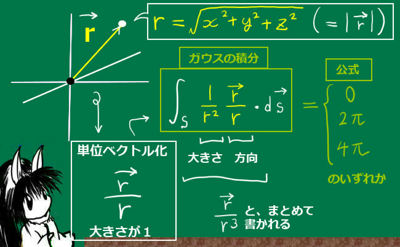
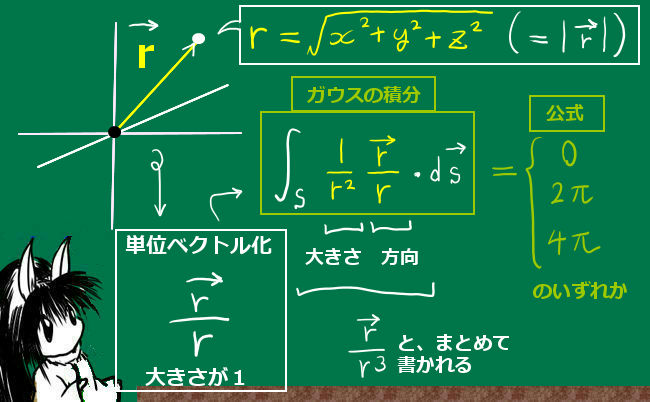
位置ベクトル\(\overrightarrow{r}\)=(x,y,z)をベクトルの大きさrで割る事により
単位ベクトル(大きさが1のベクトルを言います)にすると\(\overrightarrow{r}\)/rというベクトルとして書けます。
ベクトル\(\overrightarrow{r}\)/rをさらにr2で割ったベクトルを考えると
\(\overrightarrow{r}\)/(r3)というベクトルになり、
このベクトルに対する閉曲面上の法線面積分の事をガウスの積分と呼ぶ事があります。
この積分は、閉曲面の形状によらずに閉曲面に対する原点の位置によって3種類の値だけをとります。
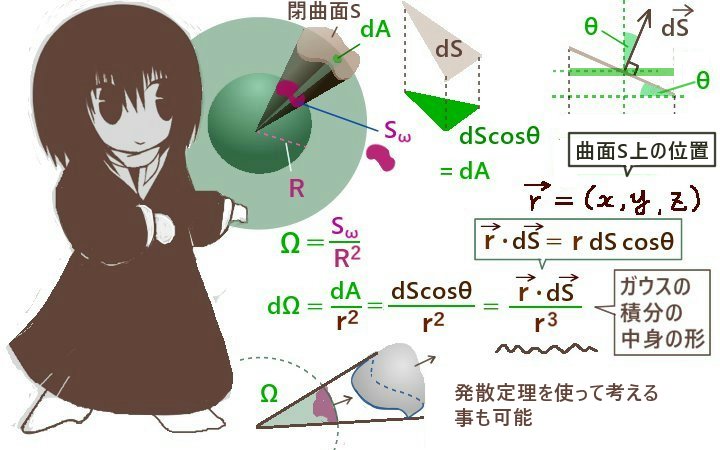
また、ガウスの積分は閉曲面に対する立体角の積分表示ともなっています。
ガウスの積分の被積分関数に入っている「距離の3乗」は、見かけ上のものであり、本質的には「距離の2乗」に大きさが反比例するベクトルである事が重要となっています。ただし、具体的な計算では「3乗」の部分が結果に影響してくる部分はあります。
■関連サイト内記事:
立体角の積分表示および球面との関係
立体角は平面角に対応する語で3次元空間的な広がりを表す量で、球の表面積を使って定義されますがその積分の形がガウスの積分と同じものになります。(ただし、ガウスの積分は閉曲面に対する積分を指し、立体角の積分表示は同じ被積分関数に対して開曲面にでも定義されます。)
ではガウスの積分も球の表面積に関連するものなのかというと実際そうであり、
後述するようにガウスの積分が取り得る値は0,2π,4πだけとなっています。
つまり積分の結果は円周率の定数倍の値だけをとるという結果です。
これらの結果は偶然にもそうなるというだけでなく、
円や球に由来して2πや4πといった数値が結果として導出されます。
その結果は物理的な考察にも使用される事があります。
ガウスの積分の被積分関数は\(\overrightarrow{r}\)/(r3)ですが、これは大きさが「r2に半比例する」ベクトルであり、向きは原点からある点までの向きそのものとなっています。そのようなベクトルは物理的な力や場を表すものとして存在し、具体的には静電気力や万有引力、一部の磁気力などが挙げられます。代表的なものは電場に関するガウスの法則であると言えます。
そして物理での考察で使用する時にも「球面」は重要な要素となります。
ガウスの積分の内容
ガウスの積分とは具体的には次のようなものです。
\(\overrightarrow{r}=(x,y,z)\)および
\(r=|\overrightarrow{r}|=\sqrt{x^2+y^2+z^2}\) のもとで、
閉曲面Sに対する次の法線面積分をガウスの積分と呼びます。
$$\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}$$
この時に閉曲面Sは任意の形状ですが、
「どのような閉曲面に対してでも、ガウスの積分が取り得る値は3つしかない」
事が知られています。
原点と閉曲面の位置関係によって結果が分かれます。
- 原点が閉曲面Sの「外側」にある場合: $$\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=0$$
- 原点が閉曲面Sの「曲面上」にある場合: $$\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=2\pi$$
- 原点が閉曲面Sの「内側」にある場合: $$\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=4\pi$$
2番目(閉曲面上)の式は極限値として考える必要があり、
3番目の式もそのように考える事もできます。
物理学では値が無限大になってしまう点を特別扱いできるデルタ関数を使ってガウスの積分により表現される内容を表す事もあります。
あるいはガウスの積分は閉曲面に対しての立体角と同一視できるので立体角の文脈で話を進める事もあります。
ガウスの積分の計算および証明
次の3つの場合分けがあります。
この証明にはガウスの発散定理の結果と、ベクトル場に関する発散(div)の計算を使います。
ここで言う「発散」とは極限における「収束と無限大への発散」の意味ではなく、物理的には「湧き出し」の意味を持ち数式的には偏微分で定義されるスカラー量を作る演算およびその結果を指します。
①原点が閉曲面の「外側」にある場合
対象のベクトル場の発散 \(\mathrm{div}\frac{\Large \overrightarrow{r}}{\Large r^3}\)を直接計算すると、
実は必ず0になるという結果が得られます。
$$公式:\mathrm{div}\left(\frac{\overrightarrow{r}}{ r^3}\right)=0$$
この式は、より一般的な公式である\(\mathrm{div}\left(r^n\overrightarrow{r}\right)=(n+3)r^n\) の結果でもあります。
すなわち、n=3の時は結果が0となるわけで、div\(\overrightarrow{r}\)/(r3)を表しています。
次に、ガウスの発散定理によればベクトル場の法線面積分は
「ベクトル場の発散を被積分関数とした体積積分」によって表せます。
ここで\(\mathrm{div}\frac{\Large \overrightarrow{r}}{\Large r^3}\)の体積積分を考えるとすれば
「被積分関数が定数関数でしかも値は0」なので、考えている領域での積分の結果も0です。
ただし、\(\overrightarrow{r}\)/(r3)は原点で定義できない関数である事に注意する必要もあります。
しかしまずは「原点が閉曲面の外側にある場合」を考えているので、
この場合には閉曲面の領域に定義できない点は含まれません。
そのため、発散定理により次のように書けます。
$$\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_V\mathrm{div}\left(\frac{\overrightarrow{r}}{r^3}\right)dv【∵ガウスの発散定理】$$
$$=\int_V\hspace{3pt}0\hspace{3pt}dv=0$$

②原点が閉曲面の「曲面上」にある場合
原点が閉曲面上にある場合でも、
ベクトル場の発散 div \(\overrightarrow{r}\)/(r3)を計算すると0になるという事は同じです。
しかし\(\overrightarrow{r}\)/(r3)は原点で定義できず、かつ原点が考えている閉曲面上にある場合には
「積分したい領域内で被積分関数が定義できない点を含む」
という事を意味します。
従って法線面積分を考える閉曲面Sについて、通常の閉曲面とは違うものを考える必要があります。
具体的には、閉曲面から原点を除いたものを領域として考える必要があります。
ただし、1点だけを除くという考え方だと積分の計算がうまくいかないので、もとの閉曲面から原点付近のわずかな領域を除いた部分を改めて閉曲面Sとします。
さらにこの場合では、原点を含む「面だけ除く」事もできないので
体積を持った領域ごと除く事になります。
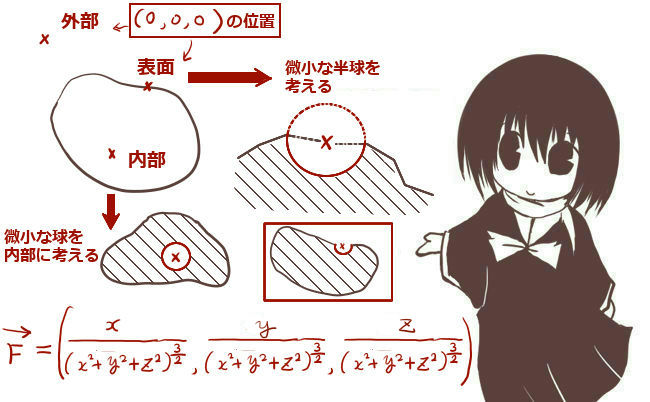
そして、除く領域の形状は「半球」とする必要があります。これには理由が2つあります。
- 球面であれば曲面に対する法線とベクトル場\(\overrightarrow{r}\)/(r3)の方向が平行になるので、法線面積分を直接計算できる利点があります。
- 発散定理により領域内でベクトル場の発散が0であれば「1つの閉曲面を構成する2つの開曲面の法線面積分はそれぞれ等しい事」が示されます。そのため、一番計算しやすい領域で計算すれば十分という事になるので球面を考えます。
上手にきれいな半球を繰り抜けるかどうかは、閉曲面を多面体に近似することで可能になります。法線面積分が成立するの十分細かい分割の多面体で考えた時に、平面状の微小領域よりも半径が小さい球を考えればそこで半球状にくり抜く事ができます。
原点を中心とする微小な半径ρの半球S0を考えて、S0は外縁となっている円周部分(球を2つに割った所の部分)を閉曲面Sと共有するとします。
また、閉曲面S上から半球S0で囲まれる領域を除いた部分をS1とします。この時に曲面S1は開曲面であり、閉曲面Sに「穴」が開いて形状をしています。
ここで半球S0と開曲面S1を合わせた領域は「原点が外部にある閉曲面」となっています。(もとの閉曲面Sと同一ではありません。)そこで半球S0と開曲面S1を合わせた閉曲面をS1∪ S0とおきます。【「∪」は和集合の記号です。】
この時に、原点を除いて\(\mathrm{div}\frac{\Large \overrightarrow{r}}{\Large r^3}=0\)であり、S1∪ S0は原点を含まない事から発散定理を適用すると法線面積分の値は0です。S1∪ S0の内部の領域をV1として、次の計算ができます。
$$\int_{S1\hspace{1pt}U\hspace{1pt}S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{V1}\mathrm{div}\left(\frac{\overrightarrow{r}}{r^3}\right)dv=0により、$$
$$\int_{S1}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}-\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=0\Leftrightarrow\int_{S1}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}$$
つまり半球S0の法線面積分と開曲面S1の法線面積分の値は一致します。
そして結論から言うと半球S0のほうの積分の値は具体的に計算できます。
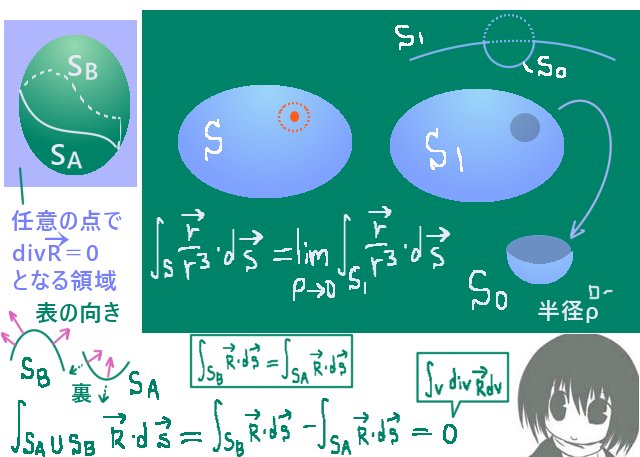
半球S0は原点を中心とした半径ρの半球なので、
S0上でベクトル場\(\overrightarrow{r}\)/(r3)の大きさはどこの点でも等しく1/(ρ2)です。
方向については各点で球面に垂直で外側向きなので法線との内積は1となり、
法線面積分は定数関数に対する面積分となります。
この時には面積要素を分割して合計して定数倍を考える事になりますが、面積要素を十分細かい分割のもとで合計した極限値は「表面積」に他ならないので面積分は表面積の計算を意味します。
すると考えている領域が半球なので、その表面積は\(2\pi\rho^2\)です。
これによって法線面積分の結果を出せる事になります。
$$\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\frac{1}{\rho^2}\int_{S0}ds=\frac{1}{\rho^2}\cdot 2\pi\rho^2=2\pi$$
結果を見ると「半径ρ」が消えているので、
実は半径の大きさに関わらず積分の値は一定であるという事になります。
そのため、穴の開いた開曲面S1の法線面積分は
半球S0の法線面積分に等しいという事だったので次のように表せます。
$$\int_{S1}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=2\pi$$
半球S0の法線面積分の値は半径ρによらず同じなので、
上式はρ→0の極限でも成立して次のように書けます。
S0の法線面線積分の符号を変えているのは
「原点を中心に半球を単独で考察した時」と閉曲面S1を構成する時とで
考えた時の「外側への向き」が逆になるためです。
結果的に引き算する形となります。
$$\lim_{\rho\to 0}\int_{S1}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\lim_{\rho\to 0}\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=2\pi$$
他方でもとの閉曲面Sに対する法線面積分を
穴が開いた曲面S1の法線面積分に対して半球S0の半径が0になる極限値で表すもの
とすると次のようになります。
$$\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\lim_{\rho\to 0}\int_{S1}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=2\pi$$
よって、原点が閉曲面上にある場合のガウス積分値は2πであるという事が言えます。
考えてきた閉曲面を整理すると次のようになります。
| 曲面 | 原点との位置関係 | 積分計算での意味 |
| S | 閉曲面 原点が閉曲面上にある | 被蹟分関数が定義できない点を含むので 積分はそこを除外して極限値として計算 |
| S0 | 開曲面で、原点を内部に含む。 (中心が原点で半径ρ) | 法線面積分の値は2πで、 半径ρに関わらず同一の値 |
| S1 | 開曲面で穴が開いている | SからS0の内部を除いた領域 S1の法線面積分はS0の半径ρ→0の極限で Sの法線面積分になると考える |
③原点が閉曲面の「内側」にある場合
閉曲面の内部に原点がある場合にも、閉曲面上に原点がある場合と同じ問題が発生します。ただしこの場合は閉曲面内部で体積積分を行う時に除いて考えるべき点が生じる事になります。
閉曲面Sの内部から「原点を囲む微小な球をくり抜いて除いた」領域を考えます。
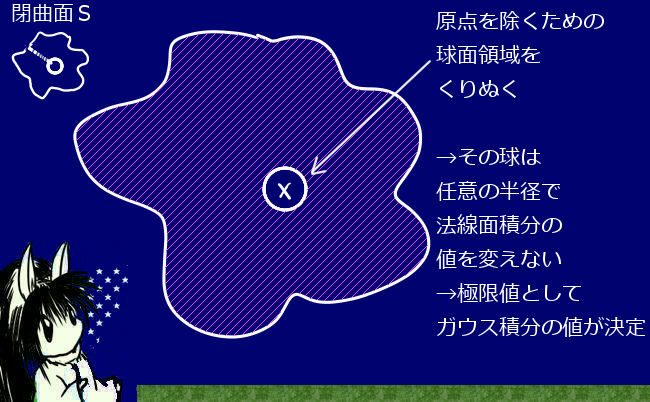
原点を含む領域を球状に除いて、球の半径を0に近づけた時の極限値として
ガウスの積分の値を計算します。
原点が閉曲面上にある時と類似の計算により、
閉曲面の内部から除いた球面上での法線面積分は球の半径ρにかかわらず一定値になります。
球の表面積4πρ2をρ2で割る計算となり、結果は\(4\pi\)です。
より具体的には閉曲面Sと、その内部で原点を中心とする小さい半径ρの球S0を考えてSとS0を接続するてきとうな曲面を考えます。(その曲面上では法線面積分は表と裏の両方で計算する事になり、プラスとマイナスの値が打ち消して0になります。)そのようにしてできる全体の閉曲面をSUとします。
この閉曲面SUは原点を含まない閉曲面であり、
内部の領域VUにおける任意の点で\(\mathrm{div}\frac{\Large \overrightarrow{r}}{\Large r^3}=0\)なので発散定理により法線面積分の値は0です。
よって表と裏の関係による符号に注意して、
閉曲面Sと球S0の法線面積分の値は同じです。この場合は球S0の半径ρ→0の極限を考えなくても結果の式が出ますが極限を考えても値は同じになります。(内部の領域まで元の領域に近付けるなら極限を考える必要があります。)
$$\int_{SU}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{VU}\mathrm{div}\left(\frac{\overrightarrow{r}}{r^3}\right)dv=0により、$$
$$\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}-\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=0\Leftrightarrow\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}$$
$$(任意の\rho で)\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=4\pi なので、$$
$$\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=4\pi$$
球面S0の法線面積分は球の外側を表としていて、それは閉曲面SUから見ると裏側になるので閉曲面SUの法線面積分の構成要素としては球面S0の法線面積分はマイナス符号をつける事になります。
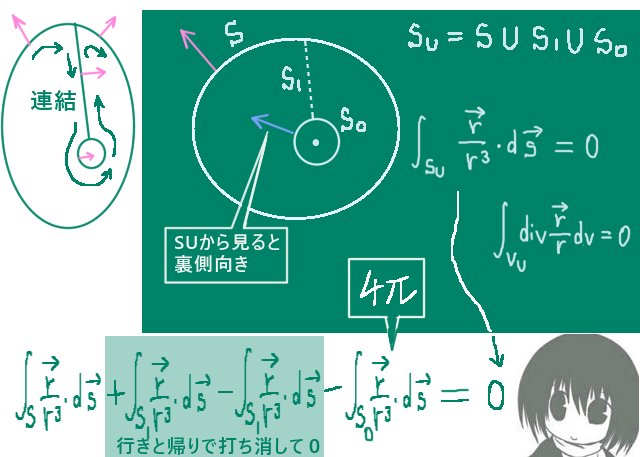
計算の導出過程を見ると、原点が「閉曲面内にある時」と「閉曲面上にある時」のガウスの積分の値の2倍の差は「球」と「半球」の表面積の違いを意味しているという考察もできます。
| 原点と閉曲面の位置関係 | ガウスの積分の値 | くり抜いて除外する領域の形状 |
| 閉曲面の外側 | 0 | 特に無し |
| 閉曲面上 | \(2\pi\) | 半球 |
| 閉曲面の内側 | \(4\pi\) | 球 |