円周率は無理数です。つまり、整数の比(分数)では表せない実数であるという事です。
その証明方法は1つではありませんが、一般的な2つの方法は次の通りです。
- 背理法と部分積分で示す方法:円周率が有理数であると仮定すると矛盾が生じる。
- 連分数とライプニッツ級数を使う方法:円周率が無限連分数となる事を示す。
2番目の方法は計算自体は比較的簡単ですが、まず「ライプニッツ級数」「無限連分数」といったものが何なのかという話にもなるので、その意味では分かりにくいかもしれません。
そのため、背理法のほうを先に述べます。背理法での一般的な証明では計算は少しごちゃごちゃしますが、使うものは高校数学の知識で済むのです。
背理法と部分積分による証明
この背理法による証明は、円周率は「有理数ではないでしょう」という予想はあらかじめつけたうえで、矛盾が生じてしまうような関数を敢えて探してくるという方法になります。
まず、円周率そのものを式でどう表すかという問題があります。これには、ライプニッツ級数やマチンの公式をはじめ様々なものがありますが、背理法で示す場合にはむしろ三角関数を使ったほうが比較的簡単である事が知られています。
f(x)sinxで表される関数の定積分の、部分積分を考えます。
$$\int_0^{\pi}f(x)\sin xdx\hspace{10pt}の部分積分を考えます。$$
$$\int_0^{\pi}f(x)\sin xdx=-\left[f(x)\cos x\right]_0^{\pi}+\int_0^{\pi}f^{\prime}(x)\cos xdx$$
$$=-\left[f(x)\cos x\right]_0^{\pi}+\left[f^{\prime}(x)\sin x\right]_0^{\pi}-\int_0^{\pi}f^{\prime\prime}(x)\sin xdx$$
$$=-\left[f(x)\cos x\right]_0^{\pi}+\left[f^{\prime}(x)\sin x\right]_0^{\pi}+\left[f^{\prime\prime}(x)\cos x\right]_0^{\pi}-\int_0^{\pi}f^{\prime\prime\prime}(x)\cos xdx=\cdots$$
という感じで、これは延々と続いていくタイプの部分積分です。ここで、sinxに0と円周率を代入する箇所はゼロになる事に注意し、f(n)(\(\pi\))+f(n)(0)=Cnとおきます。【f(n)(x)はf(x)のn階導関数です。】
$$-\left[f^{(2n)}(x)\cos x\right]_0^{\pi}=f^{(2n)}(\pi)+f^{(2n)}(0)=C_{2n}$$
$$\left[f^{(2n+1)}(x)\sin x\right]_0^{\pi}=0$$
すると、上記部分積分はてきとうなところで部分積分を止めて次のように表せます:
$$\int_0^{\pi}f(x)\sin xdx=C_0-C_2+C_4-C_6+\cdots\pm\int_0^{\pi}f^{(n)}(x)\sin xdx$$
今、f(x)の形は特に指定しておらず、円周率がどんな値であるかに関わらずこの式は成立します。

ここで、f(x)がn次の多項式の形で定数項が特定の値のもの、例えばf(x)=axnなどといったものであれば、有限回の微分操作で0になり、しかも上記の部分積分の途中の項で円周率が直接式に出てきます。
f(x)がそのような条件を満たす多項式であるとして、まず、有限回の微分操作でf(n+1)(x)=0になるので、
上記の部分積分では最後の積分の形の項が消えて次のように有限項の和として書けます。
$$\int_0^{\pi}f(x)\sin xdx=C_0-C_2+C_4-C_6+\cdots\pm C_{2n}$$
このCnは、上でも定義したようにf(n)(\(\pi\))+f(n)(0)=Cnとおいたものです。
ここで、各項はCm=f(m)(\(\pi\))+f(m)(0)=a\(\pi\)nのように表されるので、円周率のベキ乗に係数を掛けたものの和になっています。さらに、aをてきとうな有理数に選べば、円周率が有理数であると仮定した時に【これが誤りであるわけですが】もとの定積分が整数となるようにできます。
例えばf(x)=axnとして、pとqを自然数として\(\pi\)=p/qとおいた時に、aをqnの倍数にとってa=mqnのようにすれば\(\pi\)na=mpnとなり、整数となるわけです。
【※円周率は3.14・・・という正の数である事は確定しているとしています。】
後述しますがそのようにするためのaの値はもっと小さい有理数でもよく、それが証明の根拠になります。
ところでもとの定積分は、正弦関数の絶対値が1以下なので、積分区間でf(x)が正の数であれば次の不等式が成立します。
$$0<\int_0^{\pi}f(x)\sin xdx≦\int_0^{\pi}f(x)dx$$
という事は、もし何らかの関数f(x)でこの定積分の値が「1未満」になるものが存在すれば、もとの定積分は0より大きく1未満という事になって自然数ではあり得ないという事になります。
この事との「矛盾」がこの背理法での証明で使われます。
【こちら側の事実は円周率が有理数・無理数であるかに関わらず常に成立する正しい関係式です。】
問題の定積分をC0-C2+C4-・・・±C2nの形で表すところに戻って、
f(x)としてできるだけ「小さい値」をとるような関数が何かないかと考えます。
【多分あるはずだという予測のもとでそう考えるわけです。】
結論を言いますと、x=0とx=\(\pi\) でゼロの値をとるような2n次の多項式f(x)=axn(\(\pi\)-x)nを考えるとうまくいきます。このようなf(x)について、f(0)=0かつf(\(\pi\))=0です。
定義域を [0,\(\pi\)]とすると、a>0であればこの関数f(x)はプラスの値です。
ここでf(x)のk階導関数について、1≦k≦n-1のとき、積の微分公式を考えれば、f(k)(x)はx(\(\pi\)-x)を因数に持つ事が分かります。【因数分解できるという事です。】
という事は、その時にはf(k)(0)=0かつf(k)(\(\pi\))=0という事になります。
Ckについて言えば、Ck=f(k)(\(\pi\))+f(k)(0)でしたから、C0=C2=C4=・・・=Cn-2=0となるという事です。次に、n≦k≦2nの時はどうかというと、この時にはx(\(\pi\)-x)の形の項で全体を因数分解はできません。しかし、axn(\(\pi\)-x)nの形の関数をn回以上微分しているので式全体がn!を因数に持ちます。
何らかのn次以下の多項式で、全体がn!を因数に持つという事になります。
よってこの時、
C0-C2+C4-・・・±C2n=±(C2m-C2m+2+C2m+4-・・・±C2n)=n!ag(\(\pi\))という形になり
ここでのg(\(\pi\))の部分は、n次以下の整数係数の多項式に円周率を代入した形です。
【n=2mとおいています。符号が入り乱れますがここであまり本質的ではありません。】
$$g(\pi)=b_n\pi^n+b_{n-1}\pi^{n-1}+\cdots+b_2\pi^2+b_1\pi+b_0\hspace{10pt}【係数b_jは全て整数】$$
$$n!ag(\pi)=n!a(b_n\pi^n+b_{n-1}\pi^{n-1}+\cdots+b_2\pi^2+b_1\pi+b_0)$$
さて、とすると、f(x)=axn(\(\pi\)-x)nにおいて、
「自然数pとqを使って \(\pi\)=p/q で表せるという(誤った)仮定」をすると、
C0-C2+C4-・・・±C2n全体を整数にするためには、aをqn/n!のようにした場合でも可能です。
この時の分母のn!の階乗がなくてもそれは成立しますが、できるだけ小さい値の関数を考える時に、少なくともここまで小さい物を考える事が確かに可能だという事です。
ところが、f(x)=(qn/n!)xn(\(\pi\)-x)n であるとすると、0≦x≦\(\pi\)においてはxn(\(\pi\)-x)n≦\(\pi\)n・\(\pi\)n=\(\pi\)2nとなるのでf(x)≦\(\pi\)2nqn/n!
という事は、問題の定積分の不等式に再度戻ると次のようになります。
$$0<\int_0^{\pi}f(x)\sin xdx≦\int_0^{\pi}f(x)dx≦\int_0^{\pi}\frac{\pi^{2n}q^n}{n!}dx=\frac{\pi^{2n+1}q^n}{n!}$$
この最後のところの式は、テイラー展開の剰余項問題のところでも出てくるような形の式ですが、nをじゅうぶん大きくすると極限値を0にできるものであり、1未満になるようなnも確かに存在できます。
【ここでのqがどのような自然数でも、\(\pi\)2nqn/n!<1になるような自然数nが存在するという事です。また、ここでのnは、てきとうなところで部分積分を打ち切った自然数であり任意にとれるので「じゅうぶん大きいn」を考えてよいという事です。】
つまり結果は次式です。
$$0<\int_0^{\pi}f(x)\sin xdx≦\int_0^{\pi}f(x)dx≦\int_0^{\pi}\frac{\pi^{2n}q^n}{n!}dx=\frac{\pi^{2n+1}q^n}{n!}<1となる自然数nが存在$$
$$かつ、\int_0^{\pi}f(x)\sin xdx=C_0-C_2+C_4-C_6+\cdots\pm C_{2n}\in \mathbb{Z}【整数】$$
これは「矛盾」なので、円周率は有理数ではあり得ない、という事です。
★この「0より大きく1より小さい整数は存在しない」という事を利用する証明方法は、ある数が無理数である事や超越数である事を示す時によく使われるものです。また、問題となっている数と整数を関連付けるために微積分(特に微分)を使うのも比較的よくある手法です。
一体どこがおかしくて矛盾が出たのかというと、\(\pi\)=p/q とした時に「pとqは自然数」としたところがおかしい事になります。その仮定を設けずに単に\(\pi\)=p/q とおいてf(x)=(qn/n!)xn(\(\pi\)-x)nとする事【そのようなf(x)を考える事】自体には問題はありません。
そのf(x)のもとで問題の定積分を部分積分したものについてC0-C2+C4-・・・±C2n<1となる【そのようになるようなf(x)が存在する】という事自体も正しい式で、「そのような制限が必ず付くので、円周率を有理数とする事はできない」というようにも言えます。
証明において、どこからどこまでが「もともと正しい関係式」であって、どこからが「誤った仮定により導出される間違った式」なのかを整理すると見通しはよくなるでしょう。
ここでは説明のために長く文章も書きましたが、やり方をふまえて式だけ書いていくと、やっている事自体は結構簡単である事が分かると思います。
一番難しいのは、「問題の定積分が0より大きく1未満になり、かつ誤った仮定をするとその定積分が整数になってしまうという関数」を「(自力で)見つける」事だと思います。しかし一般的には、事実としてこうなる事を知っておけばそれでじゅうぶんでしょう。
連分数とライプニッツ級数による証明
もう1つの証明方法は、円周率を連分数で表すと、有限の連分数にならず、無限連分数になってしまう事から「無理数である」と判定するものです。
しかし、まず「連分数」とは何かという話になります。ここでごく簡単に述べると、次のように分母の中に「整数+分数【有理数】」の形を作っていき数を表示するものです。
$$ b_0+ \frac{a_1} {b_1+\Large{\frac{a_2} {b_2+\frac{a_3} {b_3+\frac{a_4} {\Large{\frac{\cdots}{b_{n-1}+\frac{a_n}{b_n}}} } } } }} $$
これは見慣れない人も多いと思います。実際、物理などへの応用では基本的には使わず、数学に特有のものでしかも数学の中でも限られた分野でたまに使うというものです。
特定の有理数を連分数で表す時、その中の数列{an}と{bn}は有限で終わります。他方、無理数であると無限に続いてしまうというのが証明の考え方です。
考え方としては「ある実数が有理数」⇒「連分数が有限で終わる」が正しいので、「ある実数を表す連分数が有限で終わらない」⇒「その実数は有理数ではない(=無理数である)」というものです。
【※ある連分数が無理数に収束するための条件は、じつのところもう少し複雑です。】
次に、円周率を何らかの形で分数として表す手段が必要です。ここでの証明では、ライプニッツ級数を使うと比較的簡単です。しかしこの公式がどのように出てくるのかという問題もありますが、ここでは結果のみを使います。
【ライプニッツ級数は、扇形の面積を少し工夫した積分で出す方法や、逆正接関数のマクローリン展開などによって導出できます。】
$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots$$
これを連分数にしてみようというわけです。有限の数列の和を連分数にするにはじつは公式があって、結論を数列の隣り合う項の比を考えるとうまくいきます。
簡単のため、まず3項目までやってみて、次に一般の場合を記します。
$$1-\frac{1}{3}+\frac{1}{5}=\frac{1}{1+\Large{\frac{\frac{1}{3}}{\frac{2}{3}+\frac{3}{5}\cdot\frac{5}{2}}}}=\frac{1}{1+\Large{\frac{1}{2+\frac{3^2}{2}}}}$$
これは、じつは次のように数列を計算しているのです。
a1=1【初項】,b1=1【必ず1】,
a2=-(-1/3)/1=1/3【-第2項/第1項】,
b2=1-a2=2/3,
a3=-(1/5)/(-1/3)=3/5【-第3項/第2項】,
b3=1-a3=2/5
同じ具合に計算して、分母を上手に整理すると、第n項までの結果は次のようになります。
$$ \frac{1} {1+\Large{\frac{1} {2+\frac{3^2} {2+\frac{5^2} {\Large{\frac{\cdots}{2+\frac{(2n-3)^2}{2}}} } } } }} $$
このようになるのは、次のように計算できるためです。
am=-{-1/(2m-1)}/{1/(2m-3)}=(2m-3)/(2m-1)
【もしくは-{1/(2m-1)}{-1/(2m-3)}=(2m-3)/(2m-1)】
bm=1-am=2/(2m-1)となり、
m≧2の時、
bm+am+1/(・・・)=2/(2m-1)+(2m-1)/{(2m-3)(・・・)}
=2+(2m-1)2/{(2m-3)(2m-1)(・・・)}
すると、nを増やしていくとこの連分数は無限に続いていく事になります。そのため、円周率は無理数であると判定されるという具合です。
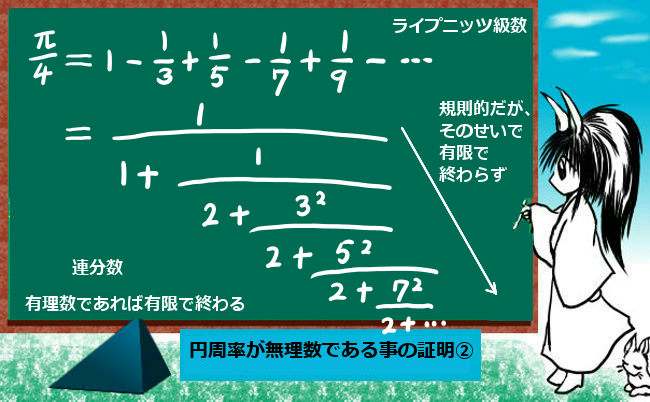
このように、連分数が「規則正しく」続いていくと、かえってnを増やすごとに延々と続いて終わらないので特定の収束する無限級数が「無理数」であるという事を意味するわけです。
円周率だけでなく、2の平方根や自然対数の底eなどが無理数である事を見るのにも、じつはこの連分数の方法を使う事が可能です。
ここで使っているものは、分数計算とちょっとした数列の計算だけなので、計算自体は前述の背理法の場合よりもずっと簡単だと思います。しかしいかんせん、この連分数というものの表記も理屈も、結構分かりにくいものだと思います。また、ライプニッツ級数で円周率を表せる事を前提にしていますから、その事が確かに成立する事を納得していないと、ここでの証明も少々「腑に落ちない」ものだと思います。
いずれにしても、これらのような形で円周率は確かに「無理数である」という事が言えるという事です。
