波を表す具体的な形として最も基本的な「正弦波」は関数としては三角関数の正弦関数 sinθですが、波動を表す関数として考える時の変数としては位置座標と時間の両方を考えるのが普通です。
「振動」も波動に関連が特に深い物理現象であり、波動においても個々の位置では振動が起きているとみなせる事もあります。ただしここではバネの振動現象などは除いて、特に波動のほうに注目して見て行きます。
水面の波、あるいは数学では三角関数の sinθのグラフのイメージで上下方向の振動(グラフだとy方向)を特に「変位」と呼ぶ事あり、ここでもその言い方を使います。横に進んでいく方向(グラフだとx軸方向)を波が「進行」する方向と呼ぶ事にします。
物理的な「波」の種類
波動は基本的には何かの物質が個々の位置で時間変化により振動していて、その振動が周囲にも伝わっていく事を指します。その振動して波を構成する物質は媒質(「ばいしつ」)と呼ばれます。例えば海の潮の満ち引きの「波」の媒質は水であり、音の場合は基本的には媒質は空気で、水中やそれ以外の物質でも音は伝わるので色々な物質が媒質になり得ます。
他方で「媒質が無くても媒質による波と同じように振る舞うもの」は物理上、普通は「波」として扱われてそのようにも呼ばれる事が一般的です。例えば光(および電磁波)は、実は何かの媒質が直接的に振動しているわけでは無い事が知られています。
また同じく、一般的にミクロのスケールでの量子力学的な「波」は定量的には波動と同じように振る舞うという事を意味し、何かの媒質が直接的に振動しているわけではないという考え方がなされます。(光も、より詳しく見る場合には量子力学的に解析されます。)
他方で正弦波に近い形の電圧である交流電圧は、人工的に起電力をそのような形で発生させ続ける事によって波と同じ関数形として扱うという類のものです。
しかしいずれにしても、数式的に波の形として扱える物理量には、媒質の振動による波動の用語や考え方の多くを適用できます。特に光および電磁波に関しては普通に代表的な波動の現象の1つとして捉えられる事が一般的です。
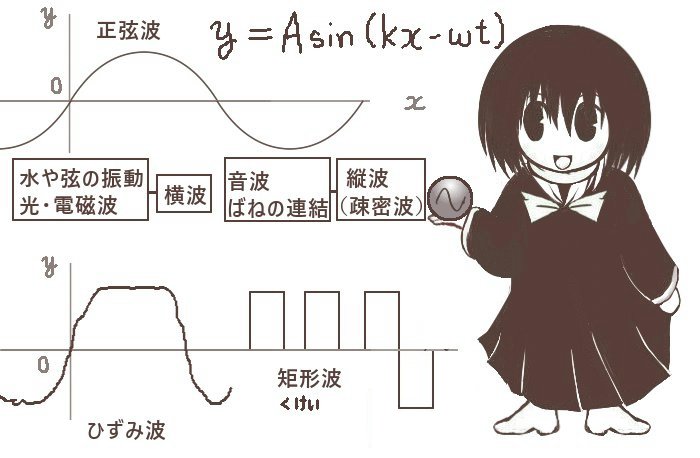
実際に目で見える波の形や、物理量をグラフとして描いた時の形は波形と呼ばれます。
正弦波の波形はそのまま正弦関数のグラフの形ですが、波形は一般的には他の形状もあります。
例えばグラフ上で長方形状になる波形は
方形波あるいは矩形波【矩形:「くけい」長方形の事。矩とは直角の意味。】などと呼ばれます。
また、一般的に正弦波の波形が微妙に歪んでいたり台形状や三角形状の波形になっている波を総称してひずみ波と呼ぶ事もあり、矩形波等を含めてそのように呼ぶ事もあります。
数学的には、実は正弦波以外の波は周期関数でないものも含めて
「振動数が異なる複数の正弦波の合計(重ね合わせ)」として表現できます。
そのように解析した場合には波を構成する正弦波のうち振動数が最も小さいものを基本波と呼び、残りの物を高調波と呼ぶ事があります。
波動は進行方向に対する振動の向きの方向によっても分類され、一般的に横波と縦波の2つに大別されます。(ただし、数式的に「波として扱える」だけの場合はどちらにも含めない事もあります。)
正弦関数のグラフの形が実際の波の波形として観察できるようなものは「横波」のほうで、水面や弦を伝わる一般的なイメージの波や、光および電磁波は横波に相当します。
横波は、より詳しくは「各位置での振動が波の進行方向に対して垂直である波」を指します。
他方で、ばねを多数連結させた構造や、音波などは「縦波」です。これは、各位置での振動の向きが波の進行方向に対して平行(そして重なっている)である事を意味していて、媒質の密度が大きくなったり小さくなったりを繰り返すので「疎密波」とも呼ばれます。
数式的には縦波も横波と同様に扱う事ができます。
以下では、比較的イメージしやすい横波を想定して説明をしていきます。
また、まずは基本的な考え方となる「進行方向が1次元の波」を正弦波として扱います。(進行方向が1つの軸方向という意味で1次元であり、振動による「変位」も含めれば2次元です。)
波の進行が平面や空間で行われる場合には波の振動の変位が一定となっている波面を想定し、
波面が平面状である平面波や波面が球面状(球対象)である球面波をなどを考えます。
また、平面波において平面電磁波のように波(として扱える物理量)の変位の向きが平面の特定の方向であるものは偏波とも呼ばれます。(光の場合は特に「偏光」とも言います。)
偏波における波の振動の変位の方向が変化しないものは特に直線偏波と呼ばれ、
振動の変位の方向が平面内で変化する場合の偏波を回転偏波と呼ばれる事があります。
さらに細かく見ると回転偏波には特定の規則性を持った円偏波などがあります。
波を構成する物理量
規則的にうねる波を正弦関数で表す事を考える時に、
「波と言ってもどのような波なのか」を表す物理量として次のものがあります。
便宜上ここでは、1回転して元の状態に戻る事をさして「1サイクル」と表現しておきます。
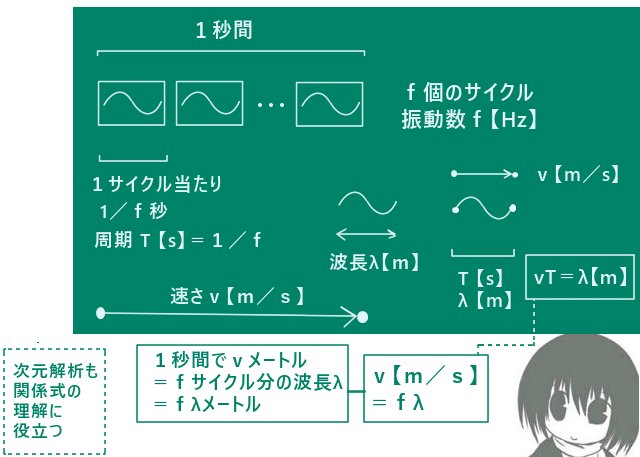
- 周期:何秒で正弦波が1サイクルするのか
- 波長:波形で見た時に1サイクルが何メートルあるか(時刻は固定して見た時)
- 振動数:1秒間で考えた時に何サイクルしているのか。周波数とも言います。
- 速さ:波形が1秒当たり何メートル進行していくのか。(時間を進めながら位置も見る。)
- 振幅:波の高さが0から最大値まで何メートルあるのか。
正弦関数 sinθの変数は「角度」です。しかし位置や時刻などの物理量は普通はπの倍数で表しませんから、それを補正して正弦関数に反映されるようにします。
- 波数:考えている位置や距離が「波長の何倍か」を表す係数です。
- 角周波数:「1秒当たり角度は何ラジアン進むのか」を表します。角振動数とも言います。回転運動等で使う「角速度」と数式的には同じです。
- 位相:sinθのθの部分を合成関数になっている場合も含めて特に指す量。
基本的に弧度法(2πを360°とする)で表します。「引数」と呼ばれる事もあります。
位置座標や時刻は、波数や角周波数を乗じる事によって位相としての量に変換されます。
「2つの波は位相がπずれている」などと言う場合には角度全体で言うと sinθとsin(θ+π)の関係である事を表します。普通は位相は0から2πまたは-2πから2πまでの値とします。
また、波のy座標方向の値をここでは「変位」と呼んでおきます。
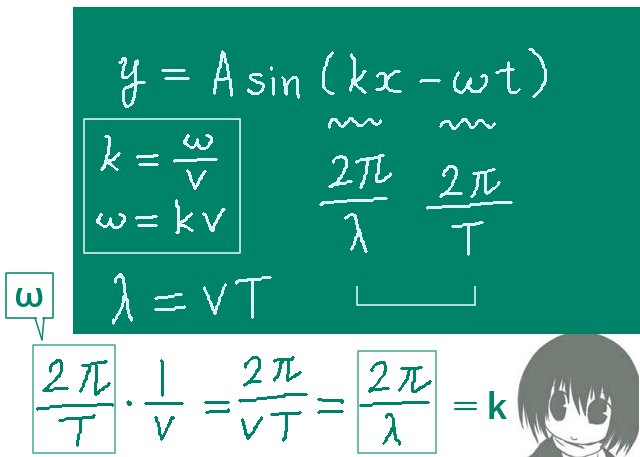
これらに対して多く使われる記号や関係式を整理すると次のようになります。
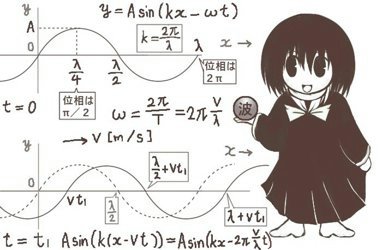
波動を表す正弦波は A sin (kx―ωt) を基本形として表されます。【あるいはA sin (ωt―kx)】
A:振幅 k:波数 x:位置座標 ω:角周波数 t;時刻 kx―ωt:位相
| 物理量 | 記号 | 関係式 | 備考 | 単位 |
| 周期 | T | T=1/f=λ/v | period, time period | 【s】秒 |
| 波長 | λ | λ=vT=v/f | wave length | 【m】メートル |
| 振動数 | f | f=1/T=v/λ | frequency 別名:周波数 | 【Hz】ヘルツ |
| 速さ | v | v=λ/T=λf | wave speed 波の進行の速さ | 【m/s】 |
| 振幅 | 色々 | 0からの最大値 | amplitude | 【m】メートル |
| 波数 | k | k=2π/λ | wave number 1波長で2π | 【rad/m】 |
| 角周波数 | ω | ω=2πf=2π/T ω=kv | angular frequency 別名:角振動数 | 【rad/s】 |
単位については「ラジアン」の代わりに無単位とする事もあります。
v は速度(velocity) から。通常は速度ベクトルの大きさを「速さ」と呼びます。
振幅の記号は用途ごとに変えるのが普通です。(一般論ではAが多い。)
光に対しては振動数をν(ニュー)で表す事もあり、光の速さはcで表します。
波動を正弦波として考える時には基本的に角度を弧度法で扱います。すなわち円周率πの何倍であるかで正弦関数の変数を表して、2π で1サイクルして0の時と同じ関数の値に戻ると考えます。
物体の位置関係や傾き具合を三角比として表すような場合であれば、
物理現象を表す時でも「斜面に対して45°の傾きなので cos45°を乗じて・・」といった表現でも全く支障は無いと言えます。
しかし波動や振動においては周期関数としての三角関数を扱う必要がある事に加えて、
微分や積分を行う観点からも三角関数の位相部分を弧度法で扱っていく必要があります。
例えばy=A sin (kx―ωt)をxやωで偏微分すると
合成関数の微分(ここでは1変数の時と同じ)となるので
(∂y/∂x)=kA cos (kx―ωt)
(∂y/∂t)=-ωA cos (kx―ωt)
のような計算になりますが、
もし位相の部分を度数法で表していたら同じ計算にはなりません。
そのため物理学の中でも特に波動や振動を扱う時には、三角関数の角度は度数法ではなく弧度法で統一的に表す事が理論的にも重要であると言えるわけです。
※合成関数に対する偏微分の一般式は、ここでは不要ですが項が1変数の時よりも増えます。
周期と振動数の関係
振動数の単位には普通【Hz】(「ヘルツ」)を使いますが、
これは無単位(正確には「1」)を秒で割った【/s】にも等しいものです。
周期と振動数の関係T=1/fについては、
例えば1秒間に50サイクルの振動を繰り返す場合には
1サイクルあたり0.02秒という事になり、
これは50【Hz】の振動数に対して
1/50=0.02【s】という計算をしているわけです。
T=1/fという事はTf=1が必ず成立する事を意味しますが、
Tは「1サイクルするのにT秒かかる」事を意味し、
fは「1秒間にfサイクルする」事を表すので
要するにTf=1は「T秒間で1サイクルする」という事を表します。
先ほどの具体例で言うと50【Hz】の振動数のもとでは1秒間に50サイクルですから、
1サイクルあたりの時間(=周期)は0.02【s】です。
その時間あたりに1サイクルするという関係式が
0.02【s】×50【/s】=1というわけです。
振動数は、波の速さと波長との関係f=v/λもあります。意味は「1秒間に進む距離は何波長分か」という事で、それは1秒間あたりに何サイクルしているかに等しくなるわけです。
周期は振動数の逆数なのでT=λ/vとなります。これは1サイクルの波長に対して何秒で進行できるかを表し、それは1サイクルに要する時間である周期に等いというわけです。
また、後述する角周波数がω=2π/Tである事からT=2π/ωです。
その事はy=A sin(kx-ωt)の正弦波があった時に角周波数だけn倍したy=A sin(kx-nωt) は周期が1/n倍となっている事を意味します。
光や音波は一定の条件下で一定であるかほぼ一定とみなせるので、
その場合は振動数と波長は反比例の関係にあります。
光や音波の性質は振動数で大きく決まります。紫外線などの光や「高い音」は振動数が大きくて波長が短く、逆に赤外線などの光や「低い音」は振動数が小さくて波長が長い波動となっています。
可視光で言うと紫色の振動数が大きく、青、緑、黄色と小さくなって赤が振動数が一番小さい領域です。波長では逆に赤のほうが紫よりも大きくなります。
さらにより詳しく見ると一般的に振動数が高い波動ほどエネルギーが高く、紫外線などの振動数が高い光はエネルギーが高い光でもあります。
正弦波の波長
波の波長は基本的には時刻を固定した時の、
進行方向に対する「1周期分の波の長さ」を測ったものと言えます。
位置や距離を位相に換算する波数がk=2π/λで表され、
位置座標に由来する位相の部分はkxで表されます。
1周期分の距離(=波長)は2πに換算されます。
波長の1/2の「半波長」であればπに換算されるという計算です。
ただし時間を動かした時にも波長を考える計算はできます。
例えば波の進行の速さが200【m/s】である時、
1周期が0.1秒であるなら「1秒間に200メートル」は1秒が10周期分です。
つまりこの時、1周期分の0.1秒あたりは20メートルの進行があります。
さらに波の振動方向も見るとその間に1サイクルの振動が完了しているわけで、
進行方向の長さは波長です。
これは200【m/s】×0.1【s】=20【m】という計算です。
もし1周期が4秒だったら、波長は200【m/s】×4【s】=800【m】です。
これらの計算が「波長、速さ、周期の関係」を表すλ=vTの関係の意味です。
周期の代わりに振動数を使えばλ=v/fの関係になります。
もし光のように一定条件下で速さが常に一定であると考えられる場合にはλ=cTであり、波長と周期は比例関係にあります。(cは非常に大きい値なので短い周期でも波長は長くなり得ます。)
波の波長は、波同士を重ね合わせた時の波の干渉を分析する時に重要な量です。同じ物理量で表される2つの波が微妙に位相がずれた状態で重ね合わさると、波長の整数倍だけずれていると波は強め合い、波長の整数倍に半波長が加わると弱め合うという現象が起きます。
光が波動であるという実験的な根拠は、光に対して波の干渉が起きるという事(ヤングによる実験)です。(光は同時に粒子でもあります。その粒子が多数集まった時に波動性を表すようになります。ただし粒子同士が相互作用して波になっているという事では無く、より量子力学的な現象としてです。マクロなスケールでは光の波動性は電磁波としても扱われます。)
正弦波の速さ
波動が生じている時、
媒質は各位置で上下に振動しているだけだったとしても
見た目は波形が横に進行していくようにも見えます。
波の速さとは、そのような「波形が移動していく速さ」を指します。
波長および周期との関係式があり、λ=vTおよびλ=v/fが成立します。
そのため、質量を持った媒質の一部分に対して運動方程式を考えるような時には加速度はあくまで媒質の変位方向(波の進行方向に対して垂直方向など)を考える必要がある場合もあります。
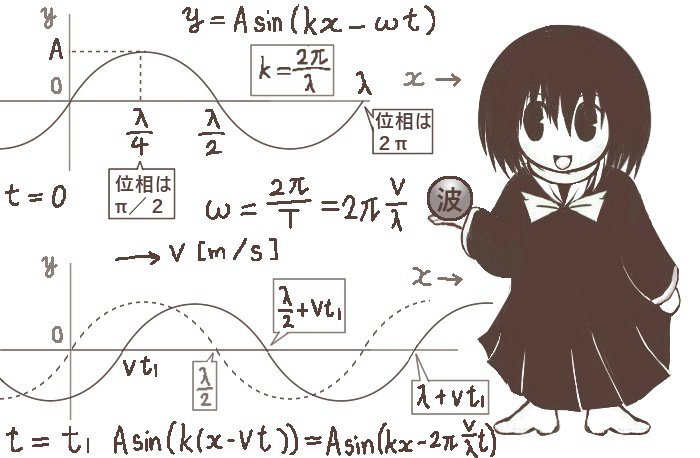
時刻がt=0の時に波形がy=A sin(kx)で表されている正弦波が、
速さvでx軸方向に移動しているとすると
一般の時刻tではy=A sin{k(x―vt)}=A sin{2π(x/λ―vt/λ)}で表されます。
【sin(kx-vt)ではない事に注意。vtメートル進むのはx軸での距離です。】
しかし正弦波の基本形はy=A sin(kx―ωt)であったはずです。
すると速さを考える時にはそれとは違った形になってしまうのか?というと、実はそうでは無く
ω=2π/T=2πv/λによりωt=2πvt/λとなるので、
A sin{k(x―vt)}=A sin (kx―ωt)の関係があります。
もう少し詳しく見ると波動において進行方向の速さがvであるという事は、
1つの時刻を固定した時に(例えばt=t0と指定)
xを変数とする2つの関数f(x)とg(x)があって、
f(x)=g(x+vt)が任意の位置xと時間tに対して成立する事を指します。
この関係式は「波がvt【m】進行した」という事を見やすい式です。
しかし、ではその時にy=g(x)はどのような関数形かというと、
x=X+vtとおくと、f(X)=g(X+vt)ですが
X=x-vtなのでf(x-vt)=g(x)であり、
「y=f(x)をx軸方向にpだけ平行移動した関数y=g(x)はg(x)=f(x-p)で表される」
という関数とグラフ上の平行移動についての一般的な関係式が得られます。
図形的にも物理的にも、y=Asin(kx)の波形全体がx軸のプラス方向に移動する時には
まず最初にx=0の位置においてyの値は小さくなっていきます。
関数は正弦関数ですから位相の値も0の状態からまず小さくなっていくわけで、
y=Asin(kxーωt)におけるーωtの項の意味を表しています。
ある正弦波y=A sin(kx―ωt)があってその進行方向を進行波として基準に考える時、同じ波形と物理量を持って「進行の向きだけが逆向き」の波はy=A sin(kx+ωt)で表され、反射波と呼ばれます。(物理的に見て、そのような波は多くの場合にどこかの端で反射して戻ってくるものなので。)
反射波のほうの式をvを使って書く事を考えると、
ここでは後述するω=kvの関係式を使う事にして
y=A sin(kx+ωt)=A sin(kx+vkt)=A sin {k(x+vt) } であり、
y=A sin(kx) の波形全体を「x軸のマイナス方向にvtだけ平行移動させた関数」に一致します。
角周波数
角周波数あるいは角振動数ωは、ωtの形で位相の時間部分を表す量です。
「角速度」(angular velocity)は回転運動を表すのに使う量ですが1秒間あたりの角度の変化量という意味では角周波数と同じであり、記号も同じωを使う事が多いです。
ただし角速度は波動以外の一般の運動に対して使う量ですから、波動における関係式は一般的には成立しません。
ω=2π/Tは、1周期分の時間で位相がπになるようにする換算の計算です。
例えばある時刻から0.5周期分だけの時間が経っているなら位相の変化(「位相差」)は
ωt=(2π/T)×0.5T=πとなる計算です。
ω=2πfの関係式も成立します。
例えば50【Hz】の振動数に対しては1秒間あたり100πの位相差が生じる事を意味します。
(※ただしその場合は100πは2πの整数倍ですから位置を固定すれば正弦関数の値は変化せず、実質の位相差は0と同じです。)
0.01秒間ではωt=2πft=100π×0.01=πの位相差が生じる計算になります。
基本となるA sin (kx―ωt)の形を見ると波数kと角周波数ωは一見全く別々の物理量かとも思えるわけですが、速さvによってkとωの関係式を作れます。
k=2π/λで、ω=2π/T=2πv/λなのでω=kvの関係が実はある事が分かります。
時刻を固定してから波の進行を考えてA sin (kx-ωt)の形を導出できるのと同様に、最初に位置を固定して時間による振動から考える事もできます。
t=0の時にx方向に関してはsin (kx)の波形があるとします。
この時に波がプラス方向に進行する時にはy方向の変位はx=0においてマイナス方向に現れ始めるので、敢えて「x=0でA sin (-ωt)の振動がある」と考えます。
プラスの値のxの位置で
「x=0の時と同じyの変位が現れる時刻」は波の速さを考慮してx/v秒後です。
よって、任意のxの位置における振動はω=kvの関係式も使って
y=A sin {-ω(t-x/v)}=A sin (-ωt+ωx/v)=A sin (kx―ωt)の形を得ます。
波数と平面や空間での波数ベクトル
波数はk=2π/λで表され、速さvを使うとk=2π/(vT)=ω/vとも表せます。
いずれにしても意味としては
「1波長分(1周期分)がいくつ含まれているかを位相に換算する量」という事になります。
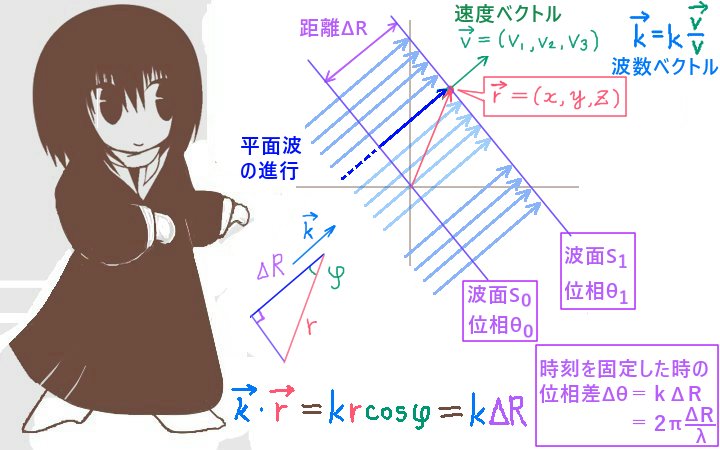
平面や空間では、波の進行方向を表すベクトルとして波数ベクトルが使われる事があります。
波数ベクトルの表し方はいくつかありますが、
その1つは個々の位置での波の進行についての速度ベクトルを使う方法です。
速度ベクトルを(v1,v2,v3)として、その大きさ(速さ)をvとします。
すると、速度ベクトルを「大きさが1である」単位ベクトルにした
(1/v) (v1,v2,v3)というベクトルを考えると
これは各点において波の進行方向を向く単位ベクトルです。
それにkを乗じたものを波数ベクトルとして考える事ができます。
すなわち、\(\overrightarrow{k}\)=(k/v) (v1,v2,v3)として考えます。
波数ベクトルの大きさは波数kに等しくなります。
特に平面波では同じ位相の平面が波を作っており
それらの平面間の距離によって位相差が決まるので、
原点から個々の点(x,y,z)から波の進行方向への射影を図形的に考えると距離の変化による位相の変化は波数ベクトルとベクトル(x,y,z)の内積で表す事ができます。
【原点を通る波面は必ず存在し、平面波においてその波面上での位相は等しいので統一的に波面と波面の位相差を「距離に波数kを乗じる」という式で表す事ができて、さらにそれは波数ベクトルを使うと内積により表現可能であるという事です。】
波の進行についての各点での速度ベクトルを\(\large{\overrightarrow{v}=(v_x,v_y,v_z)}\)として、
その大きさをvとすると
波数ベクトルは次式で表されます。
$$\overrightarrow{k}=k\frac{\overrightarrow{v}}{v}$$
$$\left|\overrightarrow{k}\right|=k=\frac{2\pi}{\lambda}$$
■特に空間内の平面波において各点の変位 u(x,y,z,t) を正弦波で表せる場合には、
\(\large{\overrightarrow{r}=(x,y,z)}\)として次式が成立します。
$$u(x,y,z,t)=A\sin\left(\overrightarrow{k}\cdot\overrightarrow{r}-\omega t\right)$$
ωtの部分は進行方向が1次元の場合と同じです。
また、平面波であれば実は正弦波でなくても
より一般的に
\(u(x,y,z,t)=f\left(\overrightarrow{k}\cdot\overrightarrow{r}-\omega t\right)\)と表す事が可能です。
波を正弦ではなく余弦で表す事と「位相のずれ」の関係
ところで正弦波を通常の三角関数として考えた時に、正弦ではなくて余弦で表してもよいのではないか?と思われるかもしれませんが、実際その通りで正弦波で表される波は余弦関数で表しても何ら支障はありません。
つまりy=A cos (kx―ωt)として波を表してもよいわけです。
ただし同じ物理量の波を正弦波で表した場合との関係には注意するべきで、
y=A cos (kx―ωt)=A sin (kx―ωt+π/2)の関係があります。
y=A sin (kx―ωt)とy=A cos (kx―ωt)との間には位相差があって、2つの関数を同時に使う時は正弦と余弦の関係からも分かるように同一の関数ではありません。
また同様に、正弦波をy=A sin (kx―ωt)ではなくy=A sin (ωt―kx)で表したとしてもそれ自体は波動の現象を考察するうえで基本的に問題は無いわけですが、やはり同じくy=A sin (kx―ωt)の波とは位相のずれがあり、
y=A sin (ωt―kx)=A sin (kx―ωt+π)=の関係があります。
今度は位相のずれはπになっているわけです。
【+πを-πとしても同じです。三角関数は2πを周期とするためです。
y=A sin (ωt―kx)=―A sin (kx―ωt)に等しいと見る事もできます。】
y=A sin (kx―ωt)は、より正確には定数θ0を使って
y=A sin (kx―ωt+θ0)の正弦波でθ0=0としたものです。
【通常はそれで問題は起きません。】
x=0,t=0の時の値がy=A sinθ0となります。
そしてそのθ0は必要があればπ/2でもπでもよいわけで、
そのような場合には波はy=A sin (kx―ωt+θ0)は
A cos (kx―ωt)やA sin (ωt―kx)に直接的に変形できます。
言い換えるとx=0,t=0の時のy=A sinθ0の値の設定次第で、
あるいは現に存在する波に対して
「進行方向のどこを原点にとっていつを時刻t=0に設定するか」により
A sin (kx―ωt),A cos (kx―ωt),A sin (ωt―kx)の形は実は自由に選べるわけです。

k=2π/λなのでkx-ωt+π/2=k(x+λ/4)-ωtとなり、
x軸のマイナス方向にλ/4【波長の1/4】だけもとの波形を平行移動させた形になっています。
正弦波の位相にπを加えた時は、同様にして
x軸のマイナス方向にλ/2だけもとの波形を平行移動させた形になっています。
正弦波の位相の表し方の整理
正弦波y=A sin (kx―ωt)において位相の形kx―ωtを見ると、位置座標と時刻の両方が変数になっています。つまり、同じ位置で時間による変動を見てもよいし、時刻を固定して波形の様子を見る事もできるようになっています。
つまり、いずれにしても位相に対する正弦関数の値として統一的に波の様子を表現できるようになっているわけです。
この事は、時刻を固定してx軸とy軸の関係でグラフを正弦関数として描けるだけでなく、位置xを固定して時刻tとy軸の関係におけるグラフも同じく正弦関数として描ける事を意味します。なぜならばどちらを変数としても、もう片方を固定すればy=A sin θの形の関数になっているためです。
正弦波の位相部分に対してはk=2π/λ,ω=2π/Tの関係を使って
y=A sin (kx―ωt)=A sin {2π(x/λ―t/T)}のように書く事もできます。
これは関係式を使って書き直しただけと言う事もできますが、
「位置や距離が波長の何倍か」「時刻や時間が周期の何倍か」で位相の変化を考えている事をより明確にするならこのようになるという事です。
もちろん、同じ意味をより簡潔に記せばy=A sin (kx―ωt)であるわけです。
さらに振動数fなどを使って書く事もできて、整理すると次のようになります。
| 使用する物理量の例 | 正弦波の位相 | 備考 |
| k,ω | kx―ωt | 基本形【ωt-kxでも可】 |
| λ,T | 2π(x/λ―t/T) | 位置は波長の何倍か、 時間は周期の何倍かで位相を見る |
| λ,f | 2π(x/λ―ft) | 時間を2πが何個分かで見る |
| v,T,λ | 2π{x/(vT)―vt/λ } | λ/v=Tよりλ=vT, 1/T=v/λ |
| k,v | k(x―vt) | x軸方向にvt平行移動した形 【kx―ωtに等しい】 |
| ω,t | ω(x/v-t) | x=0での振動から考えるか、 ω=kvの関係から |
単位を利用した関係式の理解の仕方【次元解析】
波動に関する物理量の関係式は基本的ないくつかの式(T=1/fなど)を除くとそもそも覚え込むような性質のものではありませんが、それにしても分母と分子の関係がごっちゃになったりする事もあるかもしれません。微積分の計算等とはまた違った難しさがあると言えます。
そこで、あくまで補助的なものである事は強調されるべきかと思いますが、単位の関係を利用して理解に役立てたり、関係式を思い出す際に混乱した時などに使える事があります。
(物理では「次元解析」とも言います。この「次元」とは平面を2次元、空間を3次元と呼んだりする「次元」とは直接的には無関係です。)
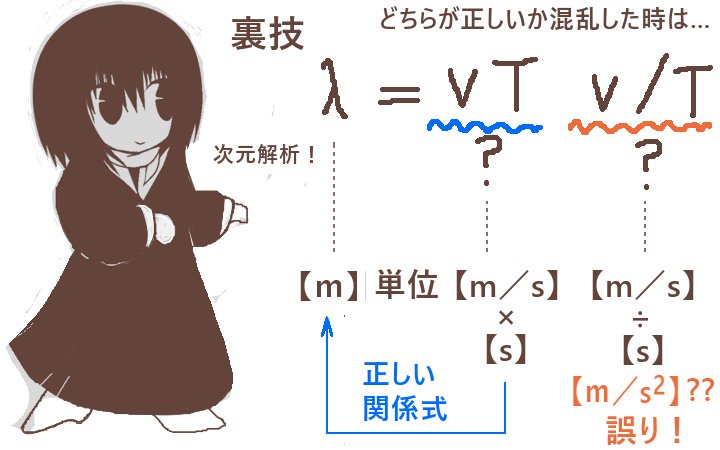
例えばλ,v,Tの関係を考えてみましょう。
これらの単位はそれぞれ【m】【m/s】【s】です。
すると、もし例えばλvとかv/Tといった値を考えるとそれらの単位は【m2/s】とか【m/s2】(後者は加速度の単位)といったものになってしまいますが、いずれもλ,v,Tの単位に該当せず、波動に関する他の物理量の単位にも当てはまりません。
すなわちλvとかv/Tといった量は少なくとも基本関係式で使う事は無いという判断が可能であるとも言えるわけです。
もし関係式を忘れてしまって必要なのに急に思い出せないとして、
単位の関係からλ,v,Tに対して成立する正しい関係式を推測するとしましょう。
すると、【m】と【s】から【m/s】が作れるはずであり、
λ【m】/T【s】=v【m/s】の関係が推測できます。実際、それは正しい関係式になっています。
同じように単位の関係だけからT【s】=λ【m】/v【m/s】の式を推測しても
実際にT=λ/vは正しい関係式です。
続いて、λ【m】=v【m/s】T【s】の推測からもλ=vTも正しい関係式を得ます。
λ=vTの式の右辺についてvTなのかv/Tなのか混乱した時には
単位として【m】となる前者が正しく、
【m/s2】すなわち加速度の単位になる後者は波長λを表す量としてあり得ない事を判定できます。
同様に、前述の波動に関する物理量の関係式は単位の関係からも理解可能です。
(下表で、振動数の単位は【Hz】ではなく【/s】で書いています。)
| 物理量 | 関係式 | 次元解析による理解の補助 |
| 周期 | T=1/f T=λ/v | 【s】=1/【/s】 【m】/【m/s】=【s】 |
| 波長 | λ=vT λ=v/f | 【m】=【m/s】・【s】 【m】=【m/s】/【/s】 |
| 振動数 | f=1/T f=v/λ | 【/s】=1/【s】 【/s】=【m/s】/【m】 |
| 速さ | v=λ/T v=λf | 【m/s】=【m】/【s】 【m/s】=【m】・【/s】 |
| 波数 | k=2π/λ k=2π/(vT) k=ω/v | 【rad/m】を基本形として、 【rad/m】=【rad】/(【m/s】・【s】) 【rad/m】=【rad/s】/【m/s】 |
| 角周波数 | ω=2πf ω=2π/T ω=kv | 【rad/s】を基本形として、 【rad/s】=【rad】/【s】 【rad/s】=【rad/m】・【m/s】 |
このような関係は単に式を覚えやすくなるという事に留まらず、物理学一般において異なる物理量の関係を調べる時に整合性がとれてるかの確認等を含めて考察の対象になる事があります。
また、物理量の単位というのは「1秒当たりに何メートル進むか」を【m/s】で表すといったように、それ自体に物理的な意味が含まれている事もあると言えます。
λ=vTの関係では速さに時間を乗じているから距離となるわけで、
そこに波動現象に特有の1サイクルあたりという意味が加味されるわけです。
物理的な意味(図的な意味も含めて)や数式的な意味に加えて、単位を使った理解の仕方も補助的に知っておくと便利な事があります。
波動方程式の解としての正弦波
一般的に、波動を表す式は次の波動方程式の解として得られます。
u(x,y,z,t)に対する次の微分方程式は波動方程式と呼ばれます。
$$\nabla^2u=\frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}$$
$$\nabla^2=\frac{\partial^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}+\frac{\partial^2 }{\partial z^2}$$
右辺の定数項の分母でvの文字を使っていますが、
実は波動方程式の解から得られる波動の速さはこの式中のvで表されます。
▽の記号はナブラと言います。
正弦波の式は1次元の場合の波動方程式の解の1つとなっています。
【ただし解の「1つ」であって、解の全て(一般解)ではありません。】
1次元の場合は関数に対するyの偏微分、zの偏微分は0であるとして波動方程式は、
対象の関数をy=y(x,t)を使って次式になります。
$$\frac{\partial^2 y}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 y}{\partial t^2}$$
y=Asin(kx-ωt)がこの式の解であるかどうかは実際に偏微分を行う形で確認できます。
合成関数の微分(1変数)に注意して計算をまとめると次のようになります。
| y=Asin(kxーωt) | xによる偏微分 | tによる偏微分 |
| 偏微分1回目 | kAcos(kx-ωt) | -ωAcos(kx-ωt) |
| 偏微分2回目 | -k2Asin(kx-ωt) | -ω2Asin(kx-ωt) |
tによる偏微分の2回目では、cos の微分由来のマイナスと-ωtの微分由来のマイナスの2つが乗じられるので結果的に符号は1回目の偏微分の時から変わらない事になります。
∂2y/∂x2と∂y2/∂t2の計算結果を見比べてみると、
∂2y/∂x2=(k/ω)2(∂y2/∂t2) となっています。
つまり、v=ω/k であると考えると確かに上記の波動方程式を満たしています。
さらに、波の関係式においてω=vkでしたから波動方程式を満たす定数としての
v=ω/kは正弦波の進行の速さのvと同一の量である事を確認できます。